CFA - Как рассчитывать будущую стоимость денежного потока (FV)?
Рассмотрим временную стоимость денег (TVM) единичного потока денежных средств, а также порядок расчета будущей стоимости (FV) при различных способах начисления процентов.
Существует взаимосвязь между первоначальной инвестицией (PV), которая приносит доход по процентной ставке \(r\) за период, и будущей стоимостью (FV) этой инвестиции, которая будет получена через \(N\) лет или периодов.
Следующий пример иллюстрирует эту концепцию FV.
Предположим, вы вкладываете $100 (PV = 100) на депозитный банковский счет, который приносит доход 5% в год.
В конце 1 года вы получите $100 плюс проценты, рассчитываемые как 0,05 \(\times\) 100 = $5, что в общей сложности составляет $105.
Чтобы формализовать этот пример расчета FV за 1 период, мы определяем следующие термины:
- \(\large \PV\)= текущая или приведенная стоимость инвестиций (англ. 'present value').
- \(\large \FV_N\) = будущая стоимость инвестиций через \(N\) периодов от текущей даты (англ. 'future value').
- \(r\) = процентная ставка за период.
Для \(N = 1\) формула для расчета будущей стоимости PV будет такой:
\( \dstL \FV_1 = PV (1 + r) \) (Формула 1)
В нашем примере мы вычисляем будущую стоимость через 1 год от текущей даты:
\( \FV_1 = $100 (1.05) = $105 \)
Теперь предположим, что вы решили инвестировать первоначальные $100 на 2 года с учетом суммы процентов, начисляющихся на ваш счет ежегодно (т.е. при ежегодном начислении сложных процентов).
В конце 1 года (на начало 2 года) на вашем счете будет $105, которые вы оставите в банке еще на год. Таким образом, при начальном размере инвестиций в $105 (PV = 105), сумма на конец второго года составит:
$105(1,05) = $110,25
Обратите внимание, что проценты в размере $5,25, полученные за 2 год, составляют 5% от суммы, оставшейся на банковском счете на начало 2 года.
Еще один способ понять этот пример - отметить, что сумма, вложенная в начале 2-го года, состоит из первоначальной суммы в $100 плюс проценты $5, заработанные в течение 1-го года. В течение 2-го года первоначальная сумма вклада снова приносит проценты, а также проценты от процентов, которые были заработаны за 1-й год.
В приведенной ниже таблице вы более наглядно можете увидеть, как растут первоначальные инвестиции:
|
Первоначальные инвестиции |
$100 |
|
Проценты за 1 год ($100 \(\times\) 0.05) |
5 |
|
Проценты за 2 год от первоначальных инвестиций (100 \(\times\) 0,05) |
5 |
|
Проценты за 2 год от процентов, полученных за 1 год (0,05 \(\times\) 5) |
0,25 |
|
Итого |
$110,25 |
Процентный доход в размере $5, полученный за каждый период от первоначальных инвестиций в размере $100, известен как простой процент (англ. 'simple interest'): процентная ставка, умноженная на основную сумму.
Основная сумма (англ. 'principal') - это сумма первоначально вложенных средств.
В течение двухлетнего периода вы получаете простые проценты в размере $10. Дополнительные $0,25, которые у вас образовались в конце 2 года, - это проценты, начисленные на сумму процентов в $5, которую вы заработали за 1 год и реинвестировали.
Проценты, полученные по процентам в этом примере, дают представление о явлении, которое известно как компаундинг или наращение или капитализация процентов или просто начисление сложного процента (англ. 'compounding').
Сложный процент, полученный от реинвестирования процентов, обеспечивает сильный эффект наращения инвестиций, потому что при заданной процентной ставке сумма процентов растет в каждом периоде.
Эффект наращения процентов усиливается с ростом величины процентной ставки. Например, $100, вложенные сегодня, стоили бы около $13,150 через 100 лет при начислении сложного процента по ставке 5%, но они также стоили бы более $20 млн. за тот же период при ставке 13%.
Чтобы проверить это, нам нужна общая формула, позволяющая рассчитать сложный процент для любого количества периодов. Следующая общая формула связывает текущую стоимость первоначальных инвестиций с их будущей стоимостью через \(N\) периодов:
\( \dstL \FV_N = \PV (1 + r)^N \) (Формула 2)
где
- \(r\) - процентная ставка за период, а
- \(N\) - количество периодов наращения процентов.
В примере с банком расчет будет таким:
\( FV_2 = $100 (1 + 0,05)^2 = $110,25 \)
В примере с инвестициями по ставке 13%:
\( FV_{100} = $100 (1.13)^{100} = $20,316,287.42 \)
Наиболее важным моментом, о котором следует помнить при использовании формулы будущей стоимости денежного потока FV, является то, что процентная ставка r и количество периодов наращения \(N\) должны соответствовать общему временному периоду. То есть, обе эти переменные должны быть определены в одних и тех же единицах времени.
Например, если \(N\) указана в месяцах, тогда r должна быть 1-месячной процентной ставкой.
Временная линия помогает нам отслеживать соответствие единиц времени процентной ставки и периодов. На графике временной линии мы используем знак \(t\), чтобы отметить момент начала / окончания периода. Он также обозначает номер (индекс) определенного периода.
Таким образом, текущая стоимость PV представляет собой сумму, которую можно инвестировать в текущую дату с номером \(t\) = 0. Мы можем ссылаться на момент окончания инвестиционного периода (срок возврата средств) как на \(t = N\).
Временная линия на рисунке ниже показывает эту связь.
 Связь между первоначальными инвестициями PV и их будущей стоимостью FV.
Связь между первоначальными инвестициями PV и их будущей стоимостью FV.
На графике ниже первоначальные инвестиции PV отражены в периоде t = 0. Используя Формулу 2, мы перемещаем текущее значение PV вперед, к периоду \(t = N\), с помощью коэффициента \((1 + r)^N \).
Этот коэффициент называется фактором будущей стоимости (англ. 'future value factor').
Обозначим будущую стоимость на временной линии как FV и расположим ее в точке \(t = N\). Предположим, что будущее значение должно быть получено ровно через 10 периодов от текущей даты (\(N\) = 10).
Текущая стоимость PV и будущая стоимость FV разделены во времени через коэффициент \((1 + r)^{10} \).
Тот факт, что текущая (приведенная) стоимость и будущая стоимость разделены во времени, имеет важные последствия:
- Мы можем добавлять суммы денег только в том случае, если они индексируются в тот же момент времени.
- При заданной процентной ставке \(r\), будущая стоимость FV увеличивается с ростом количества периодов \(N\).
- Для данного количества периодов \(N\), будущая стоимость FV увеличивается с ростом процентной ставки \(r\).
Чтобы лучше понять эти концепции, рассмотрим три примера, иллюстрирующих применение формулы будущей стоимости.
Пример (1) расчета будущей стоимости FV с реинвестированием процентов по той же процентной ставке.
Допустим, вы - счастливый победитель лотереи с призом в размере $5 млн. после уплаты налогов. Вы инвестируете свой выигрыш в 5-летний депозитный сертификат (CD) в местном банке. CD обещает ежегодную выплату по годовой процентной ставке 7%.
Это банк также позволяет реинвестировать проценты по той же процентной ставке в течение срока действия депозитного сертификата.
Какую сумму вы заработаете через 5 лет, если будете реинвестировать начисленные проценты по ставке 7% в течение пяти лет?
Решение:
Вычислим будущую стоимость инвестиций FV, используя в формуле следующие значения в:
\(\PV\) = $5,000,000
\(r\) = 7% = 0.07
\(N\) = 5
\( \begin{aligned}
\FV_N &= \PV (1 + r)^N \\[1ex]
&= $5,000,000 (1.07)^5 \\
&= $5,000,000 (1.402552) \\
&= $7,012,758.65
\end{aligned} \)
По истечении 5 лет у вас будет $7,012,758.65.
Обратите внимание, что фактор будущей стоимости округлен до шести десятичных знаков после нуля, но расчет может фактически отражать большую точность.
Например, фактор будущей стоимости в примере 1.402552 был округлен от 1.40255173, но расчет фактически выполняется (калькулятором или электронной таблицей) с фактором более 8 десятичных знаков после нуля.
Пример (2) расчета будущей стоимости FV без реинвестирования процентов.
Финансовая организация предлагает вам следующие условия: за инвестиции в размере ¥2,500,000 компания обещает выплатить вам единовременную сумму через 6 лет по годовой процентной ставке 8%.
Какова будет будущая стоимость инвестиций?
Решение:
Используйте следующие данные в Формуле 2, чтобы найти будущую стоимость FV:
\(\PV\) = ¥2,500,000
\(r\) = 8% = 0.08
\(N\) = 6
\( \begin{aligned}
\FV_N &= \PV (1 + r)^N \\[1ex]
&= ¥2,500,000 (1.08)^6 \\
&= ¥2,500,000 (1.586874) \\
&= ¥3,967,186
\end{aligned} \)
Через 6 лет вы получите ¥3,967,186.
Наш третий пример - более сложная задача расчета FV, которая иллюстрирует важность отслеживания фактических календарных сроков.
Пример (3) расчета будущей стоимости с отсроченной единовременной инвестицией.
Менеджер пенсионного фонда ожидает, что его корпоративный клиент внесет $10 млн. через 5 лет от текущей даты. Норма прибыли активов фонда оценивается в 9% годовых.
Менеджер пенсионного фонда хочет рассчитать будущую стоимость этого взноса через 15 лет от текущей даты, то есть на дату, когда средства будут распределены пенсионерам.
Какой будет будущая стоимость?
Решение:
При индексе периода \(t = 5\) мы можем рассчитать будущую стоимость вклада, используя следующие данные в Формуле 2:
\(\PV\) = $10,000,000
\(r\) = 9% = 0.09
\(N\) = 10
\( \begin{aligned}
\FV_N &= \PV (1 + r)^N \\[1ex]
&= $10,000,000 (1.09)^{10} \\
&= $10,000,000 (2.367364) \\
&= $23,673,636.75
\end{aligned} \)
Эта задача очень похожа на предыдущие две, но есть одно важное отличие: временная линия инвестиций.
С текущей даты \((t = 0)\) будущая стоимость через 15 лет составит $23 673 636,75.
Хотя будущая стоимость FV соответствует 10-летнему сроку начисления процентов, первоначальная стоимость в $10 млн. будет получена только через 5 лет от текущей даты.
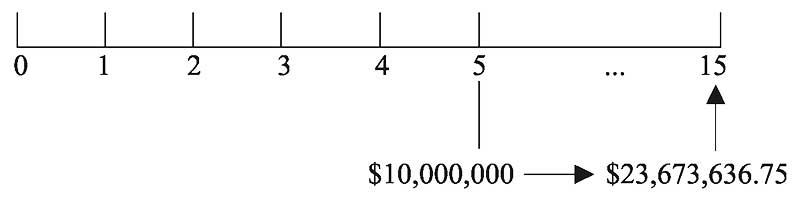 Будущая стоимость (FV) при первоначальной инвестиции t ≠ 0.
Будущая стоимость (FV) при первоначальной инвестиции t ≠ 0.
Как показано на графике выше, первоначальные инвестиции в размере $10 млн. должны быть осуществлены через 5 лет, поэтому эта сумма индексируется как \(t = 5\) и отображается на временной линии в соответствующей точке.
Будущая стоимость инвестиций FV через 10 лет индексируется как \(t\) = 15, то есть 10 + 5.
Временные линии, подобные приведенной выше, могут быть чрезвычайно полезными при решении более сложных задач, особенно тех, которые связаны с несколькими потоками денежных средств.
Предположим, что менеджер пенсионного фонда также должен получить сегодня от корпоративного клиента $6,499,313,86.
Сколько будет стоить эта сумма через 5 лет?
Сколько она будет стоить через 15 лет?
\(\PV\) = $6,499,313.86
\(r\) = 9% = 0.09
\(N\) = 5
\( \begin{aligned}
\FV_N &= \PV (1 + r)^N \\[1ex]
&= $6,499,313.86 (1.09)^5 \\
&= $6,499,313.86 (1.538624) \\
&= $10,000,000 \text{ через 5 лет}
\end{aligned} \)
А также:
\(\PV\) = $6,499,313.86
\(r\) = 9% = 0.09
\(N\) = 15
\( \begin{aligned}
\FV_N &= \PV (1 + r)^N \\[1ex]
&= $6,499,313.86 (1.09)^{15} \\
&= $6,499,313.86 (3.642482) \\
&= $23,673,636.74 \text{ через 15 лет}
\end{aligned} \)
Частота начисления процентов.
Рассмотрим инвестиции, для которых проценты выплачиваются более одного раза в год, т.е. инвестиции с разной частотой начисления процентов (англ. 'compounding frequency').
Например, многие банки предлагают ежемесячную процентную ставку, которая начисляется 12 раз в год. По такому вкладу банки начисляют проценты на проценты каждый месяц.
Вместо того, чтобы указывать периодическую ежемесячную процентную ставку, финансовые учреждения часто ссылаются на годовую процентную ставку, которую мы называем заявленной годовой процентной ставкой (англ. 'stated annual interest rate') или котируемой процентной ставкой (англ. 'quoted interest rate').
Заявленная годовая процентная ставка обозначается в формулах как rS. Заявленная годовая процентная ставка равна месячной процентной ставке, умноженной на 12.
Например, ваш банк может заявить, что за определенный депозит он платит 8% ежемесячно. В этом случае месячная процентная ставка составляет 0,08 / 12 = 0,0067 или 0,67%.
Эта ставка является сугубо ориентировочным значением, поскольку \((1 + 0,0067)^{12} = 1,083\), а не 1.08. Значение \((1 + r_s)\) не является фактором будущей стоимости для расчета процентов за период меньше 1 года.
Формула будущей стоимости может быть выражена в виде более чем одного периода составления отчетности в год.
\( \dstL \FV_N = \PV \left(1 + {r_s \over m} \right)^{mN} \) (Формула 3)
где
- \(r_s\) - заявленная годовая процентная ставка,
- \(m\) - количество составляющих периодов года, a
- \(N\) - обозначает количество лет.
Обратите внимание на совместимость между заявленной процентной ставкой, периодической ставкой \(r_s / m\) и количеством периодов начисления \(mN\).
Периодическая ставка (англ. 'periodic rate') \(r_s / m\) представляет собой заявленную годовую процентную ставку, деленную на количество периодов начисления в году.
Общее количество периодов начисления \(mN\), представляет собой количество периодов начисления за 1 год, умноженное на количество лет.
Периодическая ставка \(r_s / m\) и количество периодов начисления \(mN\) должны быть совместимыми.
Пример (4) расчета будущей стоимости FV с ежеквартальным начислением процентов.
Продолжая пример с депозитным сертификатом, предположим, что ваш банк предлагает вам депозит с 2-летним сроком. Заявленная годовая процентная ставка в размере 8% начисляется ежеквартально, а также есть возможность реинвестирования процентов по той же процентной ставке. Вы решили вложить $10,000.
Сколько будет стоить депозит к моменту его закрытия?
Решение:
Вычислим будущую стоимость с помощью Формулы 3 следующим образом:
\(\PV\) = $10,000
\(r_S\) = 8% = 0.08
\(m\) = 4
\(r_s / m\) = 0.08/4 = 0.02
\(N\) = 2
\(mN\) = 4(2) = 8 периодов начисления
\( \begin{aligned}
\FV_N &= \PV \left(1 + {r_s \over m} \right)^{mN} \\[1ex]
&= $10,000(1.02)^8 \\
&= $10,000(1.171659) = $11,716.59
\end{aligned} \)
К моменту закрытия депозит будет стоить $11,716.59.
Формула 3 не отличается от Формулы 2. Просто имейте в виду, что в ней используется периодическая процентная ставка, а экспонента - это общее количество периодов начисления.
Пример (5) расчета будущей стоимости FV с ежемесячным начислением процентов.
Банк предлагает вклад под 6% с ежемесячной выплатой начислений. Вы решили инвестировать $1 млн. на 1 год.
Какова будущая стоимость ваших инвестиций, если процентные платежи реинвестируются под 6%?
Решение:
Используя Формулу 3, найдем будущую стоимость инвестиции следующим образом:
\(\PV\) = $1,000,000
\(r_S\) = 6% = 0.06
\(m\) = 12
\(r_s / m\) = 0.06/12 = 0.005
\(N\) = 1
\(mN\) = 12(1) = 12 периодов начисления
\( \begin{aligned}
\FV_N &= \PV \left(1 + {r_s \over m} \right)^{mN} \\[1ex]
&= $1,000,000(1.005)^{12} \\
&= $1,000,000(1.061678) = $1,061,677.81
\end{aligned} \)
Если бы вам выплачивали 6% с годовым начислением, будущая стоимость составляла бы всего $1,000,000(1.06) = $1,060,000 вместо $1,061,677.81 при ежемесячном начислении.
Непрерывное начисление сложных процентов.
Приведенное выше обсуждение периодов начисления сложных процентов иллюстрирует дискретное начисление, связанное с расчетом процентов за определенный период времени.
Если количество периодов начисления в год становится бесконечным, то такое начисление процентов считается непрерывным.
Если мы хотим использовать формулу будущей стоимости FV с непрерывным начислением, нам нужно найти предельное значение фактора будущей стоимости для \(m \rightarrow \infty \) (т.е. бесконечно много периодов начисления в год) в Формуле 3.
Формула для будущей стоимости суммы через \(N\) лет с непрерывным начислением:
\( \dstL \FV_N = \PV e^{r_SN} \) (Формула 4)
Выражение \(e^{r_SN}\) является трансцендентальным числом \(e \approx 2,7182818\), возведенным в степень \(r_SN\). Большинство финансовых калькуляторов имеют функцию \(e^x\).
Пример (6) расчета будущей стоимости FV с непрерывным начислением процентов.
Предположим, что инвестиции в размере $10,000 будут приносить 8% годовых с непрерывным начислением в течение 2 лет.
Мы можем вычислить будущее значение с помощью Формулы 4 следующим образом:
\(\PV\) = $10,000
\(r_S\) = 8% = 0.08
\(N\) = 2
\( \begin{aligned}
\FV_N &= \PV e^{r_SN} \\
&= $10,000e^{0.08(2)} \\
&= $10,000(1.173511) = $11,735.11
\end{aligned} \)
При такой же процентной ставке, но с использованием непрерывного начисления инвестиции в размере $10,000 вырастут до $11,735,11 за два года по сравнению с $11,716,59 при ежеквартальном начислении, как показано в Примере 4.
В таблице ниже показано, как заявленная годовая процентная ставка в размере 8% генерирует разные суммы будущей стоимости при годовом, полугодовом, ежеквартальном, ежемесячном, ежедневном и непрерывном начислении для первоначальной инвестиции в размере $1 (с округлением результата до шести знаков после запятой).
Как видно из таблицы, все шесть вариантов начисления имеют одинаковую процентную ставку в 8%, но дают разные результаты из-за различий в частоте начисления процентов (англ. 'compounding frequency').
Более частое начисление приводит к увеличению итоговой будущей стоимости FV. Итоговая сумма при непрерывного начисления - это максимальный результат, который можно получить при заявленной годовой ставке 8%.
|
Частота |
\(r_s / m\) |
\(mN\) |
Будущая стоимость $1 |
|
|---|---|---|---|---|
|
Годовая |
8%/1 = 8% |
1 \(\times\) 1 = 1 |
$1.00 (1.08) |
=$1.08 |
|
Полугодовая |
8%/2 = 4% |
2 \(\times\) 1 = 2 |
$1.00 (1.04)2 |
=$1.081600 |
|
Квартальная |
8%/4 = 2% |
4 \(\times\) 1 = 4 |
$1.00 (1.02)4 |
=$1.082432 |
|
Ежемесячная |
8%/12 = 0.6667% |
12 \(\times\) 1 = 12 |
$1.00 (1.006667)12 |
=$1.083000 |
|
Ежедневная |
8%/365 = 0.0219% |
365 \(\times\) 1 = 365 |
$1.00 (1.000219)365 |
=$1.083278 |
|
Непрерывная |
$1.00 е0.08(1) |
=$1.083287 |
||
Из таблицы также видно, что доход от инвестиций в размере $1, по ставке 8,16% при годовом начислении даст такой же доход как ставка 8% при полугодовом начислении.
Этот результат приводит нас к различию между заявленной годовой процентной ставкой и эффективной годовой процентной ставкой (EAR, от англ. 'effective annual rate').
Для заявленной годовой процентной ставки в 8% с полугодовым начислением EAR составляет 8,16%.
Среди терминов, используемых для обозначения эффективной годовой доходности по процентным банковским депозитам, следует упомянуть:
- Годовую процентную доходность (APY от англ. 'annual percentage yield') используемую в США.
- Эквивалентную APY эффективную годовую процентную ставку (EAR, от англ. 'effective annual rate'), используемую в Великобритании.
- В отличие от APY и EAR, годовая процентная ставка (APR, от англ. 'annual percentage rate') измеряет стоимость заимствований и выражается годовой процентной ставкой.
В США APR рассчитывается как периодическая ставка, умноженная на количество периодов оплаты в год, в результате чего некоторые авторы используют APR в качестве общего синонима для заявленной годовой процентной ставки.
Тем не менее, APR - это термин с юридическим подтекстом. Расчет APR соответствует нормативным стандартам, которые меняются на международном уровне.
Поэтому «заявленная годовая процентная ставка» является предпочтительным общим термином для годовой процентной ставки в годовом исчислении, которая не учитывает промежуточные начисления в течение года.
Заявленные и эффективные процентные ставки.
Заявленная годовая процентная ставка не позволяет рассчитать будущую стоимость напрямую, поэтому для этого нам нужна формула EAR.
Для годовой процентной ставки 8, начисляемой раз в полгода, мы получаем периодическую ставку в 4% = (8% / 2).
В течение года инвестиции в размере $1 вырастут до $1 \(\times\) (1.04)2 = $1.0816, как показано в таблице выше. Проценты, полученные от инвестиций в размере $1, составляют $0,0816 и представляют собой эффективную годовую процентную ставку в размере 8,16%.
Эффективная годовая ставка рассчитывается следующим образом:
(Формула 5)
\(
\def\EAR{{\rm EAR}}
\dstL
\EAR = \left(1 + \stBfL{Периодическая}{процентная ставка} \right)^m - 1
\)
Периодическая процентная ставка (англ. 'periodic interest rate') представляет собой заявленную годовую процентную ставку, деленную на m, где m - количество периодов начисления в 1 году.
Используя предыдущий пример, мы можем рассчитать EAR следующим образом:
\( (1.04)^2 - 1 = 8,16\%\)
Cм. также примеры использования EAR в финансовых вычислениях.
Концепция EAR распространяется на непрерывное начисление процентов.
Предположим, что проценты по ставке 8% начисляются непрерывно. Мы можем вычислить EAR так же, как и выше, найдя соответствующий фактор будущей стоимости.
В этом случае инвестиции в $1 вырастут до:
\( $10,000e^{0.08(10)} = $1.0833 \)
Проценты, полученные за 1 год, представляет собой эффективную годовую ставку в 8,33%, что больше, чем EAR в 8,16% с полугодовым начислением, поскольку проценты начисляются чаще.
При непрерывном начислении мы можем рассчитать эффективную годовую ставку следующим образом:
\( \dstL {\rm EAR} = e^{r_S} -1 \) (Формула 6)
Мы можем изменить формулу для EAR с дискретным и непрерывным начислением, чтобы найти периодическую ставку, соответствующую конкретной эффективной годовой ставке.
Предположим, мы хотим найти соответствующую периодическую ставку для EAR 8,16% с полугодовым начислением.
Мы можем использовать Формулу 5 для расчета периодической ставки:
\(
\def\stav{{ \text{периодическая ставка}}}
\begin{aligned}
0,0816 &= (1 + \stav)^2 - 1 \\[1ex]
1.0816 &= (1 + \stav)^2 \\[1ex]
(1.0816)^{1/2} - 1 &= \stav \\[1ex]
(1,04) - 1 &= \stav \\[1ex]
4\% &= \stav
\end{aligned} \)
Чтобы рассчитать непрерывно начисляемую ставку (заявленную годовую процентная ставку с непрерывным начислением), соответствующую эффективной годовой ставке 8,33%, мы находим процентную ставку, которая удовлетворяет уравнению Формулы 6:
\( \begin{aligned}
0,0833 &= e^{r_S} - 1 \\[1ex]
1.0833 &= e^{r_S}
\end{aligned} \)
Для решения этого уравнения находим натуральный логарифм обеих сторон. Напомним, что натуральный логарифм \(e^{r_S}\) равен:
\( \ln e^{r_S} = r_S \)
Следовательно,
\( \ln 1.0833 = r_S \), а \(r_S\) = 8%.
Мы видим, что заявленная годовая ставка 8% с непрерывным начислением эквивалентна EAR в 8,33%.
Выше мы рассмотрели порядок расчета будущей стоимости для единичного денежного потока.
Для расчета серии денежных потоков см.:
CFA - Как рассчитывать будущую стоимость последовательности денежных потоков (аннуитет)?
