Как рассчитать размер платежей по ипотеке с фиксированной процентной ставкой?

Вы планируете приобрести дом стоимостью $120,000, сделав первоначальный взнос в размере $20,000 за счет собственных средств, а также заимствуя остаток суммы по 30-летней ипотеке с ежемесячными платежами по фиксированной процентной ставке.

Первый платеж по ипотеке должен быть осуществлен при \(t = 1\).

Текущая заявленная процентная ставка по ипотечному кредиту составляет 8% при ежемесячном начислении процентов.

Каковы будут ваши ежемесячные платежи по ипотечному кредиту?

Расчет:

Банк будет рассчитывать платежи по ипотечному кредиту таким образом, чтобы при указанной периодической процентной ставке текущая (приведенная) стоимость платежей PV была равна сумме заимствованных средств (в данном случае $100,000).

Имея это в виду, мы можем использовать Формулу 11

\( \dst \PV = A \left [1- \dst {1 \over (1 + r)^N} \over r \right] \)

чтобы рассчитать сумму аннуитетного платежа A.

Для этого необходимо разделить текущую (приведенную) стоимость PV на фактор текущей (приведенной) стоимости аннуитета:

\(\PV\) = $100,000
\(r_s\) = 8% = 0.08
\(m\) = 12
\(r_s / m\) = 0.08/12 = 0.006667
\( N\) = 30
\(mN\) = 12 \(\times\) 30 = 360

\( \dst \begin{aligned}
\stRmL{Фактор приведенной}{стоимости} &=
{1- \dst { 1 \over \left [1 + (r_s / m) r\right]^{mN} } \over r_s / m} \\[1ex]
&= {1- \dst {1 \over (1.006667)^{360} } \over 0.006667}
= 136.283494
\end{aligned} \)

\( \dst \begin{aligned}
A &= \PV \Big/ \stRml{Фактор приведенной}{стоимости} \\[1ex]
&= $100,000 / 136.283494 = $733.76
\end{aligned} \)

Сумма ипотеки в размере $100,000 эквивалентна 360 ежемесячным платежам в размере $733.76 при заявленной процентной ставке в 8%.

Расчет ипотеки - это относительно простая задача, связанная с определением размера аннуитетного платежа.

См. также:

CFA - Жилищные ипотечные кредиты.

Теперь перейдем к проблеме планирования выхода на пенсию.

Эта проблема иллюстрирует сложность ситуации, при которой человек хочет выйти на пенсию с определенным уровнем пенсионных сбережений.

В течение своей жизни обычный человек может сэкономить только небольшую сумму в начале своей карьеры, но в более зрелом возрасте у него обычно появляются более значительные финансовые ресурсы для увеличения пенсионных взносов.

Пенсионные планы часто связаны с неравномерными денежными потоками.

При работе с неравномерными денежными потоками мы максимально используем принцип, согласно которому стоимость денежных потоков, относящихся к одним и тем же моментам времени, является аддитивной - это называется принципом аддитивности денежных потоков.

Пример расчета суммы аннуитета, необходимой для финансирования будущих пенсионных сбережений.

Сейчас (при \(t = 0\)) Джилл Грант 22 года.

Она планирует выйти на пенсию в возрасте 63 лет (при \(t = 41\)).

Она также планирует откладывать на пенсию $2,000 в год в течение следующих 15 лет (с \(t = 1\) до \(t = 15\)).

В дальнейшем, в возрасте 40 лет, она начнет получать пенсионный доход в размере $100,000 в год в течение 20 лет, при этом первая пенсионная выплата начинается при \(t\) = 41.

Какую сумму Грант должна откладывать каждый год с t = 16 до t = 40 для достижения своей цели выхода на пенсию?

Предположим, что она планирует инвестировать в диверсифицированный паевой фонд акций и облигаций, который в среднем будет зарабатывать 8% в год.

Решение:

Чтобы решить эту проблему, мы изобразим известную нам информацию на временной линии.

Как показано на рисунке ниже, Грант будет откладывать $2,000 (отток денежных средств) ежегодно с 1 по 15 годы. Начиная с 41 года, Грант начнет получать пенсионный доход в размере $100,000 (приток денежных средств) в год в течение 20 лет.

На временной линии годовые пенсионные взносы записываются в круглых скобках как отрицательные суммы ($2), чтобы показать, что это отток денег.

Вопрос заключается в том, чтобы рассчитать сумму пенсионных взносов, отображенную на временной линии как X: с 16-го по 40-й год.

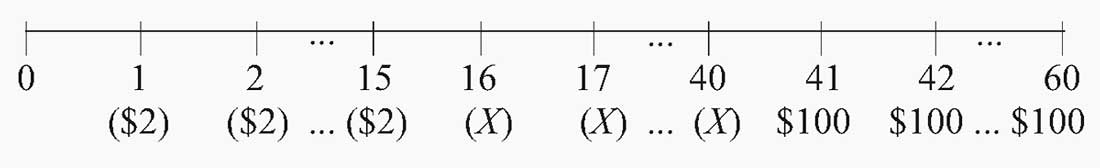Временная линия пенсионных аннуитетных платежей (в тыс.) Временная линия пенсионных аннуитетных платежей (в тыс.)

Решение этой задачи включает в себя соблюдение следующего равенства: текущая стоимость сбережений (оттоков денежных средств) равна текущей стоимости пенсионного дохода (притоков денежных средств).

Мы могли бы привести все денежные суммы к моменту \(t\) = 40 или к \(t\) = 15 и после этого найти \(X\).

Сначала рассчитаем приведенную стоимость всех денежных сумм при \(t\) = 15 (мы рекомендуем читателю решить эту задачу альтернативным способам, приведя все денежные потоки к моменту \(t\) = 40).

Начиная с \(t\) = 15, 1-ый платеж в сумме \(X\) будет осуществлен через 1 период (при \(t\) = 16). Таким образом, мы можем рассчитать \(X\), используя Формулу 11 приведенной (текущей) стоимости обычного аннуитета.

Данная задача включает три последовательные группы денежных потоков. Основная идея заключается в том, что текущая стоимость пенсионного дохода должна быть равна текущей стоимости пенсионных взносов Грант.

Решение этой задачи требует следующих шагов:

Шаг 1. Найдите будущую стоимость пенсионных взносов в размере $2,000 в год к моменту времени \(t\) = 15. Полученное значение говорит нам, какая сумма сбережений будет у Грант к этому моменту.

Шаг 2. Найдите текущую стоимость пенсионного дохода при \(t\) = 15. Это значение говорит нам, сколько денег Грант должна откладывать, начиная с момента \(t\) = 15, чтобы достичь своих пенсионных целей в дальнейшем.

Этот шаг включает 2 расчета.

  • Сначала вычислите текущую стоимость аннуитета в размере $100,000 в год при \(t\) = 40. Используйте формулу текущей стоимости аннуитета. Обратите внимание, что текущее значение соответствует моменту времени \(t\) = 40, потому что 1-й платеж равен \(t\) = 41.
  • Затем дисконтируйте полученную текущую стоимость к моменту \(t\) = 15 (за 25 периодов).

Шаг 3. Теперь вычислите разницу между суммой, которую Грант сэкономила на Шаге 1, и суммой, необходимой ей для достижения ее целей выхода на пенсию (Шаг 2).

Ее сбережения в период времени с \(t\) = 16 до \(t\) = 40 должны представлять собой приведенную стоимость, равную разнице между будущей стоимостью ее пенсионных взносов и текущей стоимостью ее пенсионного дохода.

Наша конечная цель - определить сумму, которую Грант должна откладывать в качестве пенсионного взноса в каждый из 25 лет, с \(t\) = 16 до \(t\) = 40.

Шаг 1.

Начнем с расчета будущей стоимости пенсионных взносов в размере $2,000 к моменту \(t\) = 15, а именно:

\(A\) = $2,000
\(r\) = 8% = 0.08
\(N\) = 15

Используем Формулу 7:

\( \dst \begin{aligned}
\FV_N &= A \left[ {(1+r)^N - 1}  \over r \right]  \\[1ex]
&= $2,000 \left[ {(1.08)^{15} - 1}  \over 0.08 \right] \\[1ex]
&= $2,000(27.152114) = $54,304.23
\end{aligned} \)

К моменту \(t\) = 15 первоначальные пенсионные сбережения Грант увеличатся до $54,304.23.

Шаг 2.

Теперь нам нужно выяснить текущую стоимость PV пенсионного дохода Грант при \(t\) = 15. Как указывалось ранее, вычисление текущей стоимости выхода на пенсию требует двух подэтапов.

Сначала найдите текущую стоимость при \(t\) = 40, используя Формулу 11.

Потом дисконтируйте эту текущую стоимость обратно к моменту \(t\) = 15.

Найдем текущую стоимость пенсионного дохода при \(t\) = 40:

\(A\) = $100,000
\(r\) = 8% = 0.08
\(N\) = 20

\( \dst \begin{aligned}
\PV &= A \left[1- \dst {1 \over (1 + r)^N} \over r \right] \\[1ex]
&= $100,000 \left [1- \dst {1 \over (1.08)^{20} } \over 0.08 \right] \\[1ex]
&= $100,000(9.818147) = $981,814.74
\end{aligned} \)

Теперь мы должны привести полученное значение обратно к моменту \(t\) = 15:

\(\FV_N\) = $981,814.74
\(N\) = 25
\(r\) = 8% = 0.08
\( \begin{aligned}
\PV &= \FV _N (1 + r)^{-N} = $981,814.74(1.08)^{-25} \\[1ex]
&= $981,814.74(0.146018) = $143,362.53
\end{aligned} \)

Шаг 3.

Теперь напомним, что Грант накопила $54,304.23 к моменту времени \(t\) = 15.

Следовательно, приведенная стоимость сбережений за период с \(t\) = 16 до \(t\) = 40 должна равняться разнице между уже накопленной суммой ($54,304.23) и суммой, которую необходимо накопить к моменту выхода на пенсию ($143,362.53).

Эта сумма равна:

$143,362.53 - $54,304.23 = $89,058.30

Теперь мы должны рассчитать размер аннуитетного платежа A для периода с \(t\) = 16 до \(t\) = 40, текущая (приведенная) стоимость которого составляет $89,058.30.

Мы находим размер аннуитета следующим образом:

\(\PV\) = $89,058.30
\(r\) = 8% = 0.08
\(N\) = 25

\( \dst \begin{aligned}
\stRmL{Фактор приведенной}{стоимости} &=
{ \left [1- \dst {1 \over (1.08)^{25} } \over 0.08 \right]} = 10.674776
\end{aligned} \)

\( \dst \begin{aligned}
A &= \PV \Big/ \stRml{Фактор приведенной}{стоимости} \\[1ex]
&= $89,058.30/10.674776 = $8,342.87
\end{aligned} \)

Грант должна будет увеличить свои ежегодные пенсионные взносы до $8,342.87 в период с \(t\) = 16 до \(t\) = 40, чтобы достичь своей финансовой цели выхода на пенсию: увеличить пенсионные сбережения до $981,814.74 после внесения последнего пенсионного взноса в момент времени \(t\) = 40.