Как обычно измеряется доходность прямых инвестиций?

Несмотря на сложности измерения эффективности инвестиций, это должно быть сделано по причинам, упомянутым ранее - компенсации, составление бюджетов, распределение и выбор инвестиций.

Простые партнеры, полные партнеры и посредники в индустрии прямого инвестирования обычно используют два способа оценки эффективности инвестиций: собственные ставки доходности (IRR) и кратные отдачи капитала (cash-on-cash multiples).

Хотя несколько групп попыталось использовать альтернативные методы, по предпочтительному подходу нет консенсуса. Также не появилось и «отраслевого стандарта», поэтому нам необходимо понять различные методологии.

Показатель отдачи капитала

Возможно, самый простой подход - это расчет показателей отдачи капитала (cash-on-cash returns).

По сути, этот метод оценивает соотношение вернувшихся и/или в настоящий момент находящихся в фонде денег к инвестированным деньгам. Или, если быть более точными, есть один распространенный вариант - отношение распределенного капитала к оплаченному капиталу - который оценивает отношение капитала, вернувшегося к простым партнерам, к средствам, которые они предоставили.

Второй часто используемый подход - рассчитать отношение капитала, вернувшегося к простым партнерам и текущую стоимость средств фонда к средствам, которые они предоставили. По этим параметрам фонды можно сравнить с другими фондами со схожим уровнем зрелости (то есть привлеченными в тот же год).

Собственная ставка доходности

Большинство инвесторов, осуществляющих прямые инвестиции, также использует анализ первого года вливания средств, в котором собственная ставка доходности (ставка дисконтирования, при которой чистая приведенная стоимость финансовых потоков равна нулю (IRR)) отдельного фонда прямых инвестиций сравнивается с этим же показателем ряда подобных фондов, привлеченных в тот же год.

Это позволяет сделать простое сравнение, но есть множество трудностей, связанных с особенностями расчета собственной ставки доходности. (Мы рассматриваем механизм расчета собственной ставки доходности в рамке ниже.)

Механика собственной ставки доходности

Прежде чем рассматривать преимущества и недостатки IRR, давайте посмотрим на механику расчетов. Собственная ставка доходности тесно связана с подходом чистой приведенной стоимости при оценке финансовых потоков.

Чистая приведенная стоимость начинается со ставки дисконтирования - обычно, это минимальная ставка доходности, на которую согласны инвесторы. Затем определяются сроки и размеры каждого «финансового потока» - притока и оттока средств из инвестиций.

В условиях прямых инвестиций выбытие капитала из фонда рассматривается как отрицательный денежный поток; возвращение - как положительный. Рассмотрим случай, где имеют место три денежных потока (x₀, x₁ и x₂) в моменты t₀, t₁ и t₂ - соответственно. Расчет чистой приведенной стоимости этих денежных потоков в момент t₀ по ставке дисконтирования (r) можно выразить как:

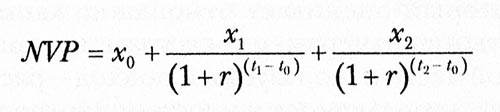
По сути, денежные потоки, которые будут иметь место в будущем, дисконтируются иди им присваивается меньший вес. Это отражает «стоимость денег во времени» - тот факт, что мы могли бы инвестировать деньги в любые другие активы в этот же период и заработать неплохую доходность.

Пока чистая приведенная стоимость, получаемая по этой формуле, является положительной, на проект стоит обратить внимание.

Расчет IRR может рассматриваться как процесс обратный этой задаче: мы рассчитываем ставку дисконтирования, при которой чистая приведенная стоимость равняется нулю. Рассмотрим предыдущий пример.

Вместо того чтобы брать заданное значение г и рассчитывать чистую приведенную стоимость (NPV), мы будем исходить из того, что NPV равна нулю. А затем мы найдем значение r, при котором обе части этого уравнения будут тождественны.

Поскольку эти расчеты так похожи, неудивительно, что они дают один и тот же ответ в простых случаях. Например, рассмотрим фонд, из которого взяли 100 долларов, а затем распределили 50 долларов наличными в конце года 1 и 150 долларов в конце года 2. Чтобы найти IRR, приравняем формулу NPV к нулю:

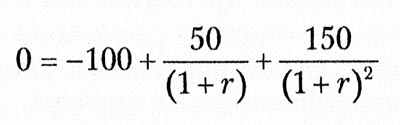
(Заметьте, что первое значение является отрицательными, поскольку денежные потоки были изъяты у инвесторов; другие значения - положительными, поскольку средства были отданы инвесторам.)

Рассмотрев различные возможные решения, находим, что уравнение будет решено при r = 0,5 или ставке дисконтирования 50%. Если бы мы захотели рассчитать NPV, мы бы вместо, этого заранее задали ставку дисконтирования r и решили бы уравнение:

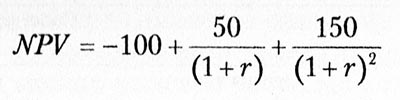
Рисунок ниже демонстрирует что обнаруживается, когда мы решаем уравнение, используя различные ставки дисконтирования.

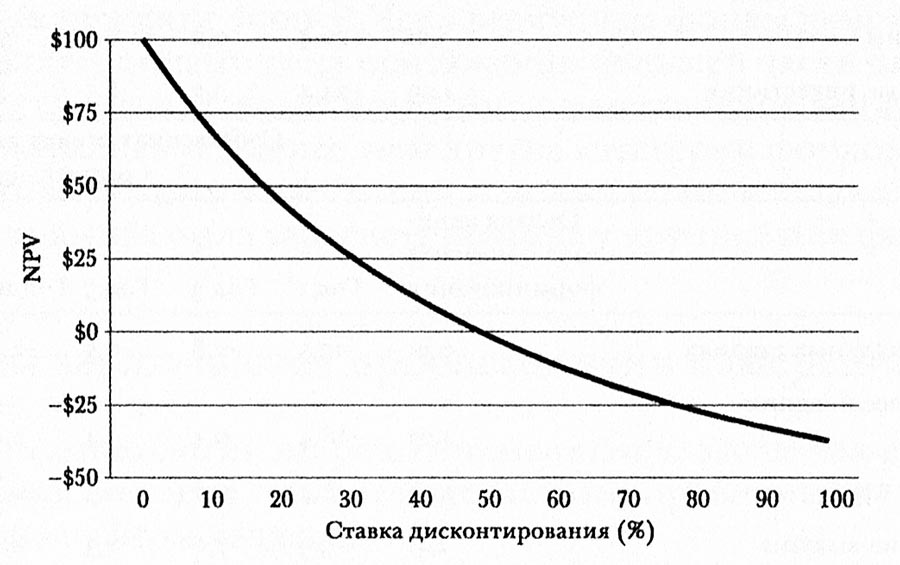Чистая приведенная стоимость изменяется обратно пропорционально ставке дисконтирования.

Пока мы используем ставку дисконтирования меньше 50% (r < 0,5), NPV является положительной. Если мы применим более высокую ставку дисконтирования, дисконтированные положительные денежные потоки не будут достаточными, чтобы покрыть первоначальные затраты, и NPV будет отрицательной.

Точка пересечения - 50% - это именно тот ответ, который мы получили при расчете IRR. В результат при оценке простых проектов или фондов с понятными денежными потоками, выбор между NPV и IRR не является значимым.

У IRR есть множество преимуществ перед кратными отдачи капитала.

Самое важное из них заключается в том, что этот метод позволяет измерить динамику серий неравномерных положительных или отрицательных денежных потоков и учитывает стоимость денег во времени.

Эти два параметра быстро стали привычными для участников отрасли прямых инвестиций, поскольку они используются так часто.

Параметры показателя отдачи капитала и
IRR для разных групп прямых инвестиций.

Примечание. Динамика в США на 31 марта 2009 г.; динамика в Европе на 31 декабря 2008 г.

Все данные по отдаче капитала представляют собой взвешенное по капиталу среднее отношение распределений и стоимости фонда к оплаченному капиталу.

Все данные по динамике IRR представляют собой объединенные аннуализированные IRR. н/д = нет данных.

В таблице выше представлена динамика фондов прямых инвестиций различных типов на различных временных отрезках, и дается средневзвешенное соотношение распределенной и остаточной стоимости фонда к оплаченному акционерному капиталу и совокупной IRR.

Эти данные взяты из базы данных Thomson Reuters по прямым инвестициям, которая является одним из стандартных источников данных по доходности и инвестициям.

Из этих таблиц можно вывести несколько закономерностей.

• Во-первых, динамика различается в зависимости от категории и региона. В частности, данные демонстрируют очень низкую эффективность европейских венчурных фондов, измеренную как по методу расчета отдачи капитала, так и по IRR.
• Во-вторых, значения IRR демонстрируют гигантский разброс по доходности в зависимости от времени. Некоторые периоды, такие как 2008 год, характеризовались очень слабой динамикой, другие, такие как конец 1990-х и середина 2000-х, были благоприятными.
• В-третьих, венчурные фонды и фонды выкупа показывали разную динамику в отдельные периоды: венчурные фонды процветали в 1990-х, а крупные фонды выкупных инвестиций - в середине 2000-х.

Хотя венчурные фонды демонстрировали вялую динамику на протяжении большей части последнего десятилетия, в конечном итоге американские венчурные фонды оказались успешнее, чем другие категории фондов.

Среди групп выкупных инвестиций в долгосрочном плане самая слабая динамика была зарегистрирована у крупнейших фондов.

Более подробное описание IRR см. здесь: CFA - Внутренняя норма доходности (IRR) и правило внутренней нормы доходности.

Другие материалы о показателе IRR.

Более подробное описание показателя NPV см. здесь: CFA - Чистая приведенная стоимость (NPV) и правило чистой приведенной стоимости.

Другие материалы о показателе NPV.