Проблемы измерения доходности прямых инвестиций

Хотя эти методологии измерения доходности широко применяются, все не так радужно. У обоих методов, увы, есть серьезные проблемы, которые мы обсудим далее.

Подход, основанный на расчете отдачи капитала, хоть и очень прост, во многих аспектах является жертвой своей простоты. Он не учитывает распределение во времени финансовых потоков, которые он сравнивает.

Это нарушает один из центральных принципов финансов, заключающийся в том, что «доллар сегодня стоит дороже, чем доллар завтра». Используя параметры отдачи капитала, мы не можем сказать, была ли доходность равномерно распределена во времени, сдвинута на начало периода или на конец периода.

Несомненно, один из вариантов может быть более предпочтителен другому, однако параметры отдачи капитала не делают различий.

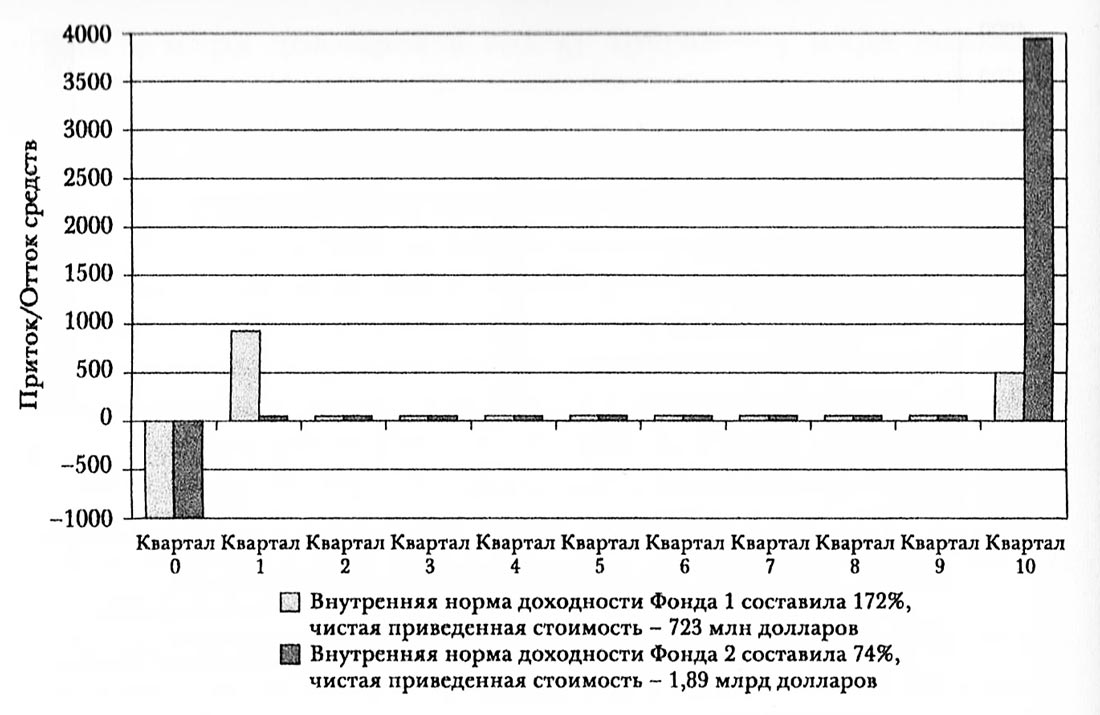
Упор на показатель отдачи капитала может привести к проблематичным решениям.

Эта проблема проиллюстрирована на рисунке выше, на котором представлены два фонда, каждый из которых привлек 1 млрд. долларов.

Первый фонд принес своим простым партнерам 3 млрд. долларов в год 5; другой - 4 млрд. долларов в год 10.

Если бы мы полагались на показатели отдачи капитала, мы бы выбрали второй фонд. Однако этот выбор не принимает во внимание, что деньги, полученные в год 5, могли быть реинвестированы, и потенциально с более высокой доходностью.

Например, если мы рассчитаем чистую приведенную стоимость, используя ставку дисконтирования 15%, первый фонд генерирует совокупную положительную доходность для инвесторов в размере почти полмиллиарда долларов. А инвесторы второго фонда фактически потеряют деньги, если судить по чистой приведенной стоимости.

Расчет чистого дохода, который не принимает во внимание стоимость денег во времени, может дать недостоверные ответы. Хотя мы можем и избежать неоправданного превознесения зайца, мы рискуем встать на защиту некоторых очень медленных черепах.

Несмотря на то, что внутренняя норма доходности лучше учитывает различия во времени, этот подход тоже не является панацеей. Здесь мы рассмотрим четыре его основных недостатка: проблему «черепахи и зайца», отсутствие систематизации; парадокс множественной IRR и проблему агрегирования.

Эзоповская аллегория «черепахи и зайца» относится к быстрому, но рассеянному зайцу, которого побеждает в соревновании медлительная, но стабильная черепаха.

Проблема черепахи и зайца

Сначала давайте рассмотрим проблему «черепахи и зайца». По сути, расчет собственной ставки доходности поощряет «зайцев» сферы прямых инвестиций - те группы прямых инвестиций, которые быстро возвращают капитал своим инвесторам.

В принципе, идея быстрого возврата денег неплоха: при прочих равных условиях, инвесторы предпочли бы получить прибыль от инвестиций скорее раньше, чем позже, поскольку тогда они смогли бы инвестировать капитал в другой фонд.

Недостаток, однако, заключается в том, что собственная ставка доходности может придавать слишком большой вес зайцам.

Практически во всех контекстах IRR отдает предпочтение тем группам, которые стараются быстро выйти из инвестиций, если конечная доходность оказывается меньше, чем у аналогов.

Это было очевидно на лихорадочном венчурном рынке конца 1990-х, когда компании в рекордное время проходили путь от стартапа до первичного размещения акций.

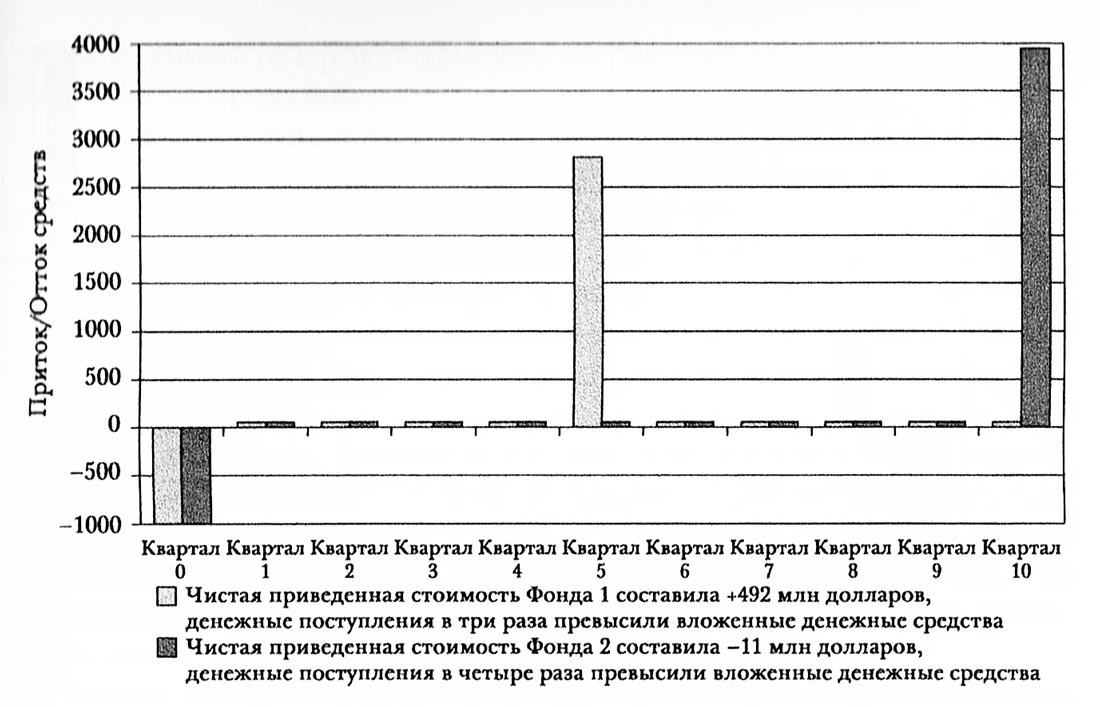
Давайте рассмотрим два фонда прямых инвестиций, в каждый из которых было инвестировано по 1 млрд. долларов. В одном случае совокупная сумма, возвращенная инвесторам, составила 2 млрд. долларов, в другом - 4 млрд. долларов.

В обоих случаях средства были возвращены сравнительно быстро, но первому фонду повезло раньше (компания была приобретена), в результате чего большая часть денег была возвращена всего через квартал. Динамика этих фондов представлена на рисунке ниже.

При расчете IRR предпочтение может быть отдано фондам с более быстрым возвратом средств перед фондами с более значительным, но более медленным возвратом средств.

Большинство инвесторов, видя, что средства в любом случае будут возвращены сравнительно быстро, предпочли бы второй фонд, поскольку прибыль на капитал в нем в три раза выше (3 млрд. долларов против 1 млрд. долларов).

Более того, если бы мы сделали анализ NPV со ставкой дисконтирования 15%, второй фонд оказался бы в лидерах (хотя коэффициент NPV составляет менее 3:1, поскольку первый фонд возвращает некоторую прибыль быстрее, чем второй фонд). Однако на расчет IRR так влияет «быстрая доходность» первого фонда, что его аннуализированная IRR более чем в два раза больше того же показателя второго фонда.

Основным фактором, который необходимо учесть, должно стать то, насколько часто у инвесторов есть возможности для инвестиций с быстрой доходностью. Если инвесторы могут рассчитывать на регулярный доступ к быстрой доходности, первый фонд может быть предпочтительным, поскольку возвращенные средства могут быть быстро реинвестированы для получения быстрой доходности в другом месте.

Эта проблема делает метод расчета отдачи капитала такой популярной альтернативой. Выбирая между группами, которые вернули средства, мы бы выбрали скорее ту группу прямых инвестиций, которая вернула больше денег, чем ту, которая сделала первое распределение.

Смотря на фактические выплаты, простые партнеры надеются избежать проблем измерения и «игры», которая иногда вредит оценкам IRR.

Отсутствие систематизации

Второй проблемой использования IRR в качестве стандартного для отрасли метода расчета эффективности является то, что в конечном итоге нет ни одного верного способа расчета IRR.

Кажется, что довольно просто следовать инструкциям в предыдущей рамке, чтобы получить аргументированные - «правильные» - результаты, однако даже небольшое изменение в применяемой методологии может привести к существенному изменению результата.

Группы прямых инвестиций очень различаются в плане их отношения к таким элементам, как сроки и оценка выхода из инвестиций, оценка компаний, остающихся в их инвестиционных портфелях, влияние налогов, и к другим деталям расчета IRR. Давайте сфокусируемся на распределении финансовых потоков во времени.

Два популярных метода расчета IRR - метод календарного времени и метод нулевого времени. Подход календарного времени (в индустрии прямых инвестиций его иногда называют взвешенным по доллару) заключается в выстраивании в ряд всех выбытий и возвратов капитала в течение года (квартала, месяца или даже дня), когда они произошли.

Если, например, в третий год существования фонда в результате IPO инвесторам вернулось 100 млн. долларов, а выбрано из фонда было 150 млн. долларов, финансовый поток за этот год будет зарегистрирован как минус 50 млн. долларов.

Если инвестиции, сделанные на третьем году жизни фонда в конечном итоге дали на восьмом году прибыль в размере 400 млн. долларов простым партнерам, этот финансовый поток будет записан, как имеющий место на восьмой год существования фонда.

Метод нулевого момента исходит из того, что все инвестиции были сделаны при открытии фонда. Так, инвестиции, осуществляемые в год 3, были бы перенесены на начальный год (год l). Подобным же образом продажа была бы перенесена на два года вперед, как если бы она случилась в год 6 (а не в год 8).

Эти различные методы, как продемонстрировано в таблице ниже, могут дать поразительно различные IRR.

Расчет IRR методом календарного времени
и методом нулевого момент.

Пример 1a: расчет методом календарного времени
	Год 0	Год 1	Год 2	Год 3	Год 4	Год 5
Инвестиции А	-100
Инвестиции В		-100				500
Всего	-100	-100	0	0	0	500
IRR	22%
Пример 1b: расчет методом нулевого момента
	Год 0	Год 1	ГОД 2	Год 3	Год 4	Год 5
Инвестиции А	-100
Инвестиции В	-100	-100			500
Всего	-200	0	0	0	500	0
IRR	26%
Пример 2а: расчет методом календарного времени
	Год 0	Год 1	Год 2	Год 3	Год 4	Год 5
Инвестиции А	-50			400
Инвестиции В		-100
Инвестиции С			-100			200
Всего	-50	-100	-100	400	0	200
IRR	43%
Пример 2b: расчет методом нулевого момента
	Год 0	Год 1	Год 2	Год 3	Год 4	Год 5
Инвестиции А	-50			400
Инвестиции В	-100
Инвестиции С	-100			200
Всего	-250	0	0	600	0	0
IRR	34%

Примечание. В каждом случае мы исходим из того, что средства были взяты у инвесторов непосредственно перед моментом инвестиций.

В Примере 1, переход от метода календарного времени к методу нулевого момента существенно повышает IRR - с 22 до 26%. В Примере 2, этот переход приводит к резкому снижению (с 43 до 34%).

Эти непредсказуемые перемены - и отсутствие стандартизованной методологии для расчета IRR - делают сравнение IRR разных групп очень проблематичным.

Проблема агрегации

Последняя проблема, которую мы выделим в этом разделе, связана с особенным способом, которым IRR объединяет информацию по многочисленным финансовым потокам. Обычно фонд прямых инвестиций вкладывает деньги в несколько сделок, а институциональный инвестор инвестирует во множество фондов.

К сожалению, способ, которым IRR отражают результаты по многочисленным фондам, никак нельзя назвать очевидным.

Эту проблему лучше проиллюстрировать на примере, чем объяснять абстрактно. Представим университетский фонд целевого капитала, который инвестирует в три фонда и хочет рассчитать ставку доходности, как показано в таблице ниже.

IRR и многочисленные фонды.

Название фонда	Размер зарезерв. капитала (млн. долл.)	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	IRR (%)
Abracadabra Ventures	100	-50	-50	0	0	0	30	0	300	20	0	22
Boring Private Equity	800	400	20	-380	50	100	150	50	75	75	0	-9
Complete Balanced Fund	500	-250	-250	0	0	100	200	250	150	300	120	14
Совокупные фин. потоки		-700	-280	-380	50	200	380	300	525	395	129
Cp. IRR												9
Средневзвеш. IRR												2
Совокупная IRR												7

Главный инвестиционный директор фонда целевого капитала рассматривает три способа сделать это:

1. Рассчитать IRR каждого фонда, а потом вывести среднее значение.
2. Рассчитать средневзвешенное значение IRR, где в качестве весов будут выступать суммы, зарезервированные для каждого фонда.
3. Суммировать все финансовые потоки, как будто они относятся к одному фонду, и сосчитать IRR финансовых потоков. Такой расчет позволяет получить так называемую совокупную IRR.

Как показывает таблица, эти три расчета дают очень разные ответы. Простое среднее значение дает самую высокую доходность, поскольку самый маленький фонд имеет самую высокую эффективность. Больше озадачивает тот факт, что совокупная

IRR дает доходность, в четыре раза превышающую средневзвешенную IRR. Если бы мы использовали другой набор показателей, результаты могли бы оказаться совсем другими. Показатель IRR может быть достаточно чувствительным к способам расчетов, и закономерности тут объяснить достаточно сложно.

Как мы видели на примере Техасского университета, отсутствие стандарта может представлять серьезные проблемы для инвесторов, осуществляющих прямые инвестиции.

В общем и целом оценка эффективности является очень важной составляющей инвестиционного решения в сфере прямого инвестирования.

Хотя решения о распределении активов, начинающиеся с оценки общего состояния экономики, имеют принципиальное значение, способность измерять эффективность и подбирать самые выгодные фонды также важна для успеха программы прямых инвестиций.

Есть ли лучший способ измерения доходности?

Учитывая ограничения расчетов отдачи капитала и собственной ставки доходности, есть ли более приемлемые способы оценки доходности прямых инвестиций? Хотя эти две методологии доминируют на практике, можно почти без сомнений ответить «да».

Перспективный подход - взглянуть на чистую приведенную стоимость фондов, нормализованную по количеству капитала, который они привлекли. Чистая приведенная стоимость, в отличие от отдачи капитала, учитывает стоимость денег во времени. Более того, она позволяет избежать многих проблем IRR.

Например, она позволяет избежать проблемы черепахи и зайца, поскольку быстрая выплата небольшого количества капитала не приведет к огромной чистой приведенной стоимости. Проблема агрегации в этом случае не возникает.

Сумма NPV двух финансовых потоков не будет отличаться от приведенной стоимости суммы финансовых потоков. Кроме того, NPV также застрахована от проблемы нескольких решений.

Основной проблемой с NPV является поиск подходящей ставки дисконтирования. Неправильно использовать очень высокие пороговые ставки доходности, употребляемые инвесторами, осуществляющими прямые инвестиции, которые объединяют и стоимость капитала, и корректировку на чрезмерный оптимизм предпринимателя.

Более целесообразным представляется использование ставки дисконтирования, которая отражает реальный ожидаемый доход организаций и лиц, которые предоставляют капитал - например, в пределах 12-18%. Этот вопрос мы рассмотрим далее.

---

Более подробное описание IRR см. здесь: CFA - Внутренняя норма доходности (IRR) и правило внутренней нормы доходности.

Другие материалы о показателе IRR.

---

Более подробное описание показателя NPV см. здесь: CFA - Чистая приведенная стоимость (NPV) и правило чистой приведенной стоимости.

Другие материалы о показателе NPV.