CFA - Обучение модели в проекте финансового прогнозирования

Метки классов настроений (положительные и отрицательные) представляют собой целевую переменную (\(y\)) для обучения модели.

Значения меток меняются на 1 (положительный класс) и 0 (отрицательный класс), чтобы можно было вычислять показатели эффективности, такие как характеристическая кривая обнаружения (ROC, receiver operating characteristic) и площадь под кривой (AUC, area under the curve) на основе результатов обученной модели.

Исходный полный набор данных, очищенный и предварительно обработанный, разделен на три отдельных поднабора данных:

Они распределены в пропорции 60:20:20 соответственно (следуя общепринятой практике). Для разделения применяется простая случайная выборка, чтобы сбалансировать распределения классов в рамках выбранной пропорции разделения.

Итоговая матрица DTM создается с использованием предложений (строки), которые являются экземплярами, а также итоговых токенов (столбцы), которые являются переменными признаков из мешка слов обучающего набора данных.

Итоговый мешок слов состоит из токенов юниграмм и биграмм из предложений, которые есть только в обучающем корпусе. Затем DTM заполняется результирующими значениями TF токенов из обучающего корпуса.

Аналогичным образом создаются матрицы DTM для CV-набора и тестового набора с использованием токенов из окончательного обучающего мешка слов для настройки, валидации и тестирования модели.

Следует прояснить, что окончательный мешок слов из обучающего корпуса используется для построения DTM для всех трех поднаборов данных (обучающий, CV и тестовый), полученных после разделения, потому что модель была обучена на этом окончательном мешке слов.

Таким образом, столбцы (признаки) всех трех DTM будут одинаковы, но количество строк варьируется из-за различного количества предложений в каждом поднаборе.

DTM заполнены итоговыми значениями частот слов, рассчитанных с использованием предложений из корпусов соответствующих поднаборов - предложений от корпуса CV-набора и предложений из корпуса тестового набора.

Иллюстрация 42 содержит итоговую сводную информацию о размерах поднаборов и их использовании в процессе обучения модели.

Как уже упоминалось, столбцы DTM поднаборов одинаковы и равны количеству уникальных токенов (то есть признаков) из окончательного мешка слов обучающего корпуса, который включает 9,188 токенов.

Обратите внимание, что это количество уникальных токенов (9,188) отличается от количества токенов в исходном корпусе (11,501), поскольку они сформировались на основе предложений, включенных в обучающий корпус с помощью случайной выборки.

Иллюстрация 42. Сводная информация о трех поднаборах данных.

Корпус	Подмножество %	Количество предложений	Размеры DTM	Цель
Исходный	100%	2180	2180 x 11501	Используется для исследования данных
Обучающий	60%	1309	1309 x 9188	Используется для обучения модели
CV	20%	435	435 x 9188	Используется для настройки и валидации обученной модели
Тестовый	20%	436	436 x 9188	Используется для тестирования обученной, настроенной и валидированной модели

Выбор метода обучения модели.

Альтернативные методы машинного обучения, включая метод SVM, деревья поиска решений и логистическую регрессию можно считать потенциально подходящими для этой конкретной задачи (то есть, контролируемого обучения), типа данных (то есть, текста) и размера данных (то есть, широкого набора данных со многими потенциальными переменными).

Метод SVM и логистическая регрессия, по-видимому, обеспечивают лучшую эффективность, чем деревья решений. Для краткости мы обсудим только логистическую регрессию.

В нашем проекте логистическая регрессия применяется для обучения модели с использованием обучающего корпуса DTM, содержащего 1,309 предложений.

Напомним, что тексты этого проекта являются предложениями, классифицированными как положительные и отрицательные классы настроений (размечены как 1 и 0, соответственно).

Токены являются переменными признаков, а класс настроений является целевой переменной.

Текстовые данные обычно содержат тысячи токенов. Это приводит к разреженным матрицам DTM, поскольку каждый столбец представляет признак токена, а значения матрицы в основном равны нулю (то есть, не все токены присутствуют в каждом тексте).

Логистическая регрессия может справляться с такими редкими обучающими данными, поскольку коэффициенты регрессии будут близки к нулю для токенов, которые отсутствуют в значительном количестве предложений.

Это позволяет модели игнорировать большое количество минимально полезных признаков. Дополнительная регуляризация помогает снизить коэффициенты в тех случаях, когда эти признаки редко встречаются и не способствуют обучению модели.

Логистическая регрессия применяется к окончательной обучающей матрице DTM для обучения модели. Поскольку этот метод использует оценку критерия максимального правдоподобия, вывод логистической модели представляет собой значение вероятности в диапазоне от 0 до 1.

Однако, поскольку целевая переменная является бинарной, коэффициенты логистической регрессии не используются напрямую для прогнозирования значения целевой переменной.

Вместо этого математическая функция использует коэффициент логистической регрессии (\(\beta\)) для расчета вероятности (\(p\)) предложений, имеющих положительное настроение (\(y = 1\)).

Если \(p\) для предложения составляет 0.90, существует вероятность 90% того, что предложение имеет положительное настроение.

Теоретически, предложения с \(p > 0.50\), вероятно, имеют положительные настроения. Однако, поскольку на практике это не всегда верно, важно найти идеальное пороговое значение \(p\). Мы уточним этот момент в последующем примере.

Пороговое значение является точкой отсечения для значений \(p\), а идеальное пороговое значение \(p\) подбирается с учетом набора данных и обучения модели.

Когда значения \(p\) (то есть вероятность предложений, имеющих положительное настроение) предложений превышают это идеальное пороговое значение \(p\), то предложения с большей вероятностью будут иметь положительное настроение (\(y = 1\)).

Идеальное пороговое значение \(p\) оценивается эвристически с использованием показателей эффективности и кривых ROC, как будет показано далее.

 

Оценка эффективности и настройка модели.

Обученная модель машинного обучения используется для прогнозирования настроений предложений из обучающих и CV матриц DTM. Иллюстрация 43 отображает кривые ROC для обучающих данных (Панель A) и CV данных (Панель B).

Помните, что ось X представляет собой ложно положительный коэффициент FP/(TN + FP), а ось Y является истинно положительным коэффициентом TP/(TP + FN).

Поскольку модель обучена с использованием обучающей матрицы DTM, она явно хорошо работает на одних и тех же обучающих данных (поэтому не нужно беспокоиться о недостаточном обучении), но не работает так же хорошо с CV данными.

Это очевидно, поскольку кривые ROC значительно отличаются для обучающих и CV данных. Показатель AUC составляет 96.5% для обучающих данных и 86.2% для CV данных.

Этот вывод свидетельствует о том, что модель работает сравнительно плохо (с более высоким уровнем ошибок или неправильной классификацией) на CV данных по сравнению с обучающими данными.

Таким образом, подразумевается, что модель переобучена.

Иллюстрация 43. Кривые ROC результатов модели для обучающих и CV данных перед регуляризацией.

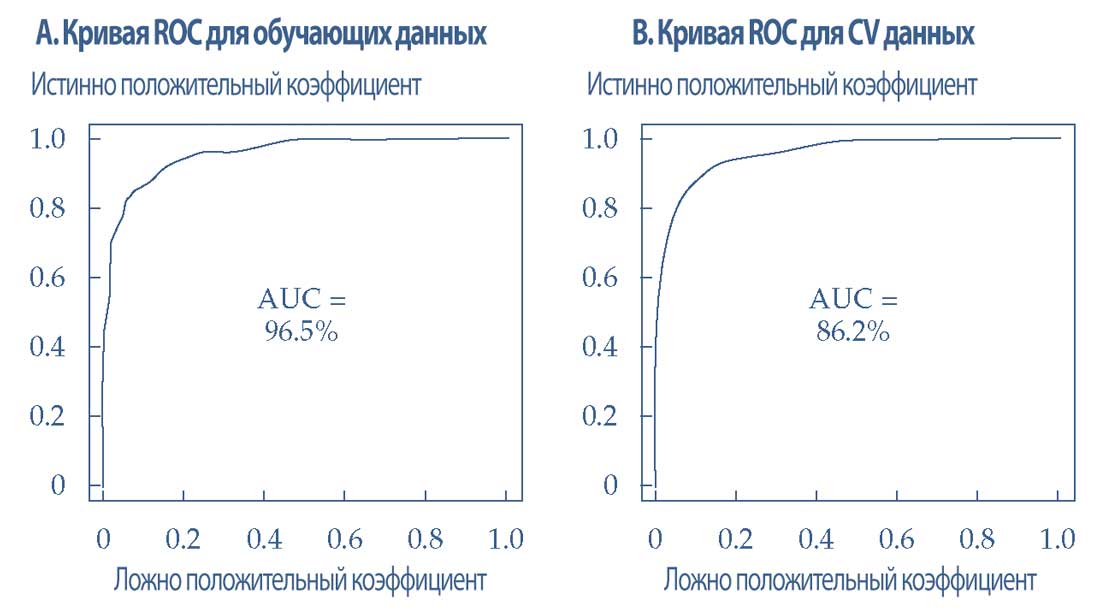
Кривые ROC результатов модели для обучающих и CV данных перед регуляризацией.

Поскольку модель переобучена, к логистической регрессии применяется регуляризация с помощью Лассо-регрессии. Лассо-регуляризация пенализирует (т.е. преуменьшает) коэффициенты логистической регрессии, чтобы предотвратить переобучение модели.

Пенализированная регрессия выбирает токены (признаки), которые имеют статистически значимые (т.е. ненулевые) коэффициенты и способствуют подгонке модели; лассо-регрессия делает это, игнорируя другие токены.

В Иллюстрации 44 показаны кривые ROC для новой модели, которая использует регулярную логистическую регрессию.

Кривые ROC показывают примерно одинаковую эффективность модели при обоих наборах данных, а AUC составляет 95.7% для обучающих данных (Панель A) и 94.8% для CV данных (Панель B).

Эти результаты показывают, что модель работает аналогичным образом как с обучающими данными, так и с CV данными и, таким образом, указывают на хорошую подгонку модели (без переобучения).

 

Иллюстрация 44. Кривые ROC результатов модели для обучающих и CV данных после регуляризации.

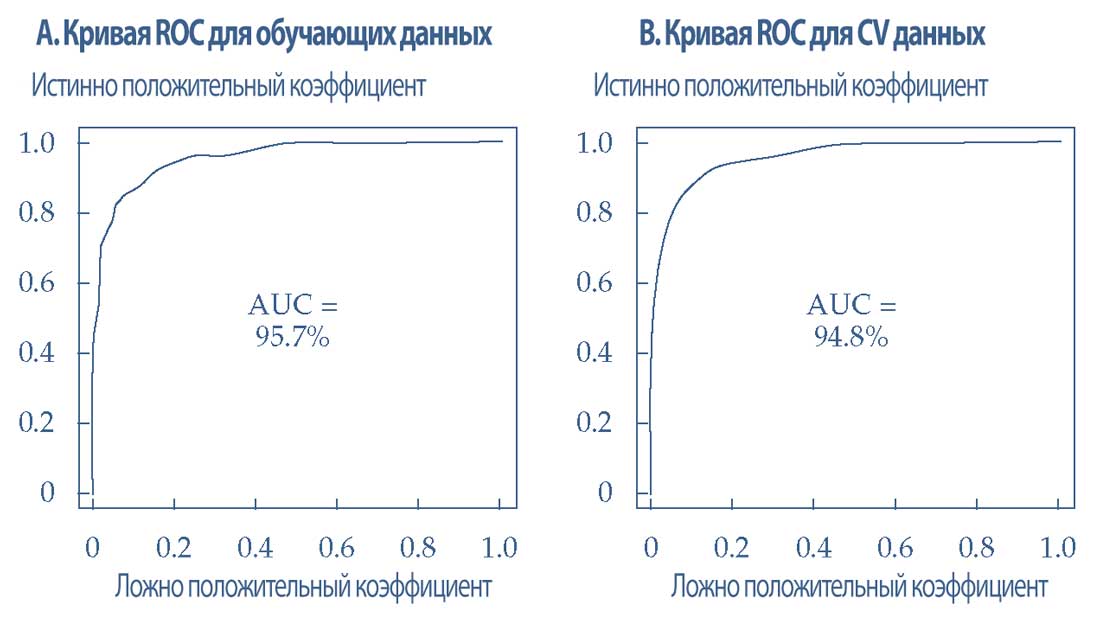
Кривые ROC результатов модели для обучающих и CV данных после регуляризации.

Регуляризация наряду с тщательным выбором признаков помогает предотвратить переобучение в моделях логистической регрессии.

Другая модель была обучена с использованием всех признаков токенов, включая стоп-слова, редкие термины и отдельные символы, без регуляризации.

Эта модель показала AUC 99.1% на обучающем наборе данных и AUC 89.4% на CV наборе данных, что позволяет предположить, что модель переобучена.

Поскольку значения AUC во всех обсуждаемых моделях близки к 100%, эти модели явно не являются недостаточно обученными.

В целом, окончательная модель для этого проекта использует логистическую регрессию с Лассо-регуляризацией.

Для дальнейшей оценки модели выполняется анализ ошибок путем вычисления матрицы неточностей с использованием результатов модели, полученных на основе CV данных.

Пороговое значение \(p = 0.5\) используется в качестве точки отсечения. Когда целевое значение \(p > 0.5\), прогноз предположительно составляет \(y = 1\) (что означает положительное настроение).

В противном случае предполагается, что прогнозом будет \(y = 1\) (отрицательное настроение).

Матрица неточностей с показателями эффективности и общими оценками результатов модели, полученных на основе CV данных, показана в Иллюстрации 45.

Иллюстрация 45. Матрица неточностей для результатов модели на основе CV данных с пороговым значением p = 0.50.

Матрица неточностей для CV данных
с пороговым значением p = 0.5.

	Фактические метки
Прогнозируемые результаты		Класс «1»	Класс «0»
	Класс «1»	284 (TP)	38 (FP)
	Класс «0»	7 (FN)	106 (TN)

Показатели эффективности.

Общая точность (accuracy) модели составляет 90% с теоретически предполагаемым (по умолчанию) пороговым значением \(p = 0.5\). Данные CV используются для настройки порогового значения, чтобы достичь наилучшей эффективности модели.

Различные значения \(p\) в диапазоне от 0.01 до 0.99 оцениваются индивидуально, а матрицы неточностей и показатели эффективности рассчитываются с использованием каждого из этих значений \(p\).

 

Основываясь на этих показателях, значение \(p\), приводящее к наилучшей общей точности модели, выбрано в качестве идеального порогового значения \(p\). Тем не менее, часто возможны компромиссы: минимизация ложно позитивных (FP) оценок достигается ценой увеличения ложно негативных (FN) оценок и наоборот.

Приоритетный выбор различных показателей эффективности (например, точность против отзывчивости) зависит от контекста проекта и относительных последствий FP и FN для проекта.

В этом проекте считается, что значимость отрицательных настроений и положительных настроений одинакова, поэтому воздействие FP и FN также равнозначно.

Обычной практикой является моделирование множества результатов при различных пороговых значениях \(p\) и поиск максимизированных значений общей точности и оценки F1, которые минимизируют эти компромиссы.

Как отмечалось ранее, общая точность и оценка F1 являются общими показателями эффективности, которые придают равный вес FP и FN.

В Иллюстрации 46 показаны общие показатели эффективности (то есть, оценка F1 и отзывчивость) для различных пороговых значений \(p\).

Теперь можно идентифицировать пороговое значение \(p\), которое приводит к наиболее высокой общей точности и оценке F1.

Из графиков в Иллюстрации 45 можно понять, что идеальное пороговое значение \(p\), по-видимому, составляет около 0.60.

Для более точного определения значения \(p\), мы генерируем таблицу показателей эффективности (то есть, точность, отзывчивость, оценка F1 и общая точность) для ряда пороговых значений \(p\) в диапазоне от 0.45 до 0.75.

Таблица в Иллюстрации 47 демонстрирует, что пороговые значения \(p\) в диапазоне от 0.60 до 0.63 приводят к наиболее высокой общей точности и оценке F1 для CV набора данных.

В результате этого анализа было выбрано итоговое значение \(p\) 0.60.

Иллюстрация 46. Пороговые значения в сравнении с общими показателями эффективности.

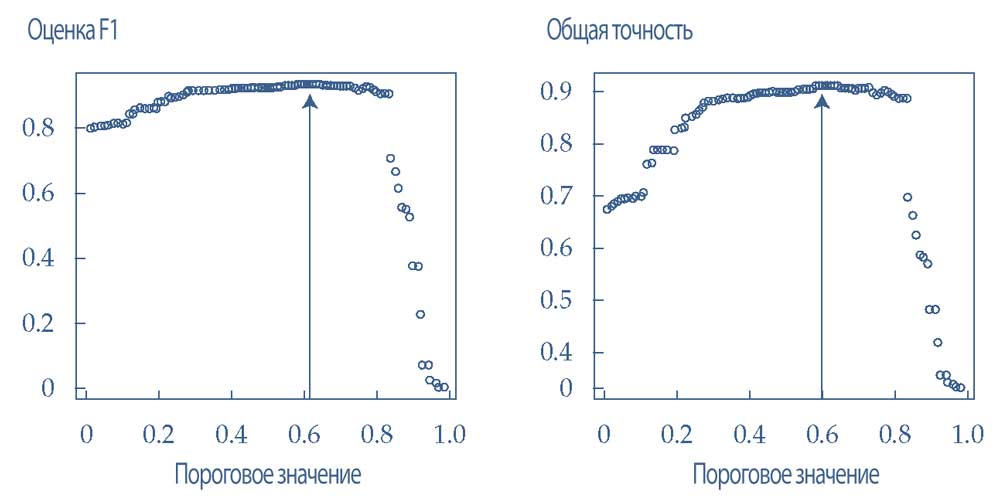
Пороговые значения в сравнении с общими показателями эффективности.

 

Иллюстрация 47. Показатели эффективности модели для ряда пороговых значений.

Порог	Точность	Отзывчивость	F1	Общая точность
0.45	0.8750000	0.986254296	0.927302100	0.8965517
0.46	0.8827160	0.982817869	0.930081301	0.9011494
0.47	0.8827160	0.982817869	0.930081301	0.9011494
0.48	0.8819876	0.975945017	0.926590538	0.8965517
0.49	0.8819876	0.975945017	0.926590538	0.8965517
0.50	0.8819876	0.975945017	0.926590538	0.8965517
0.51	0.8819876	0.975945017	0.926590538	0.8965517
0.52	0.8819876	0.975945017	0.926590538	0.8965517
0.53	0.8902821	0.975945017	0.931147541	0.9034483
0.54	0.8930818	0.975945017	0.932676519	0.9057471
0.55	0.8930818	0.975945017	0.932676519	0.9057471
0.56	0.8958991	0.975945017	0.934210526	0.9080460
0.57	0.8958991	0.975945017	0.934210526	0.9080460
0.58	0.8958991	9.975945017	0.934210526	0.9080460
0.59	0.9015873	0.975945017	0.937293729	0.9126437
0.60	0.9044586	0.975945017	0.938842975	0.9149425
0.61	0.9044586	0.975945017	0.938842975	0.9149425
0.62	0.9044586	0.975945017	0.938842975	0.9149425
0.63	0.9041534	0.972508591	0.937086093	0.9126437
0.64	0.9041534	0.972508591	0.937086093	0.9126537
0.65	0.9041534	0.972508591	0.937086093	0.9126437
0.66	0.9035370	0.965635739	0.933554817	0.9080460
0.67	0.9035370	0.965635739	0.933554817	0.9080460
0.68	0.9064516	0.965635739	0.935108153	0.9103448
0.69	0.9064516	0.965635739	0.935108153	0.9103448
0.70	0.9061489	0.962199313	0.933333333	0.9080460
0.71	0.9061489	0.962199313	0.933333333	0.9080460
0.72	0.9090909	0.962199313	0.934891486	0.9103448
0.73	0.9090909	0.962199313	0.934891486	0.9103448
0.74	0.9078947	0.948453608	0.927731092	0.9011494
0.75	0.9072848	0.941580756	0.924114671	0.8965517

Наконец, мы строим матрицу неточностей с использованием идеального порогового значения \(p\) 0.60, чтобы изучить эффективность окончательной модели.

Когда целевое значение \(p > 0.60\), предполагается, что прогноз составит \(y = 1\) (положительное настроение); в противном случае предполагается, что прогноз составит \(y = 0\) (отрицательное настроение).

Матрица неточностей для CV данных показана в Иллюстрации 48. Понятно, что показатели эффективности улучшились в окончательной модели по сравнению с первоначальной версией, когда пороговое значение \(p\) составляло 0.50.

Теперь и общая точность, и оценка F1 увеличились на один процентный пункт до 91% и 94% соответственно, в то время как точность увеличилась на два процентных пункта до 90%.

 

Иллюстрация 48. Матрица неточностей результатов модели для данных CV с пороговым значением p = 0.60.

Матрица неточностей для CV данных
с пороговым значением p = 0.6.

	Фактические метки
Прогнозируемые результаты		Класс «1»	Класс «0»
	Класс «1»	284 (TP)	30 (FP)
	Класс «0»	7 (FN)	114 (TN)

Показатели эффективности.