Во многих ситуациях, связанных с финансами и инвестициями, мы рассматриваем результат события, как успех или неудачу, или с аналогичным двоичным (бинарным) исходом, оцениваемым, как правило, как положительный и отрицательный.

Когда мы делаем вероятностные утверждения об успешных или неудачных результатах, или о чем-либо с бинарными результатами, мы часто используем биномиальное распределение (англ. 'binomial distribution').

Что представляет собой хорошая модель для изменения цены акций с течением времени?

Различные модели подходят для различных применений.

Кокс, Росс и Рубинштейн (1979) разработали модель ценообразования опционов на основе бинарных движений цены (т.е., увеличение цены или уменьшение цены), для актива, лежащего в основе опциона. Их биномиальная модель была первой из класса схожих моделей ценообразования опционов, которые сыграли важную роль в развитии индустрии производных финансовых инструментов.

Уже один этот факт был бы достаточным основанием для изучения биномиального распределения вероятностей, но биномиальное распределение также применяется в процессе принятия решений.

Случайная величина Бернулли (англ. 'Bernoulli random variable') - это базовый строительный блок биномиального распределения. Она названа в честь швейцарского математика и одного из основателей теории вероятности Якоба Бернулли (1654-1704).

Предположим, что мы проводим испытание (событие, которое может повторяться), которое приводит к одному из двух результатов. Такое испытание называют бернуллиевским испытанием (или испытанием Бернулли, англ. 'Bernoulli trial').

Если мы допустим, что Y равен 1 при успешном результате, и Y равен 0 при неудачном результате, то функция вероятности Бернулли случайной величины Y будет:

\( \begin{aligned} p(1) &= P(Y = 1) = p \\ p(0) &= P(Y = 0) = 1 - p, \end{aligned} \)

где

  • \( p \) есть вероятность того, что испытание является успешным.

Наш следующий пример - первый шаг на пути к пониманию биномиальной модели.

Пример (2) движения цены акций за 1 период в качестве случайной величины Бернулли.

Предположим, что мы описываем движение цены акций следующим образом. Цена акций сегодня равна \( S \). В следующий период цена акций может перемещаться вверх или вниз.

Вероятность движения вверх равна \( р \), а вероятность нисходящего движения равна \( 1 - р \). Таким образом, цена акции - это случайная величина Бернулли с вероятностью успеха (шаг вверх) равен р.

Когда акция движется вверх, цена закрытия (периода) составляет \( uS \), при \( u \) равной 1 плюс норма прибыли на движении вверх. Например, если акция приносит 0.01 или 1% на движении вверх, то \( u = 1.01\).

Когда акция движется вниз, цена закрытия составляет \( dS \), при d равном 1 плюс норма прибыли на движении акции вниз. Например, если акция приносит -0.01 или -1% на движении вниз, то \( d = 0.99 \).

На Рисунке 1 показана схема этой модели динамики цен на акции.

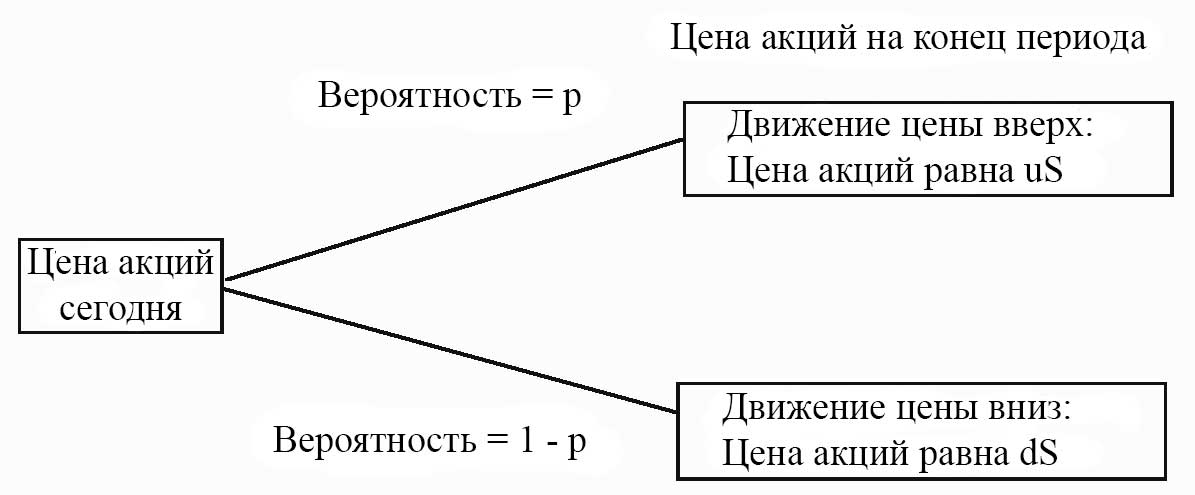Рисунок 1. Цена акций за 1 период, представленная как случайная величина Бернулли. Рисунок 1. Цена акций за 1 период, представленная как случайная величина Бернулли.

Мы продолжим разбирать вышеприведенный пример позже.

В модели движения цен на акции в Примере 2, успехи и неудачи в данном испытании связаны с движениями цены вверх и вниз, соответственно. В следующем примере, успехи являются прибыльной торговлей, а неудачи - убыточной торговлей.

Пример (3) оценки эффективности блок-брокеров (1).

Вы занимаетесь торговлей акциями для институционального фонда, который регулярно торгует с блок-брокерами.

Блоки (англ. 'blocks') - эти заявки на продажу или покупку, которые являются слишком крупными для простых участников, и обычно осуществляются в дилерских сетях или фондовых биржах.

Ваша фирма известна своим интересом к определенным видам акций.

Блок-брокеры обращаются к вам через торговую платформу, когда хотят продать пакеты акций, в покупке которых, по их мнению, ваша фирма может быть заинтересована. Вы знаете, что эти операции несут в себе определенные риски.

Например, если клиент брокера (продавец акций) имеет неблагоприятную информацию об акциях, или если вам поступила ошибочная информация об общей сумме продаж клиента брокера по всем каналам, вы можете немедленно столкнуться с убытками в торговле.

Время от времени, ваша фирма проводит аудит эффективности блок-брокеров. Ваша фирма рассчитывает пост-торговые показатели, доходность с поправкой на риск по акциям, приобретенным у блок-брокеров. На этой основе вы классифицируете каждую сделку как убыточную или прибыльную.

Вы обобщили эффективность брокеров в таблице по состоянию на 2 ноября 2014 года (имена брокеров кодируются как BB001 и BB002.)

Таблица 2. Прибыли и убытки от торговли блоками.

Ноябрь 2014

Прибыльные сделки

Убыточные сделки

BB001

3

9

BB002

5

3

Вы рассматриваете каждую сделку в качестве испытания Бернулли. Рассчитываете соотношение прибыльных сделок с двумя блочными брокерами за ноябрь 2014 г. Это оценка \( р \), лежащая в основе вероятность успешной (прибыльной) торговли с каждым брокером.

Ваша фирма произвела 3 + 9 = 12 сделок (итоговая строка) с блок-брокером BB001. Поскольку 3 из 12 сделок были успешными, процент прибыльных сделок составил 3/12 или 25%.

С брокером BB002, процент прибыльных сделок составил 5/8 или 62,5%.

Торговые сделки представляют собой испытания Бернулли, а приведенные выше расчеты дают оценки базовой вероятности прибыльной торговле (успешный исход) с двумя брокерами.

Для брокера BB001, ваша оценка равна \( \hat р = 0.25 \); для брокера BB002, ваша оценка равна \( \hat р = 0.625 \).

Математический оператор «шляпка» (hat) над \( р \) указывает на то, что это оценка \(р\), лежащая в основе вероятности прибыльной торговли с брокером.
В \( n \) испытаний Бернулли, мы можем иметь от 0 до \( n \) успехов. Если результат отдельного испытания является случайным, общее число успехов в \( n \) испытаниях также случайно.

Биномиальная случайная величина (англ. 'binomial random variable') Х определяется как число успехов в \( n \) испытаниях Бернулли. Биномиальная случайная величина представляет собой сумму случайных величин Бернулли \( Y_i, \ i = 1, 2, \ldots, \ n \):

\( \large{ X = Y_1 + Y_2 + \ldots + Y_n } \)

где

  • \( Y_i \) является результатом \(i\)-го (1, если успех; 0, если неудача).

Мы знаем, что случайная величина Бернулли определяется параметром \( р \). Число испытаний \( n \) является вторым параметром биномиальной случайной величины.

Биномиальное распределение исходит из следующих предположений:

  • Вероятность успеха \( p \) является постоянной для всех испытаний.
  • Испытания являются независимыми.

Второе предположение имеет большую упрощающую силу. Если отдельные испытания были коррелированны, вычисление вероятности заданного числа успехов в \( n \) испытаниях было бы гораздо более сложным делом.

При указанных выше двух предположениях, биномиальная случайная величина полностью описывается двумя параметрами, \( n \) и \( p \).

Мы пишем:

\( \large { X \sim B(n, p)} \)

Это выражение читается как «\( Х \) имеет биномиальное распределение с параметрами \( n \) и \( р \)».

Как вы видите, случайная величина Бернулли является биномиальной случайной величиной при \(n = 1 \): \( X \sim B(1, p) \).

Теперь мы можем найти общее выражение для вероятности того, что случайная биномиальная величина показывает \( x \) успехов в \( n \) испытаниях.

Модель динамики цен на акции можно считать обобщением любых возможных движений цен на акции, при крайне малых периодах.

Каждый период - это испытание Бернулли: с вероятностью \( p \), цена акций движется вверх; с вероятностью \( 1 - p \), цена движется вниз. Успех - это движение вверх, а \( x \) - это число движений вверх или успехов за \( n \) периодов (испытаний). При независимых испытаниях в каждого периода и постоянной величине \( p \), число движений вверх за \( n \) периодов является биномиальной случайной величиной.

Теперь мы составим выражение для \( P (X = X) \) - функцию вероятности для биномиальной случайной величины.

Любая последовательность из \( n \) периодов, которая показывает ровно \( x \) движений вверх, должна показать \( n - x \) движений вниз. У нас есть много различных способов сделать движения цены вверх и вниз, чтобы получить в общей сложности \( x \) движений вверх, но с учетом независимости испытаний, любая последовательность из \( x \) движений вверх должна произойти с вероятностью \( p^x (1 - p)^{n-x} \).

Теперь нам нужно умножить эту вероятность на количество различных способов, которыми мы можем получить последовательность их \( x \) движений. Используя базовую формулу для подсчета результатов (см. CFA - Принципы подсчета результатов в финансовом анализе), мы получим

\( \large \dst { n! \over \dst (n-x)!x! } \)

различных последовательностей в \( n \) испытаниях, которые приводят к \( x \) движениям вверх (или успехам) и \( n - x\) движениям вниз (или неудачам).

Напомним, что \( n \) факториал определяется как \( n(n-1)(n-2) \ldots 1 \) (и 0 = 1 по соглашению).

Например, \( 5! = (5)(4)(3)(2)(1) = 120 \).

Формула сочетаний (или биноминальная формула) \( n! \Big / \big[(n-x)!x! \big] \) обозначается как

\( \large \dst \binom{n}{x}  \)

(читается как «число сочетаний из n по x» или «выборка из n по x»).

Так, например, в течение трех периодов, ровно три различные последовательности имеют два движения в верх (U - up или вверх; D - down или вниз): UUD, UDU и DUU.

Мы подтверждаем это следующим образом:

\( \dst \binom{n}{x} = \frac{3!}{(3-2)!2!} = \frac{(3)(2)(1)}{(1)(2)(1)} = 3 \)

Если, гипотетически, каждая последовательность с двумя движениями вверх имела бы вероятность 0.15, то суммарная вероятность двух движений вверх за три периода будет \( 3 \times 0.15 = 0.45 \). Этот пример должен убедить вас, что для \(X\) распределенных \( B(n,p) \) вероятность \( x \) успехов в \( n \) испытаниях будет:

\( \large \dst \begin{aligned} p(x) &= P(X=x) \\ &= \binom{n}{x}p^x(1-p)^{n-x} \\ &= \frac{n!}{(n-x)!x!}p^x(1-p)^{(n-x)} \end{aligned}  \) (Формула 1)

Некоторые распределения всегда симметричны, такие, как нормальные, а другие всегда асимметричные или скошенные, такие как логнормальные (см. CFA - Симметрия и асимметрия в распределениях доходности).

Биномиальное распределение является симметричным, когда вероятность успеха на испытании составляет 0.50, в противном случае оно будет асимметричным или скошенным.

Проиллюстрируем Формулу 1 (функция вероятности) на примере симметричного распределения. Рассмотрим случайную величину, распределенную как \( B(n=5, \ p=0.50) \). Таблица 3 содержит полное описание этой случайной переменной.

Четвертая колонка Таблицы 3 равна колонке 2 (сочетания из n по x) умноженной на колонку 3, \(p^x(1-p)^{n-x} \). Колонка 4 дает вероятность для каждого числа движений вверх от колонки 1.

5 колонка представляет собой нарастающий итог 4 колонки и является кумулятивной функцией распределения (CDF, от англ. 'cumulative distribution function').

Таблица 3. Биномиальное распределение вероятностей,
при p = 0.50 и n = 5.

Количество движений вверх, x
(1)

Количество возможных способов достижения x
(2)

Вероятность для каждого способа
(3)

Вероятность для х, р(х)
(4)=(2)х(3)

F(x) = Р(Х ≤ x)
(5)

0

1

0.500(1 - 0.50)5 = 0.03125

0.03125

0.03125

1

5

0.501(1 - 0.50)4 = 0.03125

0.15625

0.18750

2

10

0.502(1 - 0.50)3 = 0.03125

0.31250

0.50000

3

10

0.503(1 - 0.50)2 = 0.03125

0.31250

0.81250

4

5

0.504(1 - 0.50)1 = 0.03125

0.15625

0.96875

5

1

0.505(1 - 0.50)0 = 0.03125

0.03125

1.00000

Что бы произошло, если бы мы сохранили параметр \(n = 5 \), но резко снизили бы вероятность успеха при испытании до 10%?

«Вероятность для каждого способа» при \(X = 0\) (нет движений вверх) тогда будет около 59%: \( 0.10^0(1 - 0.10)^5 = 0.59049 \). Поскольку нулевые успехи еще могут произойти в одном случае (колонка 2), p(0) = 59%. Вы можете проверить, что при \( p = 0.10, P(X \leq 2) = 99.14\% \): вероятность двух или менее движений вверх будет больше, чем 99%.

Вероятность случайной величины будет в основном распределяться между 0, 1 и 2 движениями вверх, а вероятность больших результатов будет мизерной.

Результаты со значением 3 и более будут длинным правым хвостом распределения, и распределение будет скошено вправо.

С другой стороны, если мы предположим, что \(p = 0.90\), мы получим зеркальное отражение распределения при \(p = 0.10\). У распределение останется перекос.

Имея под рукой объяснение биномиальной функции вероятности, мы можем продолжить разбирать наш пример блок-брокеров.

Пример (4) оценки блок-брокеров (2).

Теперь вы хотите оценить эффективность блок-брокеров из Примера 3, приведенного выше. Вы начинаете с двух вопросов:

  1. Если вы в среднем платите справедливую цену в своих сделках с брокером, какой должна быть вероятность прибыльной сделки?
  2. Будет ли каждый из брокеров соответствовать этой ожидаемой вероятности?

Вы также понимаете, что эффективность брокеров должна быть оценена в свете размера выборки, и для этого вам нужно использовать биномиальную функцию вероятности (Формула 1).

Таким образом, вы сделать следующее (со ссылкой на данные из Примера 3):

  1. Исходя из того, что цены на торгах были справедливыми,
    • A. Вычислить вероятность трех или менее прибыльных сделок с брокером BB001.
    • B. Вычислить вероятность пяти или более прибыльных сделок с брокером BB002.

Решение для частей 1 и 2:

Если цена, по которой вы торгуете, справедлива, 50% сделок с брокером должны быть прибыльными.

Конечно, вы должны скорректировать свои действия с учетом общего направления рынка и, возможно, сделать другие поправки на риск. Предположим, что эти корректировки были сделаны.

Доля прибыльных сделок с брокером BB001 составила 25%. Таким образом, брокер BB001 не соответствует ожидаемой эффективности. Брокер BB002, у которого 62.5% прибыльных сделок, наоборот, превысил ваши ожидания.

Решение для части 3:

A. Для брокера BB001, количество сделок (испытаний) было \(n = 12\) и 3 из них были прибыльны. Вам нужно вычислить вероятность трех или менее прибыльных сделок,

\( F(3) = p(3) + p(2) + p(1) + p(0) \).

Предположим, что базовая вероятность прибыльной сделки с BB001 составляет p = 0.50. При n = 12 и p = 0.50, в соответствии с формулой 1 вероятность трех прибыльных сделок будет:

\( \begin{aligned} p(3) &= \binom{n}{x}p^x(1-p)^{n-x} \\ &= \binom{12}{3}(0.50^3)(0.50^9) \\ &= \frac{12!}{(12-3)!3!} 0.50^{12} \\ &= 220(0.000244) = 0.053711 \end{aligned} \)

Вероятность ровно 3 прибыльных сделок из 12 составляет 5.4%, если брокер BB001 предоставлял вам справедливые цены. Теперь вам нужно вычислить другие вероятности:

\( \begin{aligned} p(2) &= [12!/(12 - 2)!2!](0.50^2)(0.50^{10}) = 66(0.000244) = 0.016113  \\ p(1) &= [12!/(12 - 1)!1!](0.50^1)(0.50^{11}) = 12(0.000244) = 0.00293 \\ p(0) &= [12!/(12 - 0)!0!](0.50^0)(0.50^{12}) = 1(0.000244) = 0.000244 \end{aligned} \)

Сумма всех вероятностей составляет:

F(3) = 0.053711 + 0.016113 + 0.00293 + 0.000244 = 0.072998 или 7.3%.

Вероятность сделать 3 или менее прибыльных сделок из 12 будет 7.3%, если ваша торговая платформа получала справедливые цены от брокера BB001.

B. Для брокера BB002, вы оцениваете вероятность того, что базовая вероятность прибыльной торговли с этим брокером была 50%, несмотря на хорошие результаты.

Вероятность сделать пять или более прибыльных сделок, если базовая вероятность составляет 50% будет:

1 - F(4) = p(5) + p(6) + p(7) + p(8).

Можно вычислить F(4) и вычесть его из 1, но вы также можете вычислить непосредственно p(5) + p(6) + p(7) + p(8).

Начнем с вычисления вероятности того, что именно 5 из 8 сделок были бы прибыльны, если бы BB002 предоставил вам справедливые цены:

\( \begin{aligned} p(5) &= \binom{8}{5}(0.50^5)(0.50^3) \\ &= 56(0.003906) = 0.21875 \end{aligned} \)

Вероятность составляет около 21.9%. Остальные вероятности:

\( \begin{aligned} p(6) &= 28(0.003906) = 0.109375 \\ p(7) &= 8(0.003906) = 0.03125 \\ p(8) &= 1(0.003906) = 0.003906 \end{aligned} \)

Таким образом,

p(5) + p(6) + p(7) + p(8) = 0.21875 + 0.109375 + 0.03125 + 0.003906 = 0.363281 или 36.3 процентов.

В этом примере все расчеты были осуществлены вручную, но биномиальное вероятность и функцию распределения также можно вычислить с помощью электронных таблиц.

Вероятность 36.3% является существенной; базовая вероятность справедливой торговли с BB002 вполне может быть 0.50, несмотря на ваш успех с BB002 в ноябре 2014 г. Если одну из сделок с BB002 перегруппировать из прибыльной в убыточную, то ровно половина сделок была бы прибыльной.

Таким образом, ваша торговая платформа получает справедливые цены, по крайней мере, от BB002. Вы, вероятно, захотите получить дополнительные доказательства, прежде чем заключить, что вы торгуете по более выгодным ценам, чем справедливые цены.

Величина прибыли и убытков в этих сделках является еще одним важным фактором. Если бы все прибыльные сделки приносили небольшую прибыль, но все убыточные сделки приводили к большим убыткам, то вы в итоге можете понести убытки на торгах, даже если большинство сделок будут прибыльными.

В следующем примере, биномиальное распределение поможет нам в оценке эффективности инвестиционного менеджера.

Пример (5) отслеживания ожидаемой эффективности.

Вы работаете на пенсионный фонд. Вы назначили нового менеджера портфеля в $500 млн., вложенных в индекс MSCI EAFE (Европа, Австралия и Дальний Восток), который предназначен для оценки эффективности капитала на развитых рынках, за исключением США и Канады.

После исследования, вы считаете разумным ожидать, что новый менеджер будет поддерживать доходность портфеля в пределах 75 базисных пунктов заданной доходности на ежеквартальной основе.

Вас устроит, если доходность портфеля в пределах 75 базисных пунктов будет держаться 90% времени. Менеджер достиг этой цели в 6 из 8 кварталов. Соответственно, 6 из 8 кварталов - это показатель успеха в 75%.

Но как результаты менеджера соотносятся с вашими ожиданиями уровня успеха в 90% и размером выборки в 8 наблюдений?

Для того, чтобы ответить на этот вопрос, вы должны найти вероятность того, что, с учетом предполагаемого истинного или базового показателя успеха в 90%, эффективность может быть такой же плохой, или хуже, чем предполагается. Вычислите вероятность (вручную или с помощью электронной таблицы).

В частности, вы хотите найти вероятность того, что риск портфеля находится в пределах 75 базисных пунктов в шести или менее шести из восьми кварталов.

При n = 8 и p = 0.90, эта вероятность составляет: F(6) = p(6) + p(5) + p(4) + p(3) + p(2) + p(1) + p(0).

Начните с \( p(6) = (8!/6!2!)(0.90^6)(0.10^2) = 28(0.005314) = 0.148803 \) и рассчитайте точно также другие вероятности:

\( \begin{aligned} p(5) &= (8!/5!3!)(0.90^5)(0.10^3) = 56(0.00059) = 0.033067 \\ p(4) &= (8!/4!4!)(0.90^4)(0.10^4) = 70(0.000066) = 0.004593 \\ p(3) &= (8!/3!5!)(0.90^3)(0.10^5) = 56(0.000007) = 0.000408 \\ p(2) &= (8!/2!6!)(0.90^2)(0.10^6) = 28(0.000001) = 0.000023 \\ p(1) &= (8!/1!7!)(0.90^1)(0.10^7) = 8(0.00000009) = 0.00000072 \\ p(0) &= (8!/0!8!)(0.90^0)(0.10^8) = 1(0.00000001) = 0.00000001 \end{aligned} \)

Суммируя все эти вероятности, вы заключаете, что:

F(6) = 0.148803 + 0.033067 + 0.004593 + 0.000408 + 0.000023 + 0.00000072 + 0.00000001 = 0.186895 или 18.7%.

Существует умеренная 18.7% вероятность того, что менеджер должен покажет этот результат (или худший результат), с учетом того, что он способен удовлетворить ваши ожидания в 90% времени.

Вы можете использовать другие концепции оценки, такие как отслеживание ошибок или отслеживание риска, которое определяется как стандартное отклонение доходности портфеля от его эталонной доходности для оценки эффективности менеджера. Расчет, приведенный выше, будет только одним из доводов для каких-либо выводов в отношении эффективности менеджера.

Но чтобы ответить на вопросы, связанные с вероятностью успеха, вам нужно быть квалифицированным в использовании биномиального распределения.

Две характеристики распределения, которые часто используются в инвестициях представляют собой среднее и дисперсию (или стандартное отклонение, положительный квадратный корень из дисперсии).

Среднее (или среднее арифметическое) представляет собой сумму всех значений в распределении или набора данных, деленное на количество суммированных значений.

Дисперсия является мерой разброса значений относительно среднего. См. чтения о статистических концепциях и доходности рынка для получения более подробной информации об этих понятиях.

Таблица 4 содержит выражения для среднего и дисперсии биномиальных случайных величин.

Таблица 4 Среднее и дисперсия биномиальных случайных величин.

Среднее

Дисперсия

Случайная величина Бернулли, \( B(1, p) \)

\( p \)

\( p(1 - p) \)

Биномиальная случайная величина, \( B(n, p) \)

\( np \)

\( np(1 - p) \)

Поскольку одна случайная величина Бернулли, \( Y \sim B(n, p) \), принимает значение 1 с вероятностью р и значение 0 с вероятностью 1 - р, ее среднее или средневзвешенный результата равен р. Ее дисперсия равна \( p(1-p) \).

Можно показать, что \( p(1-p) \) - это дисперсия случайной величины Бернулли следующим образом, отметив, что случайная величина Бернулли может принимать только одно из двух значений, 1 или 0:

\( \begin{aligned} \sigma ^2(Y) &= E[(Y - EY)^2] = E[(Y - p)2] \\ &= (1 - p)^2p + (0 - p)^2(1 - p) \\ &= (1 - p)[(1 - p)p + p^2] = p(1 - p) \end{aligned} \)

Общая биномиальная случайная величина, \( B(n, p) \), является суммой n случайных величин Бернулли, и таким образом, средним \( B(n, p) \) будет \(np\).

Учитывая, что величина \( B(1, p) \) имеет дисперсию \( p(1-p) \), дисперсия случайной величины \( B(n, p) \) равна произведению \( B(1, p) \) на \( n \), при условии, что все испытания (случайные величины Бернулли) являются независимыми.

Мы можем проиллюстрировать вычисления для двух биномиальных случайных величин с различными вероятностями следующим образом:

Случайная переменная

Среднее

Дисперсия

B(n = 5, p = 0.50)

2.50 = 5(0.50)

1.25 = 5(0.50)(0.50)

B(n = 5, p = 0.10)

0.50 = 5(0.10)

0.45 = 5(0.10)(0.90)

Для случайной величины B(n = 5, p = 0.50) ожидаемое число успехов составляет 2.5 со стандартным отклонением \( 1.118 = (1.25)^{1/2} \); для случайной величины B(n = 5, p = 0.10) ожидаемое число успехов составляет 0.50 со стандартным отклонением \( 0.67 = (0.45)^{1/2} \).

Пример (6) расчета ожидаемого количества дефолтов в портфеле облигаций.

Предположим, что вас, как аналитика облигаций, попросили оценить количество ожидаемых дефолтов выпущенных облигаций в течение следующего года в неуправляемом высокодоходном портфеле из 25 американских облигаций различных эмитентов.

Кредитные рейтинги облигаций в портфеле держатся в переделах рейтинга Moody's B2 / Standard & Poor B, а это означает, что облигации являются спекулятивными относительно способности выплачивать проценты и погашать основную сумму. Оценочный годовой уровень дефолта для облигаций с рейтингом B2 / B составляет 10.7%.

  1. Каким будет ожидаемое количество дефолтов в портфеле в течение следующего года, в соответствии с биномиальной моделью дефолтов?
  2. Рассчитайте стандартное отклонение количества дефолтов на ближайший год.
  3. Опишите недостатки использования биномиальной модели вероятности в данном контексте.

Решение для части 1:

Для каждой облигации, мы можем определить случайную величину Бернулли равной 1 в случае дефолта облигаций в течение года и равной 0 в противном случае. Для 25 облигаций, ожидаемое количество дефолтов в течение года составит \( np = 25(0.107) = 2.675 \) или примерно 3.

Решение для части 2:

Дисперсия будет равна:

  \( np(1 - p) = 25(0.107)(0.893) = 2.388775 \).

Стандартное отклонение:

\( (2.388775)^{1/2} = 1.55 \).

Таким образом, два стандартных отклонения образуют доверительный интервал относительно ожидаемого количества дефолтов - примерно от 0 до 6, например.

Решение для части 3:

Биномиальная модель опирается на предположение о том, что испытания независимы. Поэтому испытания связаны с тем, будет ли отдельный выпуск облигаций дефолтным в течение следующего года.

Поскольку компании-эмитенты, вероятно, подвержены общим экономическим факторам, испытания не могут быть независимыми. Тем не менее, для быстрой оценки ожидаемого количества дефолтов, биномиальная модель может быть адекватной.

Ранее мы рассмотрели простую однопериодную модель движения цены акций. Теперь мы расширили модель для описания движения цены акций за три дня подряд. Каждый день является независимым испытанием.

Акции движутся вверх с постоянной вероятностью \( p \) (вероятность перехода вверх, англ. 'up transition probability'); если они движутся вверх, \( u \) равно 1 плюс норма прибыли для движения вверх.

Акции движутся вниз с постоянной вероятностью \( 1 - p \) (вероятность перехода вниз, англ. 'down transition probability'); если они движутся вниз, \( d \) равно 1 плюс норма прибыли для движения вниз.

На Рисунке 2 изображено движение цен акций, где каждое из \( n = 3 \) движение цены акций ассоциируется с моментом времени, проиндексированным как \( t \). Форма графика демонстрирует, почему это называется биномиальным деревом (англ. 'binomial tree').

Каждое значение в прямоугольном блоке (ветви дерева), представляет собой последовательные движения или результаты и называется узлом (англ. 'node'). В этом примере узел - это потенциальное значение для котировок акций в указанный момент времени.

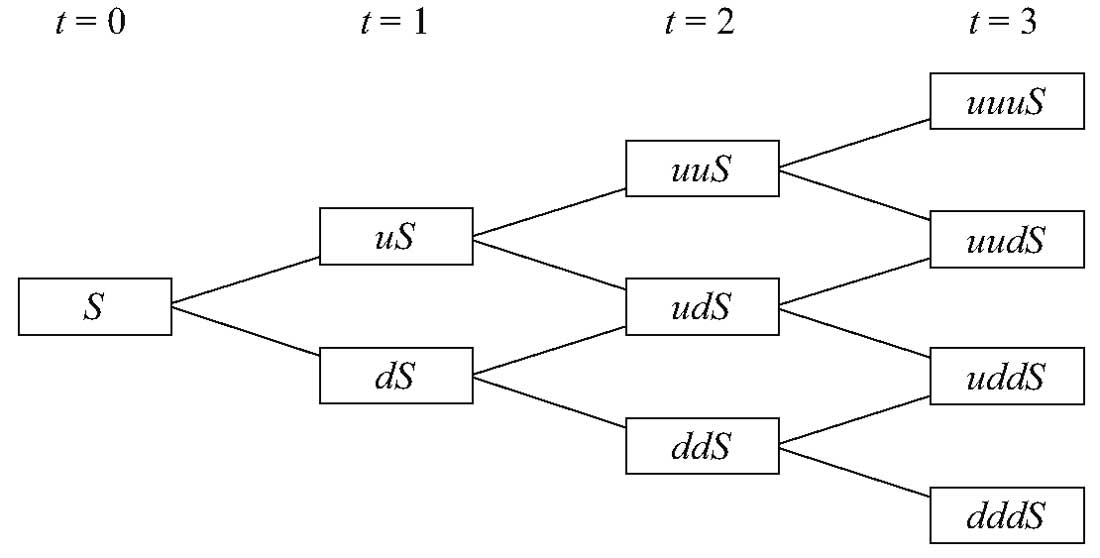Рисунок 2. Биномиальная модель движения цены акций. Рисунок 2. Биномиальная модель движения цены акций.

Мы видим из дерева, что цена акций при \( t = 3 \) имеет четыре возможных значения: \( uuuS, \ uudS, \ uddS \) и \( dddS \). Вероятность того, что цена акций равна любому из этих четырех значений задается биномиальным распределением.

Например, три последовательности движений приводят к конечной цене акции в \(uudS \): это \( uud, \ udu \), и \( duu \). Эти последовательности имеют два движения вверх из трех движений в общей сложности.

Формула сочетаний подтверждает, что число способов, чтобы получить два движения вверх (успехи) в трех периодах (испытания) составляет:

\( 3!/(3 - 2)!2! = 3 \)

Далее нужно обратить внимание, что каждая из этих последовательностей, \( uud, \ udu \), и \( duu \), имеет вероятность \( p^2(1 - p) \). Таким образом, \( P(S_3 = uudS) = 3p^2(1 - p) \), где \( S_3 \) обозначает цену акций после трех движений.

Биномиальная случайная величина здесь представляет собой количество движений вверх. Окончательное распределение цены акций зависит от начальной цены акций, количества движений вверх и размера движений вверх и вниз.

Мы не можем сказать, что цена акций сама по себе является биномиальной случайной величиной; скорее, она является функцией биномиальной случайной величины, а также \( u, \ d \) и первоначальной цены.

Этот способ моделирования цены акций полезен потому, что позволяет выбрать значения этих параметров для аппроксимации различных распределений котировок акций (с использованием большого количества периодов времени).

Например, мы можем разделить 20 дней на 100 подпериодов, позаботившись о том, чтобы использовать совместимые значения для \( u \) и \( d \).

Одно распределение, которое можно аппроксимировать, - логнормальное распределение вероятности. Оно является важной моделью непрерывного распределения цены акций, которую мы обсудим позже.

Гибкость это способа моделирования простирается далее. В дереве, показанном выше, вероятности переходов являются одинаковыми в каждом узле: \( p \) для движения вверх и \( 1 - p \) для движения вниз.

Эта стандартная формула описывает процесс, в котором волатильность доходности акций постоянна во времени. Эксперты по опционам, однако, иногда моделируют изменения волатильности во времени с использованием биномиального дерева, в котором вероятность движений вверх и вниз отличается в разных узлах.

Биномиальное дерево также обеспечивает возможность проверки условий или случайностей в любом узле. Эта гибкость полезна в инвестиционных задачах, таких как ценообразование опционов.

Рассмотрим американский колл-опцион на приносящие дивиденды ценные бумаги. (напомним, что американский опцион может быть исполнен в любое время до истечения его срока, т.е. в любом узле дерева.)

Раннее исполнение опциона может быть оптимальным, чтобы купить акции и получить дивиденды.

Денежные дивиденды представляют собой уменьшение активов компании. Раннее исполнение может быть оптимальным, поскольку цена исполнения опционов, как правило, не уменьшается на сумму денежных дивидендов, поэтому денежные дивиденды негативно влияют на положение держателя американского опциона.

Если мы моделируем стоимость акций с помощью биномиального дерева, мы можем проверить на каждом узле, является ли исполнение опциона оптимальным. Кроме того, если мы знаем стоимость покупки (колл) в четырех конечных узлах при \( t=3 \) и у нас есть модель дисконтирования стоимости на один период, мы можем сделать шаг назад на один период, до \( t=2 \), чтобы найти стоимость покупки для трех узлов в этот момент времени.

Продолжая делать шаги назад рекурсивно, мы можем найти стоимость покупки на сегодня. Этот тип рекурсивных операций легко программируется на компьютере. В результате биномиальные деревья позволяют оценивать еще более сложные опционы, чем американские колл-опционы.