Поскольку нормальное распределение вероятностей имеет так много применений, профессионалы в области финансов и инвестиций должны тщательно его изучить.

Роль нормального распределения в статистических выводах и регрессионном анализе значительно расширена благодаря центральной предельной теореме. Центральная предельная теорема (англ. 'central limit theorem') утверждает, что сумма (и среднее) большого числа независимых случайных величин приблизительно нормально распределена.

Центральная предельная теорема обсуждается далее в чтении о выборочном методе.
[см.: CFA - Центральная предельная теорема и распределение выборочного среднего]

Французский математик Абрахам Де Муавр (Abraham de Moivre, 1667-1754) ввел понятие нормального распределения в 1733 году при разработке своей версии центральной предельной теоремы.

Как показано на Рисунке 5, нормальное распределение является симметричным и имеет колоколообразную форму.

Диапазоном возможных исходов нормального распределения является вся вещественная ось: все действительные числа, лежащих между \(-\infty\) и \(+\infty\). Хвосты колоколообразной кривой распространяются без ограничений слева и справа.

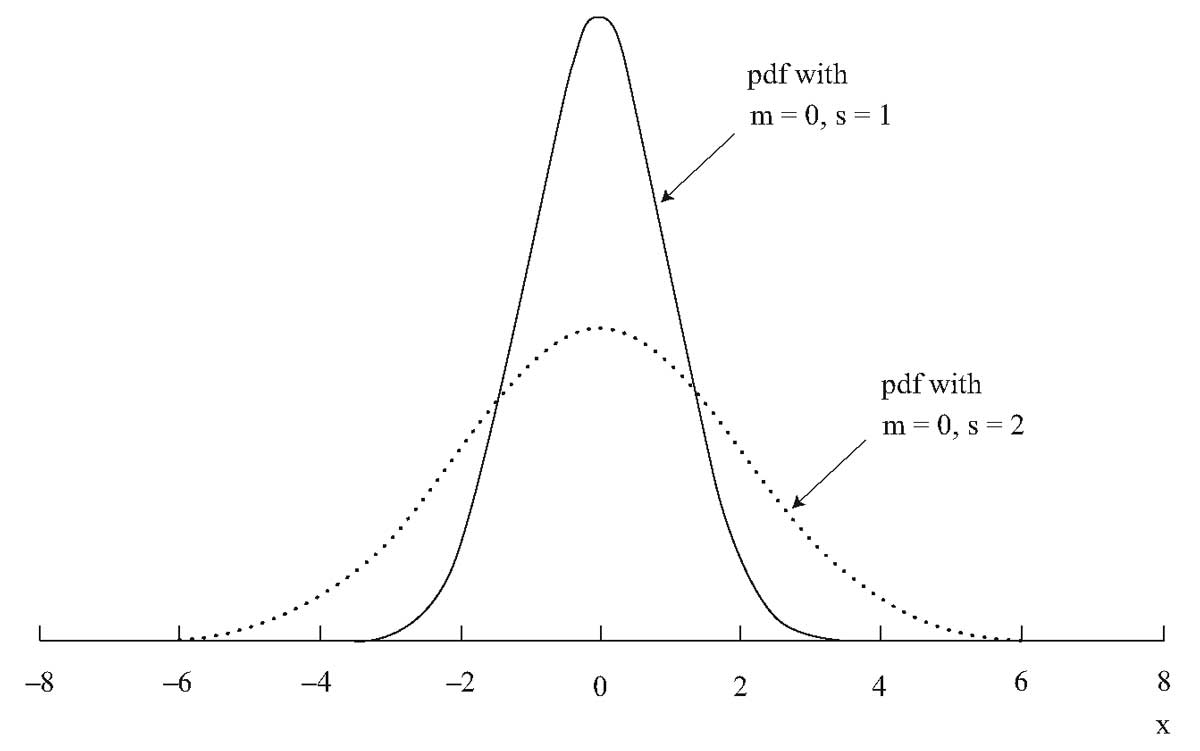Рисунок 5. Два нормальных распределения. Рисунок 5. Два нормальных распределения.

Определяющими характеристиками нормального распределения являются:

Нормальное распределение полностью описывается двумя параметрами - ее средним значением, \( \mu \), и дисперсией, \( \sigma^2 \). Обозначим это как \( X \sim N (\mu, \sigma^2) \) (читается «X имеет нормальное распределение со средним \(p\) и дисперсией \(\sigma^2\)" ).

Мы также можем определить нормальное распределение с точки зрения среднего и стандартного отклонения, \( \sigma \) (часто это удобно, так как \( \sigma \) измеряется в тех же единицах, что и \(X\) и \(\mu\)). Как следствие, мы можем ответить на любой вопрос о вероятности нормальной случайной величины, если мы знаем его среднее значение и дисперсию (или стандартное отклонение).

Нормальное распределение имеет асимметрию 0 (симметрично). Нормальное распределение имеет эксцесс (мера крутизны или островершинности распределения) 3; его избыточный эксцесс (эксцесс - 3.0) равен 0.

Если мы имеем выборку размера \(n\) из нормального распределения, мы хотим знать о возможном изменении в асимметрии и эксцессе выборки. Для нормальной случайной величины, стандартное отклонение ассиметрии выборки равно \(6/n\), стандартное отклонение эксцесса выборки равно \( 24/n \).

Как следствие симметрии, среднее, ​​медиана и мода равны для нормальной случайной величины.

Линейная комбинация двух или более нормальных случайных величин также распределена нормально.

Перечисленные характеристики касаются только одной переменной величины или одномерного нормального распределения: распределения одной нормальной случайной величины.

Одномерное распределение (англ. 'univariate distribution') описывает одну случайную величину.

Многомерное распределение (англ. 'multivariate distribution') определяет вероятности для группы связанных случайных величин. Вы столкнетесь с многомерным нормальным распределением (англ. 'multivariate normal distribution') в инвестиционной деятельности и должны знать о нем следующее.

Когда мы имеем группу финансовых активов, мы можем моделировать распределение доходности для каждого актива в отдельности, или распределение доходности для активов как для группы. «Как для группы» означает, что мы принимаем во внимание всех статистических взаимосвязей между доходностью активов.

Одна из моделей, которая часто используется для оценки доходности ценных бумаг, является многомерным нормальным распределением. Многомерное нормальное распределение для доходности ценных бумаг полностью определяется этими тремя списками параметров:

  • списком средних ставок доходности по отдельным ценным бумагам (всего \(n\) средних всего);
  • списком дисперсий доходности ценных бумаг (всего \(n\) дисперсий); а также
  • списком всех отчетливых попарных корреляций доходности (всего \(n (n - 1) / 2\) различных корреляций).

Например, распределение для двух акций (двумерное нормальное распределение) имеет 2 средние, 2 дисперсии и 1 корреляцию: \( 2 (2 - 1) / 2\).

Распределение для 30 акций имеет 30 средних, 30 дисперсий и 435 различных корреляций: \(30(30 - 1)/2 \).

Корреляция доходности акций Dow Chemical с акциями American Express такая же, как корреляция American Express с Dow Chemical, поэтому они считаются одной отчетливой корреляцией.

Необходимость в указании корреляций является отличительной чертой многомерного нормального распределения в отличии от одномерного нормального распределения.

Формулировка «предположим, что ставки доходности нормально распределены» или «предположим, что ставки доходности соответствуют нормальному распределению» иногда используется для обозначения совместного нормального распределения для нескольких ценных бумаг.

Для портфеля из 30 ценных бумаг, например, доходность портфеля представляет собой средневзвешенное значение доходности 30 ценных бумаг. Средневзвешенное значение представляет собой линейную комбинацию. Таким образом, портфель доходности нормально распределен, если доходность отдельных ценных бумаг (совместно) нормально распределена.

Напомним, что для того, чтобы указать нормальное распределение доходности портфеля, нам нужны средние значения, дисперсии, и отчетливые парные корреляции ценных бумаг портфеля.

Имея все это в виду, мы можем вернуться к нормальному распределению для одной случайной величины. Кривые на графике Рисунка 5, являются функцией плотности нормального распределения:

\( \large \dst \begin{aligned}
f(x) &= {1\over \sigma \sqrt{2\pi}} \exp{ \left( {-(x-\mu)^2 \over 2 \sigma^2} \right)} \\
& {для} -\infty < x < +\infty  \end{aligned} \) (Формула 3)

Эти две плотности, графически представленные на Рисунке 5, соответствуют среднему значению \( \mu = 0 \) и стандартным отклонениям \(\sigma = 1\) и \(\sigma = 2\). Плотность нормального распределения при  \(\mu = 0\) и \(\sigma = 1\), называется стандартным нормальным распределением (англ. 'standard normal distribution') или единичным нормальным распределением (англ. 'unit normal distribution'),

Представленные на одном графике, эти два нормальных распределения с одинаковыми средними и различными стандартными отклонениями помогают нам понять, почему стандартное отклонение является хорошей мерой дисперсии для нормального распределения:

Наблюдения гораздо больше сконцентрированы вокруг среднего значения для нормального распределения  \(\sigma = 1\), чем для нормального распределения с  \(\sigma = 2\).

Хоть это и не совсем точно, нормальное распределение можно считать приближенной моделью для ставок доходности.

Почти все вероятность нормальной случайной величины находится в пределах трех стандартных отклонений от среднего значения. Для реалистичных значений средней доходности и стандартного отклонения доходности для многих активов, нормальная вероятность результатов ниже -100% очень мала.

Полезно ли такое приближение для данного применения, является эмпирическим вопросом. Например, нормальное распределение лучше подходит для доходности за квартальные и годовые периоды владения диверсифицированным портфелем акций, чем для ежедневной или еженедельной доходности.

Постоянное отклонение от нормальности для доходности большинства долевых ценных бумаг с эксцессом больше 3 - это проблема толстых хвостов распределения. Поэтому, когда мы приближаем распределения доходности долевых инструментов с помощью нормального распределения, мы должны иметь в виду, что нормальное распределение имеет тенденцию недооценивать вероятность экстремальных значений доходности.

Толстые хвосты распределений можно смоделировать с помощью комбинации нормальных случайных величин или с помощью t-распределения Стьюдента с относительно небольшим числом степеней свободы.

Мы обсудим распределение Стьюдента далее, в чтении о выборочном методе и статистической оценке.

Доходность опционов ассиметрична. Поскольку нормальное распределение является симметричным распределением, мы должны быть осторожными в его использовании для моделирования доходности портфелей, содержащих значительные позиции по опционам.

Нормальное распределение, однако, менее подходит в качестве модели для цен на активы, чем в качестве модели для доходности активов. Нормальная случайная величина не имеет нижнего предела. Эта характеристика имеет несколько последствий для применения нормальных распределений в инвестициях. Цена актива может упасть только до 0 и в этот момент финансовый актив становится бесполезным.

В результате, на практике, финансовые аналитики, как правило, не используют нормальное распределение для моделирования распределения цен на активы. Также обратите внимание, что переход от цены актива любого уровня до 0 означает доходность -100%. Поскольку нормальное распределение распространяется ниже 0 без ограничений, оно не может быть полностью точной моделью для доходности активов.

Установив, что нормальное распределение является подходящей моделью для интересующей нас случайной величины, мы можем использовать его, чтобы сделать следующие вероятностные утверждения:

  • Приблизительно 50% всех наблюдений попадают в интервал \( \mu \pm (2/3) \sigma \).
  • Приблизительно 68% всех наблюдений попадают в интервал \( \mu \pm \sigma \).
  • Приблизительно 95% всех наблюдений попадают в интервал \( \mu \pm 2 \sigma \).
  • Приблизительно 99% всех наблюдений попадают в интервал \( \mu \pm 3 \sigma \).

Интервалы в один, два и три стандартных отклонения показаны на Рисунке 6. Эти доверительные интервалы легко запомнить, но они лишь приблизительные для указанных вероятностей. Более точные интервалы составляют \( \mu \pm 1.96\sigma \) для 95% наблюдений и \( \mu \pm 2.58\sigma \) для 99% наблюдений.

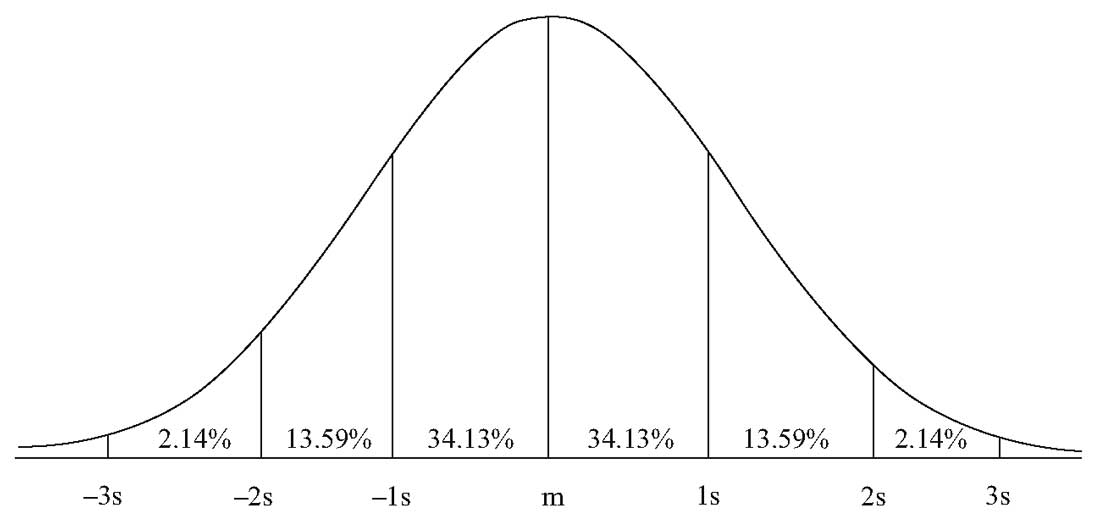Рисунок 6. Интервалы стандартного отклонения. Рисунок 6. Доверительные интервалы стандартного отклонения.

В целом, мы не наблюдаем среднее или стандартное отклонение генеральной совокупности распределения, поэтому нам нужно оценить их.

Генеральная совокупность - это все элементы указанной группы, и математическое ожидание представляет собой среднее арифметическое, рассчитанное для совокупности.

Выборка представляет собой подмножество генеральной совокупности, и выборочное среднее представляет собой среднее арифметическое для выборки.

Для получения более подробной информации об этих понятиях см. чтение о статистических концепциях и рыночной доходности.

Мы вычисляем среднее совокупности, \(\mu\), используя выборочное среднее, \( \overline X \) (иногда обозначаемое как \( \hat{\mu} \) ) и вычисляем стандартное отклонение, \(\sigma \), используя стандартное отклонение выборки, \( s \) (иногда обозначаемое как \( \hat{\sigma} \) ).

Существует столь же много различных нормальных распределений, сколько средних (\(\mu\)) и дисперсий ( \(\sigma^2 \)). Мы можем ответить на все поставленные выше вопросы с точки зрения любого нормального распределения. Электронные таблицы, например, имеют функции для расчета нормальной кумулятивной функции распределения с любыми спецификациями среднего и дисперсии.

Ради эффективности, однако, мы хотели бы свести все вероятностные утверждения к одному нормальному распределению. Стандартное нормальное распределение (нормальное распределение с \( \mu = 0 \) и \( \sigma = 1 \) ) как раз и выполняет эту роль.

Есть два шага в стандартизации случайной величины \( X \): вычесть среднее \( X \) из  \( X \), а затем разделить результат на стандартное отклонение  \( X \). Если у нас есть список наблюдений для нормальной случайной величины  \( X \), мы вычитаем среднее из каждого наблюдения, чтобы получить список отклонений от среднего значения, а затем разделить каждое отклонение на стандартное отклонение.

Результатом является стандартная нормальная случайная величина, \( Z \) (символ \(Z \) используется по соглашению в качестве символа для стандартной нормальной случайной величины).

Если мы имеем выражение \( X \sim N(\mu, \sigma^2) \) (читается «X следует нормальному распределению с параметрами \( \mu \) и \( \sigma^2 \)" ), мы стандартизируем его, используя формулу:

\( \Large \dst Z = (X-\mu)/ \sigma \) (Формула 4)

Предположим, что мы имеем нормальную случайную величину, \( X \), при \( \mu = 5 \) и \( \sigma = 1.5 \). Мы стандартизируем X с помощью выражения: \( Z = (Х - 5) /1.5 \). Например, значение \( Х = 9.5 \) соответствует стандартизованному значению 3, рассчитанному как \( Z = (9.5 - 5)/1.5 = 3 \).

Вероятность того, что мы будем наблюдать значение, не превышающее 9.5 для \( X \sim N(5,1.5) \) точно такая же, как вероятность того, что мы будем наблюдать значение, не превышающее 3 для \( Z \sim N(0.1) \).

Мы можем ответить на все вопросы о вероятности \( X \), используя стандартные значения и вероятностные таблицы для Z. Как правило, мы не знаем среднее и стандартное отклонения генеральной совокупности, поэтому мы часто используем выборочное среднее \( \overline X \) для \( \mu \) и стандартное отклонение выборки \( s \) для \( \sigma \).

Стандартные нормальные вероятности также можно вычислить с помощью электронных таблиц, статистического и эконометрического программного обеспечения и языков программирования.

В Таблице 5 приведены выдержки из таблиц кумулятивной функции распределения для стандартной нормальной случайной величины. По соглашению \( N(x) \) обозначает кумулятивную функцию распределения (cdf) для стандартной нормальной случайной величины.

Другим часто использующимся обозначением cdf стандартной нормальной случайной величины является \( \Phi (х) \).

Таблица 5. \( P(Z \leq x)=N(x) \) для \(x\geq0\)
или \( P(Z \leq z)=N(z) \) для \(z\geq0\)

x или z

0

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.00

0.5000

0.5040

0.5080

0.5120

0.5160

0.5199

0.5239

0.5279

0.5319

0.5359

0.10

0.5398

0.5438

0.5478

0.5517

0.5557

0.5596

0.5636

0.5675

0.5714

0.5753

0.20

0.5793

0.5832

0.5871

0.5910

0.5948

0.5987

0.6026

0.6064

0.6103

0.6141

0.30

0.6179

0.6217

0.6255

0.6293

0.6331

0.6368

0.6406

0.6443

0.6480

0.6517

0.40

0.6554

0.6591

0.6628

0.6664

0.6700

0.6736

0.6772

0.6808

0.6844

0.6879

0.50

0.6915

0.6950

0.6985

0.7019

0.7054

0.7088

0.7123

0.7157

0.7190

0.7224

Например, для того, чтобы найти вероятность того, что стандартная нормальная величина меньше или равна 0.24, нужно найти строку с заголовком 0.20, а также столбец с заголовком 0.04, и найти на их пересечении значение 0.5948. Таким образом, \( P(Z \leq 0.24) = 0.5948 \) или 59.48%.

Ниже приведены некоторые из наиболее часто упоминаемых значений из таблицы стандартного нормального распределения:

Точка 90-го процентиля соответствует 1.282: \( P(Z \leq 1.282) = N(1.282) = 0.90 \) или 90%, и 10% значений остаются в правом хвосте.

Точка 95-го процентиля соответствует 1.65: \( P(Z \leq 1.65) = N (1.65) = 0.95 \) или 95%, и 5% значений остаются в правом хвосте. Обратите внимание на разницу между использованием точки процентиля при работе с одним хвостом, а не двумя хвостами.

Ранее мы использовали 1.65 стандартных отклонений для 90-процентного доверительного интервала, где 5% значений лежат вне этого интервала на каждой из двух сторон. Здесь мы используем 1.65, потому что мы имеем дело с 5% значений, которые лежат только на одной стороне распределения, в правом хвосте.

Точка 99-го процентиля соответствует 2.327: \( P (Z \leq 2.327) = N(2.327) = 0.99\), или 99%, и 1% значений остается в правом хвосте.

Таблицы, которые мы даем для нормального распределения включают вероятности для \( x \leq 0 \). Многие источники, однако, дают только таблицы для \( \geq 0 \).

Как следует использовать такие таблицы, чтобы найти нормальную вероятность?

Благодаря симметрии нормального распределения, можно найти все вероятности, используя таблицы стандартной нормальной случайной величины, \( P(Z \leq x) = N(x) \) при \( х \geq 0 \).

Приведенные ниже соотношения полезны при использовании таблиц при \( х \geq 0 \), а также в других случаях:

Для неотрицательного числа \( x \), используйте \( N(x) \) из таблицы. Обратите внимание, что для вероятности справа от \( x \), мы имеем \( P(Z \geq x) = 1.0 - N(x) \).

Для отрицательного числа \( -x \), \( N(-x) = 1.0 - N(x) \): Найдите \( N(x) \) и вычтите его из 1. Вся площадь под кривой нормального распределения слева от \(x\) равна  \( N(x) \). Разница \( 1.0 - N(x) \), является площадью и вероятностью, находящейся справа от \( x \).

В силу симметрии нормального распределения вокруг его среднего значения, площадь и вероятность справа от х равна площади и вероятности слева от \( -x \), \( N(-x)\).

Для вероятности справа от \( -x \), \( P(Z \geq -x) = N(x) \).

Пример (8) расчета вероятностей для обычного портфеля акций.

Допустим, средняя доходность портфеля составляет 12%, а стандартное отклонение доходности оценивается в 22% в год.

Вы хотите вычислить следующие вероятности, при условии, что нормальное распределение описывает доходность портфеля. (Вы можете использовать приведенную выше выдержку из таблицы нормальных вероятностей, чтобы ответить на эти вопросы.)

  1. Какова вероятность того, что доходность портфеля будет превышать 20%?
  2. Какова вероятность того, что доходность портфеля будет между 12 и 20%? Другими словами, какова вероятность того, что P(12% \( \leq \) Доходность портфеля \( \leq \) 20%)?
  3. Вы можете купить годовой казначейский вексель, который приносит 5.5%. Эта доходность является эффективной годовой безрисковой процентной ставкой. Какова вероятность того, что доходность вашего портфеля не превысит безрисковую ставку?

Если \( X\) является доходностью портфеля, стандартизированной доходностью портфеля будет \( Z = (X - \overline X ) / s = (X -12\%) / 22\% \). Мы используем это выражение в решениях.

Решение для части 1:

Для \(X = 20% \), \(Z = (20 \% - 12 \%)/22 \% = 0.363636\). Вы хотите найти \(P (Z> 0.363636)\). Сначала заметим, что \( P(Z > x) = P(Z \geq x) \), так как нормальное распределение является непрерывным распределением. Напомним, что \( P(Z \geq x) = 1.0 - P(Z \leq x) \) или \( 1 - N(x) \).

Округлим 0.363636 до 0.36, в соответствии с таблицей, \( N(0.36) = 0.6406 \). Таким образом, 1 - 0.6406 = 0.3594. Вероятность того, что доходность портфеля будет превышать 20%, составляет около 36%, если ваше предположение о нормальности доходности является точным.

Решение для части 2:

P(12% \( \leq \) Доходность портфеля \( \leq \) 20%) = \( N(Z \), соответствующее \( 20 \%) - N(Z,\)  соответствующее \( 12 \% ).\)

Для первого члена выражения, \( Z = (20 \% - 12 \%) / 22 \% = 0.36 \) примерно, и \( N(0.36) = 0.6406 \( (как в решении для части 1).

Для того, чтобы сразу получить второй член выражения, обратите внимание, что 12% это среднее, и для нормального распределения 50% вероятности лежат по обе стороны от среднего значения.

Следовательно, \( N(Z,\)  соответствующее \( 12 \%)\) должно быть равно 50%. Таким образом, P(12% \( \leq \) Доходность портфеля \( \leq \) 20%) = 0.6406 - 0.50 = 0.1406 или приблизительно 14%.

Решение для части 3:

Если \( X \) является доходностью портфеля, то мы хотим найти P(Доходность портфеля - 12% \( \leq \) 5.5% - 12%). Этот вопрос является более сложным, чем в частях 1 или 2, но когда вы разберетесь в решении, представленном ниже, у вас будет полезный алгоритм для расчета вероятности других недостающих вероятностей.

Необходимо выполнить три шага, включающих стандартизацию доходности портфеля:

  • Во-первых, вычесть среднюю доходность портфеля с каждой стороны неравенства: P(Доходность портфеля - 12% \( \leq \) 5.5% - 12%).
  • Во-вторых, разделить каждую сторону неравенства на стандартное отклонение доходности портфеля: \( P[( \)Доходность портфеля \(- 12 \%)/22 \% \leq (5.5 \% - 12 \%) / 22 \%] \) \( = P(Z \leq -0.295455) = N(-0.295455) \).
  • В-третьих, признать, что на левой стороне мы имеем стандартную нормальную величину, обозначаемую как \( Z \). Как отмечалось выше, \( N(-x) = 1 - N(x) \).

Округлив -0.29545 к -0.30 для использования выдержки из таблицы, мы получим \( N(-0.30) = 1 - N(0.30) = 1 - 0.6179 = 0.3821 \) или примерно 38%. Вероятность того, что ваш портфель будет отставать от годовой безрисковой ставки составляет около 38%.

Мы можем получить тот же ответ более быстро, путем вычитания средней доходности портфеля из 5.5%, деления на стандартное отклонение доходности портфеля, и сопоставления результата (-0.295455) с вероятностной таблицей.