CFA - Свойства среднего срока погашения облигаций

Показатели дюрации Маколея и модифицированной дюрации для традиционной облигации с фиксированной ставкой являются функцией исходных переменных: купонной ставки или купонного платежа за период, доходности к погашению за период, количества оставшихся периодов до погашения и прошедшей доли текущего периода.

Свойства дюрации (среднего срока погашения) облигации получают путем изменения одной из этих переменных, оставляя неизменными другие переменные. Поскольку дюрация является основным показателем риска процентной ставки для облигации с фиксированной ставкой, эти свойства важны для понимания.

Формула в закрытой форме для дюрации Маколея, представленная ранее как Формула 4, полезна для демонстрации характеристик дюрации.

Те же характеристики используются для модифицированной дюрации.

Сначала рассмотрим прошедшую долю текущего периода ( \( t/T \) ). Показатели дюрации Маколея и модифицированной дюрации зависят от метода подсчета дней, используемого для расчета доходности к погашению.

Дюрация облигации, которая использует метод «фактические дни/фактические дни» для подсчета дней, немного отличается от дюрации аналогичной облигации, при расчете которой используется метод 30/360 дней. Ключевой момент здесь состоит в том, что при постоянной доходности к погашению (\(r\)) выражение в скобках остается неизменным в течение периода.

Следовательно, дюрация Маколея плавно уменьшается по мере того, как \(t\) меняется от \(t = 0\) до \(t = T\), что создает профиль кривой, похожий на «пилу». Этот профиль для типичной облигации с фиксированной ставкой показан в Иллюстрации 6.

Иллюстрация 6. Дюрация Маколея для разных купонных платежей с постоянной доходностью к погашению.

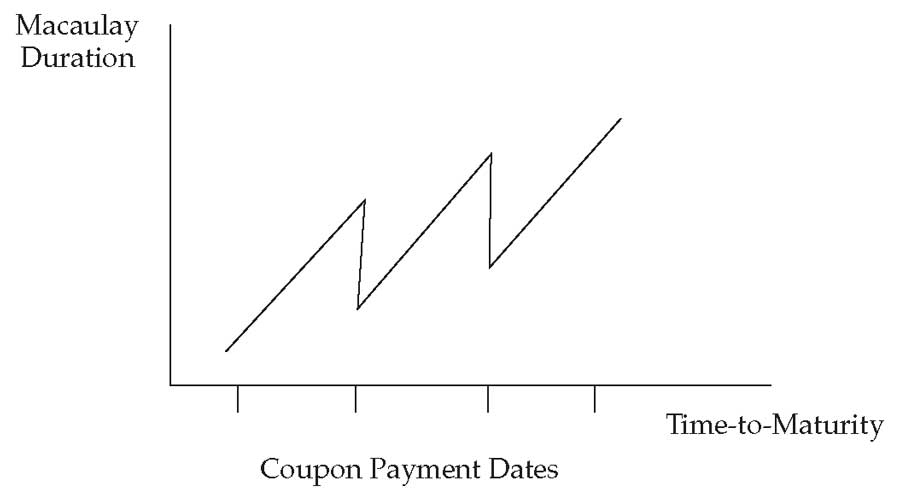
Дюрация Маколея для разных купонных платежей с постоянной доходностью к погашению.

По мере истечения периода выплаты купона (перемещение справа налево по оси X на графике), дюрация Маколея плавно снижается, а затем прыгает вверх после выплаты купона.

Свойства дюрации облигаций, связанные с изменениями в купонной ставке, доходности к погашению и оставшимся сроком погашения, показаны в Иллюстрации 7.

Иллюстрация 7. Характеристики дюрации доходности Маколея.

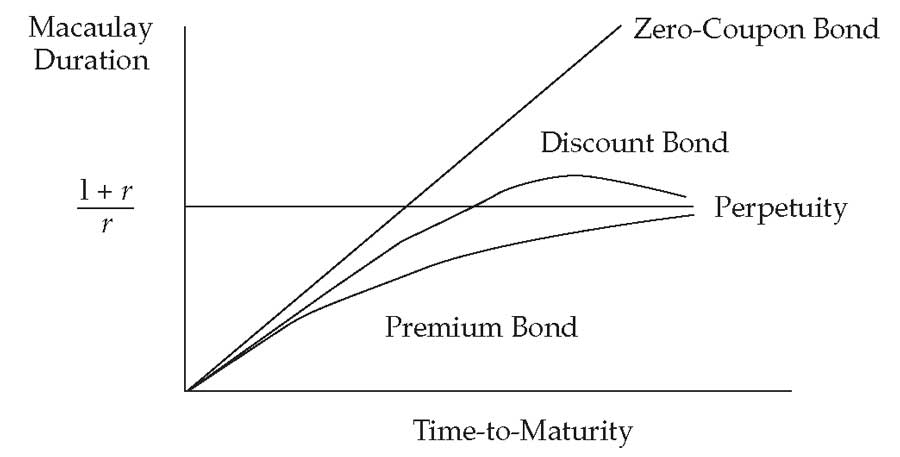
Характеристики дюрации доходности Маколея.

В Иллюстрации 7 показан график для дат купонных выплат при \(t/T = 0\) поэтому он не соответствует «пилообразному» графику, описанному выше.

Взаимосвязь между дюрацией Маколея и оставшимся сроком погашения для бескупонной облигации - это прямая под углом 45% на графике: 

MacDur = \(N\), при \(c = 0\) (и \(t/T = 0\)).

Следовательно, дюрация Маколея для бескупонной облигации - это ее оставшийся срок погашения.

Бессрочная облигация (англ. 'perpetuity' или 'perpetual bond'), которую также называют консолью ('consol'), - это облигация, которая не имеет срока погашения, т.е. погашается вечно. Она также не имеет основной суммы выкупа.

Инвестор будет получать фиксированный купон вечно, если облигация не подлежит отзыву. Безотзывные бессрочные облигации встречаются редко, но они имеют интересную дюрация Маколея: MacDur = \((1 + r)/r\), когда \(N\) стремится к бесконечности.

По сути, второе выражение внутри скобок стремится к нулю по мере увеличения количества периодов погашения, поскольку \(N\) в числителе является коэффициентом, но \(N\) в знаменателе является экспонентой, а знаменатель увеличивается быстрее, чем числитель.

Типичные купонные облигации с фиксированной ставкой с установленной датой погашения показаны в Иллюстрации 7 как премиальные и дисконтные облигации. Обычная схема заключается в том, что более длительный оставшийся срок погашения соответствует более высокому показателю дюрации Маколея.

Этот принцип всегда распространяется на облигации, торгующиеся по номинальной стоимости или с премией к номиналу. В Формуле 4 второе выражение внутри скобок является положительным числом для номинальных и премиальных облигаций.

Числитель положителен, так как ставка купона (\(c\)) больше или равна доходности к погашению (\(r\)), тогда как знаменатель всегда положителен. Следовательно, дюрация Маколея всегда меньше, чем \((1 + r)/r\), и она стремится к этому порогу снизу, по мере увеличения оставшегося срока погашения.

Любопытный результат, показанный в Иллюстрации 7, заключается в графике для дисконтных облигаций. Как правило, дюрация Маколея увеличивается в течение более длительного оставшегося срока погашения.

Но в определенный момент, когда оставшийся срок погашения оказывается достаточно высоким, дюрация Маколея превышает \( (1 + r)/r \), достигает максимума, а затем стремится к порогу сверху.

Формула 4 расширяет этот график, когда количество периодов (\(N\)) становится больше, а купонная ставка (\(c\)) становится ниже доходности к погашению (\(r\)). Затем числитель второго выражения в скобках может стать отрицательным.

Смысл этого заключается в том, что для долгосрочных дисконтных облигаций риск процентных ставок может быть меньше, чем для краткосрочных облигаций, что объясняет, почему слово «обычно» необходимо для описания взаимосвязи между ценами облигаций и их доходностью к погашению:

Обычно, при той же купонной ставке долгосрочная облигация имеет большее процентное изменение цены, чем краткосрочная облигация, когда их доходность к погашению изменяется на то же значение. Исключением является ситуация, когда долгосрочная облигация фактически имеет более низкий показатель дюрации.

Купонные ставки и ставки доходности к погашению обратно взаимосвязаны с дюрацией Маколея. В Иллюстрации 7, для одного и того же оставшегося срока погашения и доходности к погашению, дюрация Маколея будет больше для бескупонной облигации, чем для облигации с низким купоном, торгующейся с дисконтом.

Кроме того, дисконтные облигации с низким купоном имеют более высокую дюрацию, чем премиальные облигации с высоким купоном. Следовательно, при прочих равных, облигация с более низким купоном имеет более высокую дюрацию и больший риск процентной ставки, чем облигация с более высоким купоном. Этот принцип также распространяется на доходность к погашению.

Более высокая доходность к погашению снижает средневзвешенный срок получения денежных потоков. Больший вес приходится на денежные потоки, полученные в ближайшей перспективе, и меньший вес - на денежные потоки, полученные в более отдаленной перспективе, если эти денежные потоки дисконтируются по более высокой ставке.

Таким образом, дюрация Маколея и модифицированная дюрация для облигации с фиксированной ставкой зависят, главным образом, от ставки купона, доходности к погашению и оставшегося срока погашения. Более высокая ставка купона или более высокая доходность к погашению снижает показатели дюрации.

Более длительный оставшийся срок погашения обычно приводит к более высокой дюрации. Это всегда свойственно для облигации, оцениваемой с премией или по номинальной стоимости. Но если облигация оценивается с дисконтом, более длительный срок погашения может привести к снижению дюрации.

Эта ситуация возникает только в том случае, если купонная ставка низка (но не равна нулю) относительно доходности, а оставшийся срок погашения длительный.

Пример (10) расчета и анализа приблизительной модифицированной дюрации.

Хедж-фонд специализируется на инвестициях в суверенный долг страны развивающегося рынка. Менеджер фонда считает, что предполагаемая вероятность дефолта слишком высока, что означает, что облигации рассматриваются как «дешевые», а кредитные спреды слишком высокие. Хедж-фонд планирует открыть позицию по одной из этих облигаций.

Облигация	Оставшийся срок погашения	Купонная ставка	Цена	Доходность к погашению
(A)	10 лет	10%	58.075279	20%
(B)	20 лет	10%	51.304203	20%
(C)	30 лет	10%	50.210636	20%

Купон выплачивается ежегодно. Доходность к погашению соответствует эффективным годовым ставками. Цены указаны в д.е. на 100 д.е. номинальной стоимости.

1. Вычислите приблизительную модифицированную дюрацию каждой из трех облигаций, используя изменение доходности к погашению на 1 б.п., с точностью до шести знаков после запятой (поскольку показатель приблизительной дюрации очень чувствителен к округлению).
2. Какая из трех облигаций предположительно будет иметь наибольшее процентное увеличение цены, если доходность к погашению по каждой из них будет уменьшаться на одинаковое значение: например, на 10 б.п., с 20% до 19.90%?

---

Решение для части 1:

Облигация A:

Облигация B:

Облигация C:

---

Решение для части 2:

Несмотря на значительные различия в оставшихся сроках погашения (10, 20 и 30 лет), показатели приблизительной модифицированной дюрации для трех облигаций довольно схожи (4.768, 5.169 и 5.063).

Поскольку доходность к погашению настолько высока, дополнительное время для получения процентов и основных платежей по 20- и 30-летним облигациям имеет низкий вес. Тем не менее, облигация B, с 20-летним сроком, имеет самую высокую модифицированную дюрацию.

Если доходность к погашению для каждой облигации уменьшается на одинаковое значение, например, на 10 б.п., с 20% до 19.90%, облигация B, как ожидается, будет иметь наибольшее процентное увеличение цены, поскольку она имеет самую высокую модифицированную дюрацию.

Этот пример иллюстрирует взаимосвязь между дюрацией Маколея и оставшимся сроком погашения по дисконтным облигациям в Иллюстрации 7. 20-летняя облигация имеет большую дюрацию, чем 30-летняя облигация.

---

Отзывные облигации требуют использования эффективной дюрации, потому что показатели дюрации Маколея и модифицированной дюрации для них не уместны. Доходность к погашению для отзывных облигаций не очень хорошо определена, поскольку будущие денежные потоки неопределенны.

Иллюстрация 8 показывает влияние изменений в кривой базовой доходности (\(\Delta\) Curve) на цену отзывной облигации по сравнению с сопоставимой безотзывной облигацией. Эти две облигации имеют одинаковый кредитный риск, ставку купона, частоту выплат и оставшийся срок погашения.

Вертикальная ось - это цена облигации. Горизонтальная ось - это базовая доходность, например, доходность государственных облигаций.

Иллюстрация 8. Характеристики риска процентной ставки для отзывной облигации.

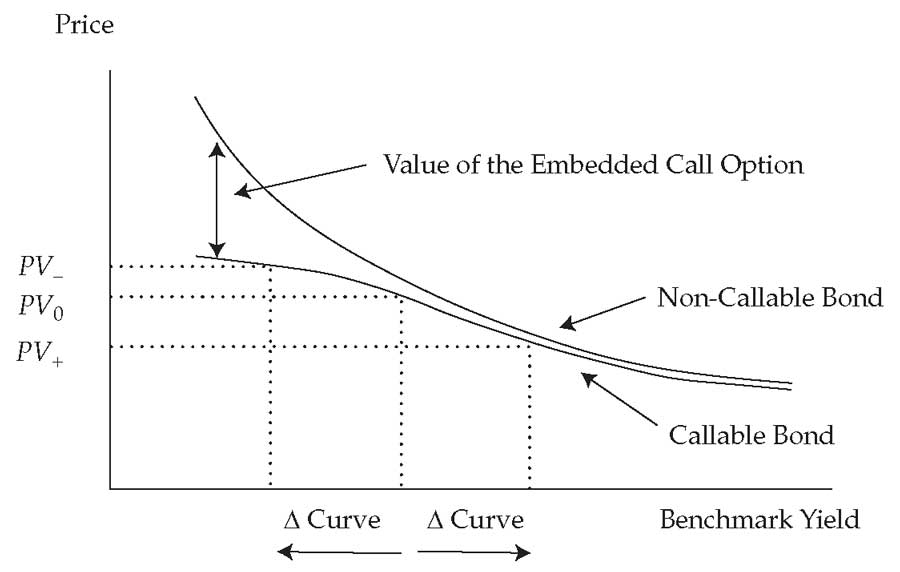
Характеристики риска процентной ставки для отзывной облигации.

Как показано в Иллюстрации 8, цена безотзывной облигации всегда больше, чем цена отзывной облигации с идентичными характеристиками. Разница определяется стоимостью встроенного опциона на отзыв (колл-опциона). Напомним, что колл-опцион является опционом (правом) для эмитента, а не для владельца облигации.

Когда процентные ставки высоки по сравнению со купонной ставкой, стоимость колл-опциона низкая. Когда ставки более низкие, стоимость колл-опциона намного больше, потому что эмитент с большей вероятностью будет использовать возможность рефинансирования долга по более низкой стоимости финансирования. Инвестор несет «риск отзыва», потому что в случае отзыва облигации инвестор должен реинвестировать поступления по более низкой процентной ставке.

Иллюстрация 8 показывает входные данные для расчета эффективной дюрации отзывной облигации. Вся кривая базовой доходности поднимается и снижается на ту же сумму, \(\Delta\) Curve. Ключевым моментом здесь является то, что когда базовая доходность высока, эффективная дюрация отзывных и безотзывных облигаций очень схожа.

Хотя иллюстрация не показывает это, наклоны линий, касающихся кривой цены, примерно одинаковы в такой ситуации. Но когда процентные ставки низки, эффективная дюрация отзывной облигации ниже, чем у сопоставимой безотзывной облигации.

Это связано с тем, что цена на облигацию не увеличивается так же сильно, когда снижается базовая доходность. Наклон линии, касающейся кривой цены, будет более плоским. Наличие колл-опциона ограничивает повышение цены.

Следовательно, встроенный колл-опцион уменьшает эффективную дюрацию облигации, особенно когда процентные ставки снижаются и облигация с большей вероятностью может быть отозвана. Более низкая эффективная дюрация также может быть интерпретирована как более короткий ожидаемый срок обращения - средневзвешенный срок получения денежного потока уменьшается.

Иллюстрация 9 рассматривает еще один встроенный опцион - пут-оцион.

Иллюстрация 9. Характеристики риска процентной ставки облигации с пут-опционом.

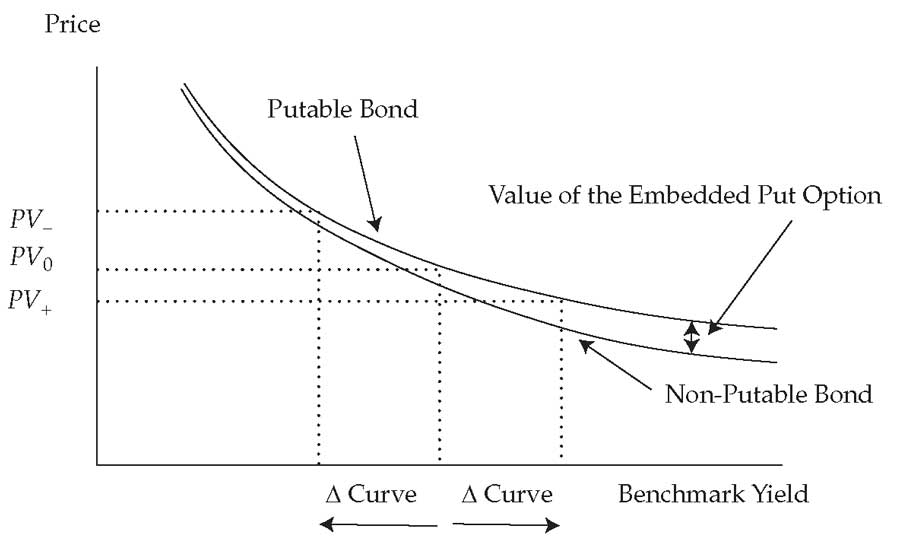
Характеристики риска процентной ставки облигации с пут-опционом.

Облигация с пут-опционом позволяет инвестору продать облигацию обратно эмитенту до наступления установленного срока погашения, обычно по номинальной стоимости, что защищает инвестора от более высокой базовой доходности или кредитных спредов, которые могли бы привести к сниженной цене.

Следовательно, цена облигации с пут-опционом всегда выше, чем у сопоставимой облигации без пут-опциона. Разница в цене - это стоимость встроенного пут-опциона.

Встроенный пут-опцион снижает эффективную дюрацию облигации, особенно когда ставки растут. Если процентные ставки низки по сравнению со ставкой купона, стоимость пут-опциона будет низкой, а влияние изменения базовой доходности на цену облигации очень похоже на влияние на цену облигации без пут-опциона.

Но когда базовые процентные ставки растут, пут-опцион становится более ценным для инвестора.

Способность продавать облигацию по номинальной стоимости ограничивает амортизацию цен по мере роста ставок. Таким образом, наличие встроенного опциона снижает чувствительность цены облигации к изменениям кривой базовой доходности, что предполагает отсутствие изменений в кредитном риске.