CFA - Средневзвешенный, модифицированный и приблизительный срок погашения облигаций
Рассмотрим средний срок погашения облигаций (дюрацию) - один из наиболее часто используемых показателей оценки риска процентных ставок по облигациям с фиксированной ставкой, - в рамках изучения ценных бумаг с фиксированным доходом по программе CFA.
Средний срок погашения облигации или дюрация (англ. 'duration') оценивает чувствительность полной цены облигации (включая начисленные проценты) к изменениям в доходности к погашению облигации или, в более общем смысле, к изменениям базовых процентных ставок.
Показатель дюрации оценивает изменения в цене облигации на основе допущения о том, что прочие переменные показатели, кроме доходности к погашению или базовых процентных ставок, будут постоянными. Наиболее важно, чтобы оставшийся срок погашения (англ. 'time-to-maturity') был неизменным.
Следовательно, средний срок погашения оценивает мгновенное (или, по крайней мере, на ту же дату) изменение цены облигации. Начисленные проценты не меняются, поэтому изменение отражает повышение или снижение фиксированной цены (англ. 'flat price') при изменении полной цены (англ. 'full price') облигации.
Средний срок погашения (дюрация) является полезным показателем, поскольку отражает приблизительное количество времени, в течение которого необходимо удерживать облигацию, чтобы реализовать рыночную ставку дисконтирования на момент покупки облигации, если возникнет единовременное изменение процентной ставки.
Если облигация удерживается в течение периода дюрации, увеличение от реинвестирования купонов компенсируется снижением цены, если процентные ставки увеличиваются, а снижение от реинвестирования купонов компенсируется увеличением цены, если процентные ставки снижаются.
Есть несколько типов дюрации облигаций. В целом, их можно разделить на дюрацию доходности и дюрацию кривой:
- Дюрация доходности (англ. 'yield duration') - это чувствительность цены облигации к доходности к погашению облигации.
- Дюрация кривой (англ. 'curve duration') - это чувствительность цены облигации (или, в более общем смысле, рыночной стоимости финансового актива или обязательства) к кривой базовой доходности.
Кривая базовой доходности (англ. 'benchmark yield curve') может быть кривой доходности государственных купонных облигаций, кривой срочных ставок (спотовой кривой) или кривой форвардных ставок, но на практике часто используется кривая доходности гособлигаций.
Показатели дюрации доходности, используемые в анализе фиксированного дохода, включают дюрацию Маколея (средневзвешенный показатель), модифицированную дюрацию, денежную дюрацию и ценовое выражение базисного пункта (PVBP).
Наиболее часто используемый показатель дюрации кривой - эффективная дюрация или эффективный средний срок погашения. Эффективная дюрация рассматривается в следующем разделе.
Дюрация Маколея или средневзвешенный срок погашения.
Дюрация Маколея, длительность Маколея или средневзвешенный срок погашения (англ. 'Macaulay duration') названа в честь Фредерика Маколея (Frederick Macaulay), канадского экономиста, который впервые описал этот показатель в своей книге, опубликованной в 1938 году.
Формула 1 является общей формулой расчета дюрации Маколея (MacDur) для традиционной облигации с фиксированной ставкой.
{(1-t/T) \times PMT \over (1+r)^{1-t/T}} +
{(2-t/T) \times PMT \over (1+r)^{2-t/T}} + \ldots +
{(N-t/T) \times (PMT+FV) \over (1+r)^{N-t/T}}
} \over { \dst
{PMT \over (1+r)^{1-t/T}} +
{PMT \over (1+r)^{2-t/T}} + \ldots +
{PMT+FV \over (1+r)^{N-t/T}}
} \right] \)
(Формула 1)
где
- \(t\) = количество дней с момента последнего купонного платежа до даты урегулирования (даты расчета).
- \(T\) = количество дней в периоде начисления купона.
- \(t/T\) = доля периода купона, которая прошла с момента последнего платежа.
- \(PMT\) = купонный платеж за период.
- \(FV\) = будущая стоимость, выплачиваемая при погашении, или номинальная стоимость облигации.
- \(r\) = доходность к погашению или рыночная ставка дисконтирования, за период.
- \(N\) = количество равномерно распределенных периодов до погашения облигации, с начала текущего периода.
Знаменатель в Формуле 1 - это полная цена (\(PV^{Full}\)) облигации, включающая начисленные проценты. Это приведенная стоимость купонных процентных и основных платежей, причем каждый денежный поток дисконтируется по одной и той же рыночной ставке, \(r\).
\( \dst
PV^{Full} = {PMT \over (1+r)^{1-t/T}} +
{PMT \over (1+r)^{2-t/T}} + \ldots +
{PMT+FV \over (1+r)^{N-t/T}} \)
(Формула 2)
Формула 3 объединяет Формулы 1 и 2, и позволяет выявить важный аспект дюрации Маколея: дюрация Маколея является средневзвешенным сроком получения обещанных платежей по облигации, где веса являются долями полной цены, соответствующими каждому обещанному будущему платежу по облигации.
\( \left\{ \begin{aligned}
&(1-t/T) \left[ { {PMT \over (1+r)^{1-t/T}} \over PV^{Full} } \right] +
(2-t/T) \left[ { {PMT \over (1+r)^{2-t/T}} \over PV^{Full} } \right] + \ldots + \\[1ex]
&(N-t/T) \left[ { {PMT+FV \over (1+r)^{N-t/T}} \over PV^{Full} } \right]
\end{aligned} \right\} \)
(Формула 3)
Число денежных поступлений, соответствующее номеру периода, составляет \(1-t/T\), \(2-t/T\), ..., \(N-t/T\). Веса являются приведенной стоимостью денежных потоков, деленной на полную цену облигации. Следовательно, дюрация Маколея оценивается с точки зрения периодов времени. Несколько примеров прояснят этот расчет.
Сначала рассмотрим 10-летнюю облигацию с 8% годовым купоном, используемую в Примерах 1-6.
Доходность к погашению облигации составляет 10.40%, а ее цена составляет 85.503075 на 100 ед. номинальной стоимости. Эта облигация имеет 10 равномерно распределенных периодов до погашения. Момент урегулирования (дата расчета) приходится на дату выплаты купона, поэтому \(t/T\) = 0.
Иллюстрация 2 показывает расчет дюрации Маколея для облигации.
Иллюстрация 2. Дюрация Маколея для 10-летней 8% облигации.
|
Период |
Денежный поток |
Приведенная стоимость |
Вес |
Период \(\times\) Вес |
|---|---|---|---|---|
|
1 |
8 |
7.246377 |
0.08475 |
0.0847 |
|
2 |
8 |
6.563747 |
0.07677 |
0.1535 |
|
3 |
8 |
5.945423 |
0.06953 |
0.2086 |
|
4 |
8 |
5.385347 |
0.06298 |
0.2519 |
|
5 |
8 |
4.878032 |
0.05705 |
0.2853 |
|
6 |
8 |
4.418507 |
0.05168 |
0.3101 |
|
7 |
8 |
4.002271 |
0.04681 |
0.3277 |
|
8 |
8 |
3.625245 |
0.04240 |
0.3392 |
|
9 |
8 |
3.283737 |
0.03840 |
0.3456 |
|
10 |
108 |
40.154389 |
0.46963 |
4.6963 |
| 85.503075 | 1.00000 | 7.0029 |
Например, окончательный платеж составляет 108 (последний купон плюс выкуп основной суммы), а его приведенная стоимость составляет 40,154389.
\( \dst {108 \over 1.1040^{10}} = 40.154389 \)
Общая сумма приведенной стоимости равна полной цене облигации.
Четвертый столбец - это вес, доля общей рыночной стоимости, соответствующая каждому денежному потоку. Окончательный платеж в размере 108 на 100 номинальной стоимости составляет 46.963% от рыночной стоимости облигации.
\( \dst {40.154389 \over 85.503075} = 0.46963 \)
Сумма весов составляет 1.00000.
Пятый столбец - это количество периодов (первый столбец), умноженное на вес (четвертый столбец). Общая сумма этого столбца составляет 7.0029, что является дюрацией Маколея или средневзвешенным сроком погашения для этой 10-летней 8% купонной облигации.
Этот показатель иногда представляют как 7.0029 лет, хотя временные рамки в большинстве случаев не требуется указывать.
Теперь рассмотрим пример, когда урегулирование (дата расчета) попадает в промежуток между датами выплаты купона.
Корпоративная облигация с полугодовым 6% купоном и погашением 14 февраля 2027 года, приобретается 11 апреля 2019 года, что соответствует дате урегулирования при расчете. Купонные платежи составляют 3 на 100 ед. номинальной стоимости и выплачиваются 14 февраля и 14 августа каждого года.
Доходность к погашению, выраженная в соответствии с «уличной конвенцией», в полугодовом исчислении, составляет 6.00%.
Полная цена этой облигации включает фиксированную цену плюс начисленные проценты. Фиксированная цена составляет 99.990423 на 100 номинальной стоимости. Начисленные проценты рассчитывается на основе соглашения 30/360 для подсчета дней.
Дата урегулирования составляет 57 дней до наступления 180-дневного полугодового периода, поэтому \(t/T = 57/180\). Начисленные проценты составляют 0.950000 (= 57/180 \(\times\) 3) на 100 номинальной стоимости.
Полная цена облигации составляет 100.940423 (= 99.990423 + 0.950000). Иллюстрация 3 показывает расчет дюрации Маколея для этой облигации.
Иллюстрация 3. Дюрация Маколея для восьмилетней облигации с полугодовым 6% купоном.
|
Период |
Срок получения |
Денежный поток |
Приведенная стоимость |
Вес |
Срок получения \(\times\) Вес |
|---|---|---|---|---|---|
|
1 |
0.6833 |
3 |
2.940012 |
0.02913 |
0.019903 |
|
2 |
1.6833 |
3 |
2.854381 |
0.02828 |
0.047601 |
|
3 |
2.6833 |
3 |
2.771244 |
0.02745 |
0.073669 |
|
4 |
3.6833 |
3 |
2.690528 |
0.02665 |
0.098178 |
|
5 |
4.6833 |
3 |
2.612163 |
0.02588 |
0.121197 |
|
6 |
5.6833 |
3 |
2.536080 |
0.02512 |
0.142791 |
|
7 |
6.6833 |
3 |
2.462214 |
0.02439 |
0.163025 |
|
8 |
7.6833 |
3 |
2.390499 |
0.02368 |
0.181959 |
|
9 |
8.6833 |
3 |
2.320873 |
0.02299 |
0.199652 |
|
10 |
9.6833 |
3 |
2.253275 |
0.02232 |
0.216159 |
|
11 |
10.6833 |
3 |
2.187645 |
0.02167 |
0.231536 |
|
12 |
11.6833 |
3 |
2.123927 |
0.02104 |
0.245834 |
|
13 |
12.6833 |
3 |
2.062065 |
0.02043 |
0.259102 |
|
14 |
13.6833 |
3 |
2.002005 |
0.01983 |
0.271389 |
|
15 |
14.6833 |
3 |
1.943694 |
0.01926 |
0.282740 |
|
16 |
15.6833 |
103 |
64.789817 |
0.64186 |
10.066535 |
|
100.940423 |
1.00000 |
12.621268 |
Расчет включает 16 полугодовых периодов с даты выплаты последнего купона 14 февраля 2019 года до даты погашения 14 февраля 2027 года. Срок получения денежного потока в полугодовые периоды приведен во втором столбце: 0.6833 = 1 - 57/180, 1.6833 = 2 - 57/180 и т.д.
Денежный поток для каждого периода приведен в третьем столбце. Годовая доходность к погашению составляет 6.00%, поэтому доходность за полугодовой период составляет 3.00%. Эта доходность используется для расчета приведенной стоимости каждого денежного потока в четвертом столбце, а его общая сумма соответствует полной цене облигации и равна 100.940423.
Веса, которые являются долями полной цены, соответствующими каждому денежному потоку, приведены в пятом столбце.
Дюрация Маколея - это сумма значений в шестом столбце, которые рассчитываются умножением срока получения на вес каждого денежного потока. Полученный результат, 12.621268, является показателем дюрации Маколея по восьмилетней 6% облигации при расчете на 11 апреля 2019 года, выраженным в полугодовом исчислении.
Подобно купонным ставками и ставкам доходности, показатель дюрации на практике всегда рассчитывается в годовом исчислении.
Следовательно, дюрация Маколей обычно представляется как 6.310634 года (= 12.621268/2). Такая высокая точность не требуется на практике. Как правило, «6,31 года» достаточно. Полная точность здесь показана для иллюстрации расчетов.
Пользователи Microsoft Excel могут рассчитать дюрацию Маколея, используя финансовую функцию DURATION / ДЛИТЕЛЬНОСТЬ.
Другим подходом к расчету дюрации Маколея является использование общей формулы для облигации с фиксированной ставкой (Формула 4), где \(c\) - ставка купона за период (PMT/FV).
Пошаговое получение этой формулы приведено в книге Donald J. Smith, Bond Math: The Theory behind the Formulas, 2nd edition (Hoboken, NJ: John Wiley & Sons, 2014).
MacDur =
\( \dst \left\{ {1+r \over r} -
{ 1+r+ \big[N \times (c-r) \big] \over
c \times \big[ (1+r)^N -1 \big] +r }
\right\} - t/T \)
(Формула 4)
Дюрация Маколея для 10-летней облигации с годовым 8% купоном рассчитывается путем применения параметров \(r\) = 0.1040, \(с\) = 0.0800, \(N\) = 10 и \(t/T\) = 0 к Формуле 4.
\( \dst {1+0.1040 \over 0.1040} -
{1+0.1040 + [10 \times (0.0800-0.1040)]
\over 0.0800 \times \big[ (1+0.1040)^{10} - 1 \big] + 0.1040 }
\) = 7.0029
Таким образом, средневзвешенный срок получения процентов и основных платежей, который приведет к реализации первоначальной рыночной ставки дисконтирования этой 10-летней облигации, составляет 7.00 лет.
Дюрация Маколея для облигации с полугодовым 6% купоном и погашением 14 февраля 2027 года рассчитывается путем применения параметров \(r\) = 0.0300, \(с\) = 0.0300, \(N\) = 16 и \(t/T\) = 57/180 к Формуле 4.
\( \dst {1+0.0300 \over 0.0300} -
{1+0.0300 + [16 \times (0.0300-0.0300)]
\over 0.0300 \times \big[ (1+0.0300)^{16} - 1 \big] + 0.0300 } - (57/180)
\) = 12.621268
Формула 4 использует доходность к погашению за период, ставку купона за период, количество периодов до погашения и прошедшую долю текущего периода. Формула рассчитывает дюрацию Маколея, выраженную в периодах. Ее можно преобразовать в годовое исчисление путем деления на количество периодов в году.
Модифицированная дюрация.
Расчет показателя модифицированного средневзвешенного срока погашения или модифицированной дюрации (modified duration, ModDur) для облигации требует простой корректировки дюрации Маколея. Это показатель дюрации Маколея, разделенный на один плюс доходность за период.
\( \dst {\rm ModDur} = { {\rm MacDur} \over 1+r } \)
(Формула 5)
Например, модифицированная дюрация для 10-летней облигации с 8% годовым купоном составляет 6.3432.
\( \dst {\rm ModDur} = { 7.0029 \over 1.1040 } = 6.3432 \)
Модифицированная дюрация по облигации с 6% полугодовым купоном и погашением 14 февраля 2027 года составляет 12.253658 полугодовых периодов.
\( \dst {\rm ModDur} = { 12.621268 \over 1.0300 } = 12.253658 \)
Годовая модифицированная дюрация этой облигации составляет 6.126829 (= 12.253658/2).
Хотя модифицированная дюрация может показаться лишь дюрацией Маколея с незначительной корректировкой, она имеет важное применение в оценке риска: модифицированная дюрация обеспечивает оценку процентного изменения цены для облигации, с учетом изменение ее доходности к погашению.
\( \%\Delta PV^{Full} \approx -{\rm AnnModDur} \times \Delta {\rm Yield} \)
(Формула 6)
Процентное изменение цены относится к полной цене, включая начисленные проценты. AnnModDur в Формуле 6 - это годовая модифицированная дюрация, а \(\Delta {\rm Yield}\) - это изменение годовой доходности к погашению.
Знак \(\approx \) указывает на то, что этот расчет является оценочным. Знак минуса указывает на то, что цена облигации и доходность к погашению обратно пропорциональны.
Если годовая доходность облигации с 6% полугодовым купоном, которая погашается 14 февраля 2027 года, увеличивается на 100 б.п., с 6.00% до 7.00%, предполагаемый убыток стоимости облигации составляет 6.1268%.
\( \%\Delta PV^{Full} \approx -6.126829 \times 0.0100 = -0.061268 \)
Если доходность к погашению должна была снизиться на 100 б.п. до 5.00%, предполагаемый прирост стоимости составил бы 6.1268%.
\( \%\Delta PV^{Full} \approx -6.126829 \times -0.0100 = 0.061268 \)
Модифицированная дюрация обеспечивает линейную оценку процентного изменения цены. В абсолютном выражении, изменение будет одинаково либо при увеличении, либо при уменьшении доходности к погашению.
Напомним (см. чтение «Введение в оценку фиксированного дохода»), что для данной ставки купона и оставшегося срока погашения процентное изменение цены (в абсолютном выражении) будет больше, когда ставка рыночная ставка дисконтирования снижается, чем когда она увеличивается.
Позже в этом чтении вводится термин «поправка на выпуклость» для дюрации. Она повышает точность этой оценки, особенно когда рассматривается большое изменение доходности к погашению (например, 100 б.п.).
Приблизительная оценка модифицированной дюрации.
Модифицированный показатель дюрации для облигации с фиксированной ставкой можно легко получить, если уже известна дюрация Маколея. Альтернативный подход заключается в приблизительной оценке напрямую. Формула 7 позволяет приблизительно рассчитать годовую модифицированную дюрацию.
\( \dst {\rm ApproxModDur} = { (PV_-) - (PV_+) \over
2 \times (\Delta {\rm Yield}) \times (PV_0) } \)
(Формула 7)
Цель приближения (аппроксимации) состоит в том, чтобы оценить наклон линии, касающейся кривой цены-доходности. Касательная линия, кривая и область приближения кривой показаны в Иллюстрации 4.
Иллюстрации 4. Приблизительная модифицированная дюрация.
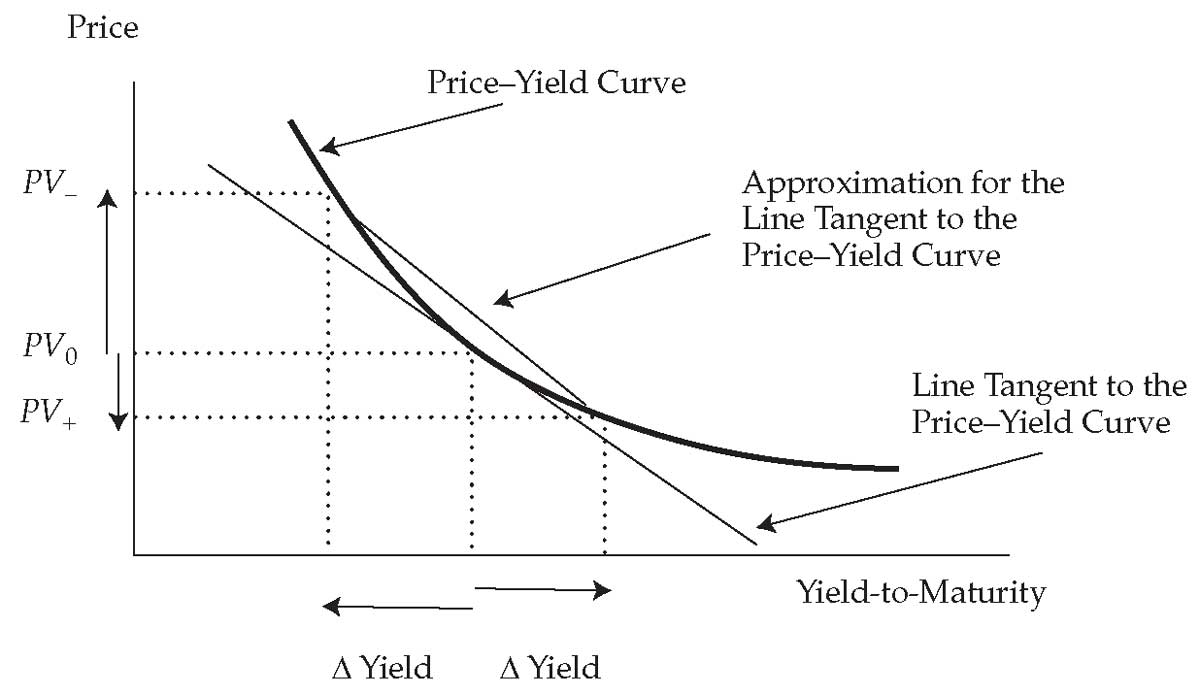
Приблизительная модифицированная дюрация.
Чтобы оценить наклон кривой, доходность к погашению увеличивается и уменьшается на то же значение - \(\Delta Yield\). После этого рассчитываются цены на облигацию с учетом новой доходности к погашению.
Цена, соответствующая увеличению доходности, обозначается как \(PV_+\). Цена, соответствующая уменьшению доходности, обозначается как \(PV_-\). Первоначальная цена обозначается как \(PV_0\). Эти цены являются полными ценами, включающими начисленные проценты. Наклон линии на основе \(PV_+\) и \(PV_-\) является приближением для наклона линии, касающейся кривой цены-доходности.
Следующий пример иллюстрирует высокую точность этого приближения. На самом деле, когда \(\Delta Yield\) стремится к нулю, приближение стремится к AnnModDur.
Рассмотрим облигацию с 6% полугодовым купоном, с погашением 14 февраля 2027 года. При расчете на 11 апреля 2019 года полная цена (\(PV_0\)) составляет 100.940423, с учетом того, что доходность к погашению составляет 6.00%.
\( \dst PV_0 = \left[ {3\over1.03^1}+ {3\over1.03^2}+ \ldots + {103\over1.03^{16}} \right]
\times 1.03^{57/180} = 100.940423 \)
Увеличим годовую доходность к погашению на 5 б.п., с 6.00% до 6.05%. Это увеличение соответствует увеличению доходности к погашению за полугодовой период на 2.5 б.п., с 3.00% до 3.025% за период. Новая полная цена (\(PV_+\)) составляет 100.631781.
\( \dst
PV_+ = \left[ {3\over1.03025^1}+ {3\over1.03025^2}+ \ldots + {103\over1.03025^{16}} \right] \times 1.03025^{57/180} = 100.631781 \)
Уменьшим годовую доходность к погашению на 5 б.п., с 6.00% до 5.95%. Это уменьшение соответствует уменьшение доходности к погашению за полугодовой период на 2.5 б.п., с 3.00% до 2.975% за период. Новая полная цена (\(PV_-\)) составляет 101.250227.
\( \dst
PV_- = \left[ {3\over1.02975^1}+ {3\over1.02975^2}+ \ldots + {103\over1.02975^{16}} \right] \times 1.02975^{57/180} = 101.250227 \)
Введем эти результаты в Формулу 7, чтобы рассчитать изменение годовой доходности к погашению на 5 б.п.: \(\Delta Yield\ = 0.0005:
\( \dst {\rm ApproxModDur}
= {101.250227-100.631781 \over 2\times 0.0005 \times 100.940423}
= 6.126842 \)
«Точная» годовая модифицированная дюрация для этой облигации составляет 6.126829, а «приближенная» - 6.126842. Это почти идентичные результаты.
Следовательно, хотя дюрацию можно рассчитать с использованием подхода, описанного в Иллюстрациях 2 и 3 (т.е., с помощью расчета средневзвешенного срока получения каждого денежного потока) или с использованием Формулы 4, его также можно оценить довольно точно с использованием базовой формулы оценки облигаций и финансового калькулятора.
Дюрацию Маколея также можно аппроксимировать - приблизительная модифицированная дюрация, умноженная на один плюс доходность за период.
\( \dst {\rm ApproxMacDur} = {\rm ApproxModDur} \times (1+r) \)
Формулы приближения дают результаты для аннуализированных (годовых) показателей модифицированной дюрации и дюрации Маколея. Частота купонных платежей и периодичность доходности к погашению включены в расчеты цены облигации.
Пример (8) расчета приблизительной модифицированной дюрации и приблизительной дюрации Маколея.
Предположим, что 3.75% казначейская гособлигация США, с погашением 15 августа 2041 года, оценивается с доходностью 5.14% при расчете на 15 октября 2020 года. Полугодовые купоны выплачиваются 15 февраля и 15 августа.
Доходность к погашению указана на основе «уличной конвенции» для подсчета дней, с полугодовым начислением. Дата урегулирования (расчета) приходится 61 день в 184-дневном периоде купона, с использованием конвенции «фактические/фактические дни» для подсчета дней.
Рассчитайте приблизительную модифицированную дюрацию и приблизительную дюрацию Маколея для этой казначейской облигации, предполагая изменение доходности на 5 б.п.
Решение:
Доходность к погашению за полугодовой период составляет 0.0257 (= 0.0514/2). Выплата купона за период составляет 1.875 (= 3.75/2). На начало периода срок погашения составляет 21 год (42 полугодовых периода).
Прошедшая часть периода составляет 61/184. Полная цена для этой доходности к погашению составляет 82.967530 на 100 ед. номинальной стоимости.
\( \dst
PV_0 = \left[ {1.875 \over 1.0257^1}+ {1.875 \over 1.0257^2}+ \ldots + {1.875 \over 1.0257^{42}} \right] \times 1.0257^{61/184} = 82.96753 \)
При увеличении доходности к погашению с 5.14% до 5.19%, или с 2.57% до 2.595% в полугодовом исчислении, цена составляет 82.411395 на 100 номинальной стоимости.
\( \dst
PV_+ = \left[ {1.875 \over 1.02595^1}+ {1.875 \over 1.02595^2}+ \ldots + {1.875 \over 1.02595^{42}} \right] \times 1.02595^{61/184} = 82.411395 \)
При уменьшении доходности к погашению с 5.14% до 5.09%, или с 2.57% до 2.545% в полугодовом исчислении, цена составляет 83.528661 на 100 номинальной стоимости.
\( \dst
PV_- = \left[ {1.875 \over 1.02545^1}+ {1.875 \over 1.02545^2}+ \ldots + {1.875 \over 1.02545^{42}} \right] \times 1.02545^{61/184} = 83.528661 \)
Приблизительная годовая модифицированная дюрация казначейской облигации составляет 13.466.
\( \dst {\rm ApproxModDur}
= {83.528661-82.411395 \over 2\times 0.0005 \times 82.967530} = 13.466 \)
Приблизительная годовая дюрация Маколея составляет 13.812.
\( \dst {\rm ApproxMacDur} = 13.466 \times 1.0257 = 13.812 \)
Таким образом, благодаря этому показателю, инвестор знает, что средневзвешенный срок получения процентов и основных платежей составит 13.812 года (дюрация Маколея) и что предполагаемый убыток рыночной стоимости облигации составит 13.466% (модифицированная дюрация), если рыночная ставка дисконтирования внезапно увеличится на 1%, с 5.14% до 6.14%.
