В предыдущем разделе мы рассмотрели дискретные случайные величины (например, случайные величины, множество возможных исходов которых счетно). В отличие от них, возможные исходы непрерывных случайных величин никогда не счетны.

Если, например, 1.250 является одним из возможных значений непрерывной случайной величины, то мы не можем назвать следующую более высокую или более низкую возможную величину. Технически, диапазон возможных исходов непрерывной случайной величины включает всю вещественную ось (т.е. все действительные числа между \( -\infty \) и \( +\infty \)) или некоторое подмножество вещественной оси.

В этом разделе мы сосредоточимся на двух наиболее важных непрерывных распределениях для инвестиционной и финансовой деятельности, нормальном и логнормальном.

Как и при рассмотрении дискретных распределений, мы начнем с равномерного распределения вероятности.

Непрерывное равномерное распределение вероятностей.

Непрерывное равномерное распределение (англ. 'continuous uniform distribution') является простейшим непрерывным распределением вероятностей. Равномерное распределение имеет два основных применения:

  1. Оно лежит основе методов для генерации случайных чисел. Равномерное распределение применяется в моделировании методом Монте-Карло.
  2. В качестве распределения вероятностей, которое описывает одинаково вероятные результаты, равномерное распределение является подходящей вероятностной моделью для представления определенного рода неопределенности в ситуациях, в которых все результаты появляются с равной вероятностью.

Функция плотности распределения вероятностей (или pdf, от англ. 'probability density function') для равномерной случайной величины:

\( \dst f(x)= \begin{cases}
& \dst {1 \over b-a} {\small \text{ при }} a < x < b \\[1ex]
& 0 {\small \text{ в противном случае} }
\end{cases} \)

Например, при \( а = 0 \) и \( b = 8 \), \( f(x) = 1/8 \) или 0.125. График этой плотности распределения изображен на Рисунке 3.

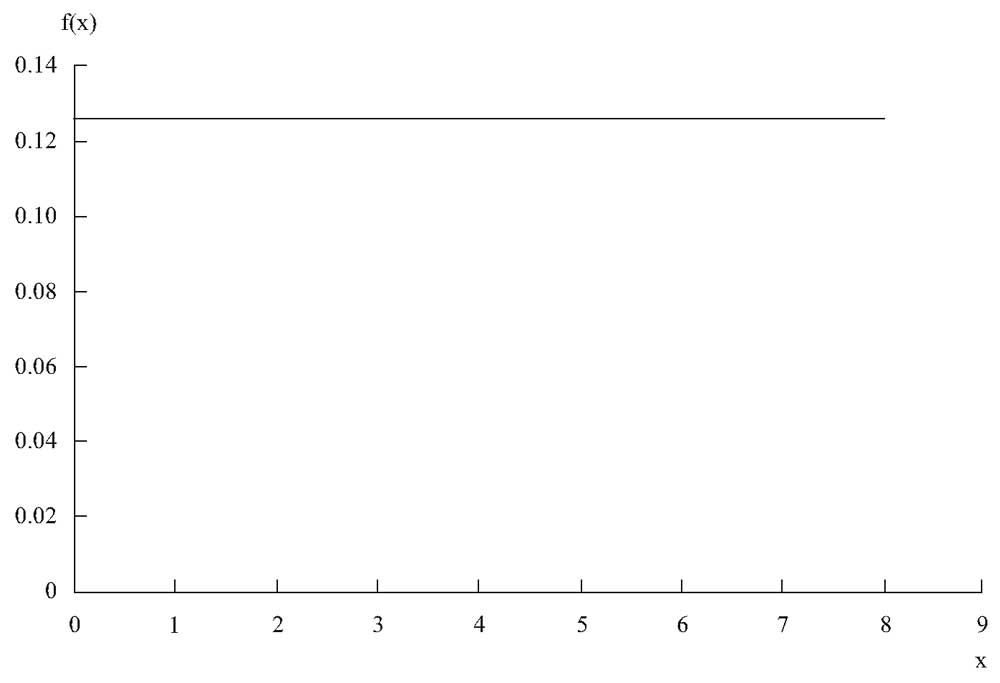Рисунок 3. Непрерывное равномерное распределение. Рисунок 3. Непрерывное равномерное распределение.

График функции плотности распределения представлен в виде горизонтальной линии со значением 0.125.

Какова вероятность того, что равномерная случайная величина в интервале \( а = 0 \) и \( b = 8 \) будет меньше или равна 3, или \( F(3) = P(X \leq 3) \)?

Когда мы работали с дискретной равномерной случайной величиной с возможными результатами 1, 2, ..., 8, мы просто суммировали отдельные вероятности: \( р(1) + р(2) + р(3) = 0.375 \).

В противоположность этому, вероятность того, что непрерывная равномерная случайная величина или любая непрерывная случайная величина принимает любое заданное фиксированное значение равно 0.

Чтобы проиллюстрировать это, рассмотрим узкий интервал от 2.510 до 2.511.

Поскольку интервал имеет бесконечное множество возможных значений, сумма вероятностей значений в одном только этом отрезке будет бесконечной, если каждое отдельное значение в ней имело положительную вероятность. Чтобы найти вероятность \( F(3) \), находим площадь под кривой графика плотности распределения, в диапазоне от 0 до 3 на оси \(x\).

Эта операция называется интегрированием функции вероятности \( f(x) \) от 0 до 3. Эта область под кривой представляет собой прямоугольник с основанием 3 - 0 = 3 и высотой 1/8. Площадь этого прямоугольника равна произведению основания на высоту: \( 3(1/8) = 3/8 \) или 0.375. Таким образом, \( F(3) = 3/8 \) или 0.375.

Интервал от 0 до 3 составляет три восьмые общей длины в пределах от 0 до 8, и \( F(3) \) составляет три восьмых общей вероятности 1. Средняя строка в выражении кумулятивной функции распределения (cdf) содержит эту связь.

\( \dst f(x)= \begin{cases}
& \dst 0 {\small \text{ при }} x \leq a  \\[1ex]
& \dst {x-a \over b-a} {\small \text{ при }} a < x < b \\[1ex] 
& \dst 0 {\small \text{ при }} x \geq b  \end{cases} \)

Для нашей задачи, \( F(х) = 0 \) при \( х \leq 0 \), \( F(х) = х/8 \) при \( 0 <х <8 \) и \( F(х) = 1 \) при \( х \geq 8 \).

График этой кумулятивной функции распределения изображен на Рисунке 4.

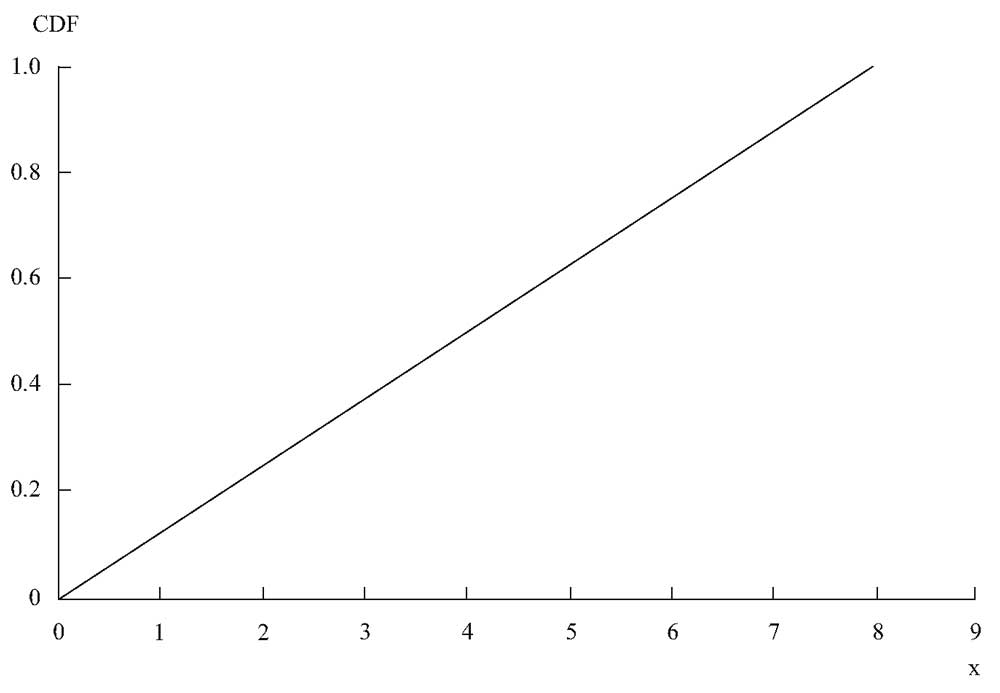Рисунок 4. Функция непрерывного равномерного распределения вероятностей. Рисунок 4. Функция непрерывного равномерного распределения вероятностей.

Математическая операция, которая соответствует нахождению площади под кривой \( f(x) \) от a до b, есть интеграл \( f(x) \) от a до b:

\( \large \dst Р(а \leq X \leq b) = \int_{a}^{b} f(x)dx \) (Формула 2)

где

  • \( \int dx \) является символом для суммирования \( \int \) малых изменений \( dx \), а пределы интегрирования (a и b) могут быть любыми действительными числами от \( -\infty \) до \( +\infty \).

Все вероятности непрерывных случайных величин могут быть вычислены с использованием Формулы 2.

Для примера равномерного распределения, рассмотренного выше, \( F(7) \) рассчитывается по Формуле 2 с нижним пределом \( а = 0 \) и верхним пределом \( b = 7 \). Интеграл, соответствующий функции равномерного распределения сводится к выражению в три строки, приведенному выше.

Для того, чтобы сделать расчет по Формуле 2 для практически всех других непрерывных распределений, включая нормальное и логнормальное, мы полагаемся на электронные таблицы, компьютерные программы или таблицы значений для вычисления вероятностей. Эти инструменты используют различные численные методы для вычисления интеграла в Формуле 2.

Напомним, что вероятность непрерывной случайной величины, соответствующей любой фиксированной точке, равна 0.

Этот факт имеет важное значение для работы с кумулятивной функцией распределения непрерывной случайной величины:

Для любой непрерывной случайной величины \( X \), \( P(a \leq X \leq b) \) \(=  P(a < X  \leq b) \) \(= P(a \leq X < b) \) \( = P(a < X < b) \), так как вероятности в конечных точках a и b равны 0.

Для дискретных случайных величин эти отношения равенства не являются истинными, поскольку вероятность скапливается в точках.

Пример (7) расчета вероятности нарушения ковенантов по кредитной линии.

Вы оцениваете облигации заемщика, не получившего инвестиционного класса, в нижней точке в его бизнес-цикла. Вам нужно рассмотреть множество факторов, в том числе условия банковского кредитования компании.

Договоры банковского кредитования, такие как необеспеченная кредитная линия, как правило, содержат условия, известные как ковенанты (англ. 'covenant').

См. также:

CFA - Долговые ковенанты.

Эти ковенанты налагают ограничения на действия заемщика. Компания нарушит ковенант кредитной линии, если коэффициент покрытия процентов, EBITDA / проценты, рассчитанный по EBITDA за четыре последних квартала, окажется ниже 2.0.

Показатель EBITDA представляет собой прибыль до вычета процентов, налогов, износа и амортизации. (см. также: EBITDA: Работает ли по-прежнему этот показатель?)

Соблюдение ковенантов будет проверяться в конце текущего квартала. Если окажется, что ковенант нарушен, банк может потребовать от компании немедленного погашения всей задолженности по кредитной линии. Подобная ситуация действие, вероятно, приведет компанию к кризису ликвидности.

С высокой степенью уверенности, вы прогнозируете процентные расходы в размере $25 млн. Ваша оценка EBITDA варьируется от $40 млн. в худшем случае до $60 млн. в лучшем случае.

Вам необходимо ответить на два вопроса (рассматривающих прогнозируемые процентные платежи в качестве константы):

  1. Если результаты по EBITDA равновероятны, какова вероятность того, что EBITDA / проценты упадет ниже 2.0, нарушив ковенант?
  2. Расчитайте среднее и стандартное отклонение коэффициента EBITDA/проценты. Для непрерывной равномерной случайной величины, среднее определяется как \( \mu = (а+b)/2 \), а дисперсия определяется как \( \sigma^2 = (b-a)^2 / 12 \).

Решение для части 1:

Соотношение EBITDA/проценты является непрерывной равномерной случайной величиной, так как все результаты одинаково вероятны. Соотношение может принимать значения между 1.6 = ($40 млн.) / ($25 млн.) в нижнем пределе и 2.4 = ($60 млн. / $25 млн.) в верхнем пределе.

Диапазон возможных значений составляет: 2.4 - 1.6 = 0.8.

Какая часть возможных значений окажется ниже уровня 2.0, который приведет к дефолту кредитной линии?

Промежуток между 2.0 и 1.6 составляет 0.40. Значение 0.40 составляет половину общей длины 0.8, или 0.4 / 0.8 = 0,50. Таким образом, вероятность того, что ковенант будет нарушен, составляет 50%.

Решение для части 2:

В решении для части 1, мы обнаружили, что нижний предел коэффициента EBITDA/проценты равен 1.6. Этот нижний предел является \( a \). Мы обнаружили, что верхний предел составляет 2.4. Этот верхний предел является \( b \). Используя формулы, приведенные выше, находим среднее:

\( \mu = (а+b)/2 = (1.6 + 2.4)/2 = 2.0 \)

Дисперсия коэффициента покрытия процентов будет равна:

\( \sigma^2 = (b-a)^2 / 12 = (2.4 - 1.6)^2/12 = 0.053333 \)

Стандартное отклонение представляет собой положительный квадратный корень из дисперсии, \( 0.230940 = (0.053333)^{1/2} \). Однако, стандартное отклонение не является особенно полезным в качестве меры риска для равномерного распределения.

Вероятность, лежащая в различных интервалах стандартного отклонения вокруг среднего чувствительна к различным значениям верхних и нижних пределов (хотя неравенство Чебышева всегда выполняется).

Неравенство Чебышева обсуждается в чтении о статистических концепциях и доходности рынка (см. CFA - Неравенство Чебышева).

Здесь, один интервал стандартного отклонения интервала вокруг среднего значения 2.0 варьируется от 1.769 до 2.231 и охватывает 0.462/0.80 = 0.5775 или 57.8 процентов вероятности. Второй интервал стандартных отклонений варьируется от 1.538 до 2.462, и охватывает оба предела случайной величины.