Логнормальное распределение вероятностей тесно связано с нормальным распределением и широко используется для моделирования распределения вероятностей цен на акции и другие активы. Например, логнормальное распределение применяется в модели ценообразования опционов Блэка-Шоулза-Мертона.

Модель Блэка-Шоулза-Мертона (англ. 'Black-Scholes-Merton option pricing model') предполагает, что цена актива, лежащего в основе опциона, логнормально распределяется.

Случайная величина \( Y \) следует логнормальному распределению (англ. 'lognormal probability distribution'), если ее натуральный логарифм, \( \ln{Y} \), имеет нормальное распределение.

Верно и обратное: если натуральный логарифм случайной величины \(Y \), \( \ln{Y} \), имеет нормальное распределение, то \( Y \) следует логнормальному распределению. Если вы думаете о термине «логнормальный» как о «логарифмически нормальном», то у вас не будет проблем с запоминанием его смысла.

Два наиболее примечательных свойства логнормального распределения заключаются в том, что оно ограничено снизу 0 и имеет перекос вправо (т.е. имеет длинный правый хвост). Обратите внимание на эти два свойства на графиках двух логнормальных распределений на Рисунке 7.

Цены на активы ограничены снизу 0. На практике было установлено, что логнормальное распределение довольно точно описывает распределение цен на многие финансовые активы.

С другой стороны, нормальное распределение часто является хорошей приблизительной моделью для доходности активов. По этой причине оба эти распределения очень важны для профессионалов в области финансов.

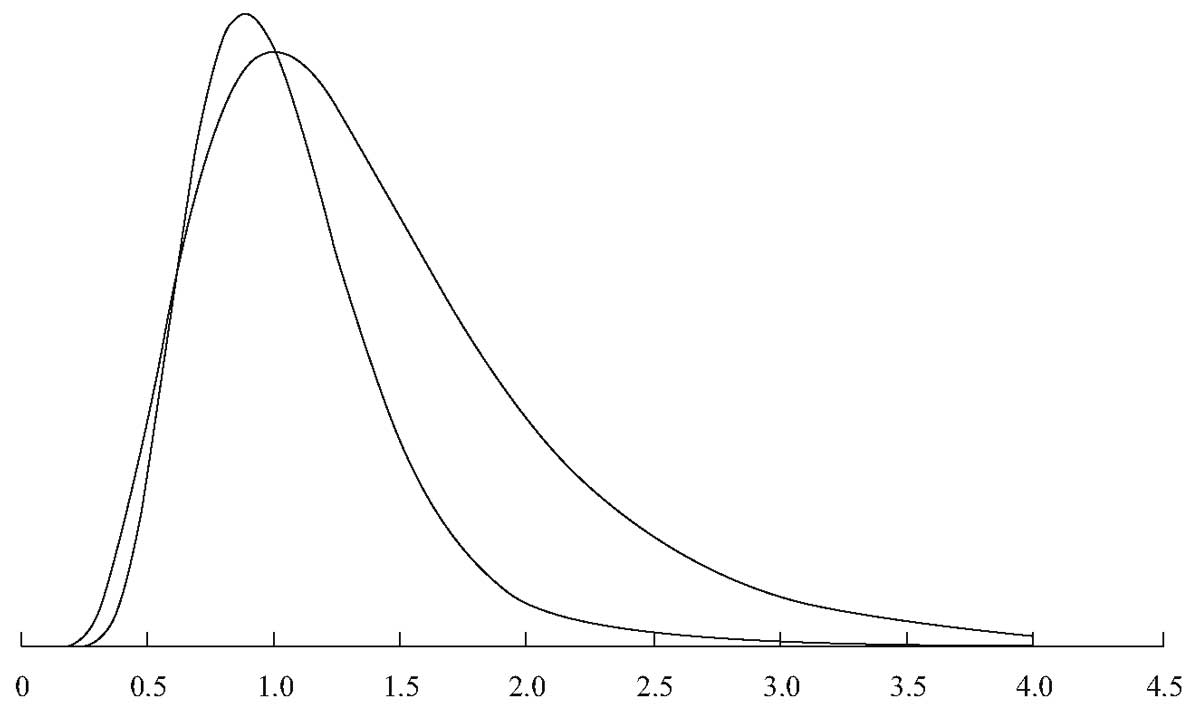Рисунок 7. Два логнормальных распределения. Рисунок 7. Два логнормальных распределения.

Подобно нормальному распределению, логнормальное распределение полностью описывается двумя параметрами. В отличие от других распределений, которые мы рассмотрели, логнормальное распределение определяется в терминах параметров иного распределения.

Два параметра логнормального распределения - это среднее и стандартное отклонение (или дисперсия) связанного с ним нормального распределения: среднее значение и дисперсия \( \ln{Y} \), при условии, что величина \( Y \) логнормальна.

Помните, мы должны следить за двумя наборами средних и стандартных отклонений (или дисперсий):

  • среднее значение и стандартное отклонение (или дисперсия) связанного нормального распределения (это параметры), и
  • среднее значение и стандартное отклонение (или дисперсия) самой логнормальной случайной величины.

Выражения для среднего и дисперсии самой логнормальной величины сложны.

Предположим, что нормальный случайная величина \(X\) имеет ожидаемое значение \( \mu \) и дисперсию \( \sigma^2 \).

Определим \( Y = \exp (X) \). Помните, что экспоненциальная функция может обозначаться как \( \exp (X) \) или \( e^X \), и является операцией, обратной логарифму. Величина \( e \approx 2.7182818 \).

Поскольку величина \( Y = \ln [ \exp (X)] = X \) нормально (мы предполагаем, что \(X\) нормально), величина \(Y\) является логнормальной.

Что представляет собой ожидаемое значение \( Y = \exp (X) \)?

Можно предположить, что ожидаемое значение \(Y\) это \( \exp(\mu) \). На самом деле, ожидаемое значение - это \( \exp(\mu + 0.50\sigma^2) \), что больше, чем \( \exp(\mu) \) на коэффициент \( \exp(0.50\sigma^2) > 1 \).

Заметим, что \( \exp(0.50\sigma^2) > 1 \), потому что \( \sigma^2 > 0 \).

Чтобы получить некоторое представление об этой концепции, подумайте о том, что произойдет, если мы увеличим \( \sigma^2 \). Распределение расширяется; оно может расширяться вверх, но он не может расширяться вниз ниже 0. В результате, центр распределения выталкивается вправо - среднее распределения увеличивается.

Источник этого объяснения: Luenberger (1998).

Выражения для среднего значения и дисперсии логнормальной случайной величины приведены ниже, где \( \mu \) и \( \sigma^2 \) - среднее и дисперсия соответствующего нормального распределения.

Обращайтесь к этим выражениям по мере необходимости, если нет потребности запоминать их:

  • Среднее (\( \mu_L \)) логнормальной случайной величины \( =\exp (\mu + 0.50\sigma^2) \)
  • Дисперсия (\( \sigma_L^2 \)) логнормальной случайной величины \( =\exp (2\mu + \sigma^2) \times [ \exp (\sigma^2) - 1] \)

Теперь мы исследуем взаимосвязь между распределением доходности акций и ценой акций. Далее мы покажем, что если непрерывно начисляемая (т.е. по сложной ставке) доходность акций имеет нормальное распределение, то будущая цена акций будет обязательно логнормально распределена.

Непрерывное начисление означает непрерывную или сплошную временную линию, в отличии от дискретного начисления, при котором время движется в дискретных конечных интервалах.

Непрерывно начисляемая доходность - это одна из так называемых моделей непрерывного финансирования (англ. 'continuous time finance model'), таких как модель ценообразования опционов Блэка-Шоулза-Мертона.

См. чтения о временной стоимости денег для получения дополнительной информации о непрерывном (сложном) начислении процентов.

Кроме того, мы покажем, что цену акций можно хорошо описать логнормальным распределением, даже если непрерывно начисляемая доходность не следует нормальному распределению. Эти результаты дают теоретическую основу для моделирования цен с помощью логнормального распределения.

Сначала мы покажем, что цена акций в будущий момент времени \(T\), \( S_T \), равна текущей цене акций, \( S_0 \), умноженной на \(e\), возведенной в степень \( r_{0,T}\), что означает непрерывно начисляемую доходность за временной промежуток от \(0\) до \(T\).

Это соотношение выражается как:

\( S_T = S_0 \exp (r_{0,T}) \)

Мы можем записать \( r_{0,T}\) как сумму непрерывно начисляемой доходности за более короткие временные периоды, и, если доходность за короткие периоды нормально распределена, то \( r_{0,T}\) тоже нормально распределена (при определенных допущениях) или приближенно нормально распределена (без этих допущений).

Так как цена \( S_T \) пропорциональна логарифму нормальной случайной величины, \( S_T \) является логнормальной.

Для того, чтобы создать основу для дальнейшего обсуждения, предположим, что мы имеем ряд последовательных наблюдений стоимости акций (через равные временные периоды):

\( S_0, S_1, S_2, \ldots , S_T \)

Текущая цена акций, \( S_0 \), является известной величиной и поэтому неслучайна. Будущие цены (например, \( S_1 \)), однако, являются случайными величинами.

Относительная цена (англ. 'price relative'), \( S_1 / S_0 \), является отношением конечной цены \( S_1 \) к начальной цене \( S_0 \). Она равна 1 плюс ставка доходности за  период владения акцией от \(t=0\) до \(t=1\):

\( S_1 / S_0 = 1 + R_{0,1} \)

Например, если \(S_0 = \$30\) и \(S_1 = \$34.50 \), то \( S_1 / S_0 = \$34.50 / \$30 = 1.15\). Поэтому, \( r_{0,1} = 0.15 \) или 15%.

В целом, относительные цены имеют вид:

\( S_{t+1} / S_t = 1 + R_{t,t+1} \)

где

  • \(R_{t,t+1} \) - ставка доходности за период от \( t \) до \( t+1 \).

Непрерывно начисляемая доходность.

Важной концепцией является непрерывно начисляемая доходность, связанная с доходностью за период владения, такой как \( R_{0,1} \).

Непрерывно начисляемая доходность (англ. 'continuously compounded return'), связанная с доходностью за период владения, это натуральный логарифм из 1 плюс эта доходность за период владения, или, что эквивалентно, натуральный логарифм из конечной цены деленной на начальную цену (относительная цена).

В этом чтении мы используем строчную \(r\) для обозначения именно непрерывно начисляемой доходности.

Например, если мы наблюдаем недельную доходность за период владения 0.04, то недельной непрерывно начисляемой доходностью является \( \ln (1.04) = 0.039221 \).

€1.00 инвестированный на одну неделю под 0.039221 при непрерывном начислении приносит €1.04, что эквивалентно 4%-ной недельной доходности за период владения.

Формула непрерывно начисляемой доходности для временного промежутка от \( t \) до \( t+1 \):

\( \large \dst r_{t,t+1} = \ln (S_{t+1} / S_t) = \ln (1 + R_{t,t+1}) \) (Формула 5)

В нашем примере, 

\( \begin{aligned}
r_{0,1} &= \ln(S_1/S_0) \\
&= \ln (1 + R_{0,1}) = \ln (\$34.50/$30) \\
&= \ln(1.15) =  0.139762
\end{aligned} \)

Таким образом, ставка 13.98% является непрерывно начисляемой доходностью во временной промежуток от \( t=0 \) до \( t=1 \). Непрерывно начисляемая доходность меньше соответствующей доходности за период владения.

Если наш инвестиционный временной горизонт простирается от \( t=0 \) до \( t=T \), то непрерывно начисляемая доходность в момент времени \( T \) будет:

\( r_{0,T} = \ln (S_T / S_0) \)

Применив экспоненциальную функцию к обеим сторонам уравнения, мы получим:

\( \exp(r_{0,T}) = \exp[ \ln (S_T / S_0)] = S_T / S_0 \),

поэтому

\( S_T = S_0 \exp (r_{0,T}) \)

Мы также можем выразить \( S_T / S_0 \) как произведение относительных цен:

\( S_T / S_0 = (S_T / S_{T-1}) (S_{T-1} / S_{T-2}) \ldots (S_1 / S_0)  \)

Логарифмируя обе стороны этого уравнения, мы находим, что непрерывно начисляемая доходность к моменту времени \( Т \) равна сумме ставок непрерывно начисляемой доходности за 1 период:

\( \large \dst
r_{0,T} = r_{T-1,T} + r_{T-2,T-1} + \ldots  \ r_{0,1} \) (Формула 6)

Использование доходности за период владения для нахождения конечного значения $1 инвестиции, предполагает умножение величин (1 + доходность за период владения). Использование же непрерывно начисляемой доходности предполагает сложение.

Ключевом предположением во многих инвестиционных задачах является то, что ставки доходности независимо и идентично распределены (IID, от англ. 'independently and identically distributed'):

  • Независимость отражает предположение о том, что инвесторы не могут предсказать будущую доходность, используя прошлую доходность (то есть, это слабая степень эффективности рынка, от англ. 'weak-form market efficiency').
  • Идентичное распределение отражает предположение о стационарности (то есть, неизменности во времени). Стационарность подразумевает, что среднее и дисперсия доходности не изменяются от периода к периоду.

Предположим, что ставки непрерывно начисляемой доходности за 1 период (например, \( r_{0,1} \)) являются IID случайными величинами со средним \( \mu \) и дисперсией \( \sigma^2 \) (но не делаем предположение о нормальности или других предположений о характере распределения), тогда

\( \large \dst \begin{aligned}
{E(r_{0,T})} &= E(r_{T-1,T}) + E(r_{T-2,T-1}) \\ &+ \ldots  E(\ r_{0,1}) = \mu T
\end{aligned} \) (Формула 7)

(мы складываем \( \mu \) в общей сложности \( T \) раз) и

\( \large \dst \sigma^2(r_{0,T}) = \sigma^2 T \) (Формула 8)

(как следствие предположения о независимости).

Дисперсия непрерывно начисляемой доходности за период владения \( T \) равна \( T \), умноженному на дисперсию непрерывно начисляемой доходности за 1 период. Кроме того:

\( \sigma(r_{0,T}) = \sigma \sqrt{T} \)

Если непрерывно начисляемая доходность за 1 период в правой части Формулы 6 нормально распределяется, то непрерывно начисляемой доходности за период владения \( T \) , \( r_{0,T} \), также нормально распределяется со средним \( \mu T \) и дисперсией \( \sigma^2 T \).

Эта связь объясняется тем, что линейная комбинация нормальных случайных величин тоже нормальна. Но даже если ставки непрерывно начисляемой доходности за 1 период не являются нормальными, их сумма, \( r_{0,T} \), является приближенно нормальной в соответствии с центральной предельной теоремой.

Мы упоминали центральную предельную теорему (англ. 'central limit theorem') ранее, при обсуждении нормального распределения.

Напомним, что в соответствии с центральной предельной теоремой сумма (а также среднее) множества независимых идентично распределенных случайных величин с конечными дисперсиями нормально распределяется, независимо от распределения самих случайных величин.

Центральная предельная теорема обсуждается далее в чтениях о выборочном методе.
[см.: CFA - Центральная предельная теорема и распределение выборочного среднего]

Теперь сравните \( S_T = S_0 \exp (r_{0,T}) \) с \(Y = \exp(Х) \), где \( Х \) является нормальной и Y является логнормальной (как обсуждалось выше).

Ясно, что мы можем моделировать будущую цену акций \( S_T \) как логнормальную случайную величину, поскольку \( r_{0,T} \) должна быть по крайней мере, приблизительно нормально распределена.

Это предположение о нормально распределенной доходности является основой в теории применения логнормального распределения в качестве модели для распределения цен на акций и другие активы.

Волатильность.

Непрерывно начисляемая доходность играет роль во многих моделях ценообразования опционов, как уже упоминалось ранее. Оценка волатильности имеет решающее значение для использования моделей ценообразования опционов, таких как модель Блэка-Шоулза-Мертона.

Волатильность (англ. 'volatility') оценивает стандартное отклонение непрерывно начисляемой доходности базового актива.

Волатильность также называют мгновенным стандартным отклонением, и обозначают так же: \( \sigma \). Базовый актив в данном случае - это актив, лежащий в основе опциона.

Для получения более подробной информации об этих концепциях см. Chance and Brooks (2012).

На практике мы очень часто оцениваем волатильность, используя историческую последовательность непрерывно начисляемой дневной доходности. Мы собираем множество ставок непрерывно начисляемой доходности (за период владения 1 день), и затем используем Формулу 5, чтобы преобразовать их в непрерывно начисляемую дневную доходность.

Затем мы вычисляем стандартное отклонение непрерывно начисляемой дневной доходности и аннуализируем (пересчитываем в годовое исчисление) это значение с помощью Формулы 8.

Для вычисления стандартного отклонения множества или выборки из \(n\) ставок доходности, мы суммируем квадраты отклонения каждой ставки доходности от средней доходности, а затем делим эту сумму на \( n - 1 \) (см. Формулу 13 ). В результате получается выборочная дисперсия.

Квадратный корень из выборочной дисперсии дает нам стандартное отклонение выборки. Более подробно расчет стандартного отклонения рассмотрен в чтениях о статистических концепциях и доходности рынка.

По соглашению, волатильность указывается в годовом исчислении.

В финансовой практике годовое исчисление часто рассчитывается на базе 250 дней в году - это приблизительное количество дней, когда финансовые рынки открыты для торговли. База в 250 дней в году может привести к лучшей оценке волатильности, чем календарная база - в 365 дней.

Таким образом, если дневная волатильность была 0.01, мы можем выразить волатильность (в годовом исчислении) как \( 0.01 \sqrt{250} = 0.1581 \).

Пример 10 иллюстрирует оценку волатильности акций Astra International.

Пример (10) оценки волатильности в соответствии с моделью ценообразования опционов.

Предположим, вы анализируете акции компании Astra International (обозначение на индонезийской фондовой бирже: ASII) и вас интересует цена акций Astra за неделю, в течение которой международные экономические новости существенно повлияли на индонезийский фондовый рынок.

Вы решили использовать волатильность в качестве меры изменчивости акций Astra в течение этой недели. Таблица 7 показывает цены закрытия (цены на момент закрытия биржи) в течение этой недели.

Таблица 7. Ежедневные цены закрытия акций Astra International.

Дата

Цена закрытия (IDR)

17 июня 2013

6,950

18 июня 2013

7,000

19 июня 2013

6,850

20 июня 2013

6,600

21 июня 2013

6,350

Используйте данные из Таблице 7, чтобы сделать следующее:

  1. Оцените волатильность акций Astra. (Пересчитайте волатильность в годовое исчисление на основе 250 дней в году.)
  2. Определите распределение вероятностей для цен на акции Astra, если непрерывно начисляемая дневная доходность следует нормальному распределению.

Решение для части 1:

Во-первых, используйте Формулу 5 для расчета непрерывно начисляемой дневной доходности. Затем найдите стандартное отклонение для полученной доходности обычным способом. (При расчете выборочной дисперсии, чтобы получить стандартное отклонение выборки, используйте в знаменателе размер выборки, уменьшенный на 1).

\( \ln(7,000/6,950) = 0.007168 \)
\( \ln(6,850/7,000) = -0.021661 \)
\( \ln(6,600/6,850) = -0.037179 \)
\( \ln(6,350/6,600) = -0.038615 \)

Сумма = -0.090287
Среднее = -0.022572
Дисперсия = 0.000452
Стандартное отклонение = 0.021261

Стандартное отклонение непрерывно начисляемой дневной доходности равно 0.021261.

Формула 8 утверждает, что \( \hat{\sigma} (r_{0,T}) = \hat{\sigma} \sqrt{T} \). В этом примере \( \hat{\sigma} \) является стандартным отклонением выборки для непрерывно начисляемой доходности за 1 период. Таким образом, \( \hat{\sigma} \) соответствует 0.021261.

Мы хотим пересчитать результат в годовое исчисление так, чтобы временной горизонт \( T \) соответствовал одному году. Так как \( \hat{\sigma} \) исчисляется в днях, мы устанавливаем \( T \) равным количеству торговых дней в году (250).

Мы находим, что в годовом исчислении волатильность акций Astra за эту неделю составляла 33.6%, что рассчитывается как \( 0.02126 \sqrt{250} = 0.336165 \).

Обратите внимание, что выборочное среднее, -0.022572, является возможной оценкой среднего значения, \( \mu \), для непрерывно начисляемой доходности за 1 период или ставок дневной доходности.

Выборочное среднее может быть переведено в оценку ожидаемой непрерывно начисляемой годовой доходности с помощью Формулы 7: \( \hat{\mu} T = -0.022572 (250) \) (используется база в 250 дней, чтобы результат соответствовал расчету волатильности).

Но четырех наблюдений слишком мало, чтобы оценить ожидаемую доходность. Изменчивость дневной доходности важнее любой информации об ожидаемой доходности в такой короткой последовательности наблюдений.

Решение для части 2:

Цены на акции Astra должны следовать логнормальному распределению, если непрерывно начисляемая дневная доходность акций Astra следует нормальному распределению.

Мы показали, что распределение цены акций является логнормальным, с учетом некоторых предположений.

Каковы среднее значение и дисперсия \( S_T \), если \( S_T \) следует логнормальному распределению?

Выше мы привели перечень выражений для среднего и дисперсии логнормальной случайной величины. В этом перечне, \( \hat{\mu} \) и \( \hat{\sigma} \) ссылаются, в контексте этого обсуждения, на среднее и дисперсию временного горизонта \( T\) (а не одного периода) непрерывно начисляемой доходности (предполагая, что оно следует нормальному распределению), совместимому с временным горизонтом  \( S_T \).

Например, выражение для среднего значения:

\( E(S_T) S_0 \exp[E(r_{0,T}) + 0.5\sigma^2(r_{0,T})] \).

Ранее в этом чтении мы использовали среднее значение и дисперсию (или стандартное отклонение), чтобы построить интервалы, в которых мы ожидали найти определенный процент наблюдений нормально распределенной случайной величины. Эти интервалы были симметричны относительно среднего значения.

См. также:

CFA - Нормальное распределение вероятностей.

Можем ли мы использовать подобные, симметричные интервалы для логнормальной случайной величины?

К сожалению, мы не можем. Поскольку логнормальное распределение не является симметричным, такие интервалы являются более сложными, чем для нормального распределения, и мы не будем обсуждать эту особую тему здесь.

См. Hull (2011) для обсуждения логнормальных доверительных интервалов.

Наконец, мы представили связь между средним и дисперсией непрерывно начисляемой доходности с различными временными горизонтами (см. Формулы 7 и 8), но как связаны средние и дисперсии ставок доходности за период владения и ставок непрерывно начисляемой доходности?

Как аналитики, мы обычно рассуждаем в терминах доходности за период владения, а не непрерывно начисляемой доходности, и хотим преобразовать средние и стандартные отклонения доходности за период владения в средние и стандартные отклонения непрерывно начисляемой доходности для работы с опционами, например.

Чтобы осуществить такие преобразования (и в таком и в обратном направлении), мы можем использовать выражения, изложенные в работе: Ferguson (1993).