CFA - Инвестиционный горизонт, дюрация Маколея и риск процентных ставок
Рассмотрим взаимосвязь инвестиционного горизонта, дюрации Маколея и риска процентных ставок, - в рамках изучения ценных бумаг с фиксированным доходом по программе CFA.
Хотя риск краткосрочных процентных ставок является проблемой для некоторых инвесторов, прочие инвесторы имеют долгосрочный инвестиционный горизонт.
Ежедневные изменения цен на облигации приводят к нереализованному приросту и убытку капитала, и эти нереализованные прибыли и убытки могут быть отражены в финансовой отчетности.
Далее мы рассматриваем долгосрочного инвестора, заинтересованного только в общей прибыли в рамках инвестиционного горизонта. Для такого инвестора важен риск процентных ставок. Инвестор сталкивается с риском реинвестирования купонов, а также риском рыночной цены, если облигацию необходимо продать до погашения.
Ранее мы обсуждали примеры риска процентных ставок с использованием 10-летней облигации с 8% годовым купоном, оцениваемой в 85.503075 на 100 д.е. номинальной стоимости. Доходность к погашению облигации составляет 10.40%.
Ключевым результатом в Примере 3 является то, что инвестору с 10-летним инвестиционным горизонтом важен только риск реинвестирования купонов. Эта ситуация предполагает, конечно, что эмитент своевременно выплачивает все купоны и основные платежи.
Долгосрочный инвестор получает более высокую общую прибыль, если процентные ставки растут (см. Пример 3) и более низкую общую прибыль, если ставки падают (см. Пример 5).
В Примерах 4 и 6 инвестор имеет 4-летний горизонт. Этот инвестор сталкивается с риском рыночной цены (англ. 'market price risk') в дополнение к риску реинвестирования купонов. Фактически, риск рыночной цены доминирует, потому что этот инвестор имеет более высокую общую доходность, если процентные ставки падают (см. Пример 6) и более низкую доходность, если ставки растут (см. Пример 4).
Теперь рассмотрим третьего инвестора с 7-летним инвестиционным горизонтом. Если процентные ставки остаются на уровне 10.40%, будущая стоимость реинвестированных купоных процентов составляет 76.835787 на 100 д.е. номинальной стоимости.
\( \begin{aligned} \dst
&\big[ 8 \times (1.1040)^6 \big] + \big[ 8 \times (1.1040)^5 \big] + \big[ 8 \times (1.1040)^4 \big] + \big[ 8 \times (1.1040)^3 \big] + \\
&\big[ 8 \times (1.1040)^2 \big] + \big[ 8 \times (1.1040)^1 \big] + 8 = 76.835787
\end{aligned} \)
Облигация продается по цене 94.073336. Это предполагает, что облигация остается на траектории цены постоянной доходности и «стремится к номиналу».
\( \dst
{8 \over 1.1040^1} + {8 \over 1.1040^2} + {108 \over 1.1040^3} = 94.073336
\)
Общая прибыль составляет 170.909123 (= 76,835787 + 94.073336) на 100 д.е. номинала, а доходность горизонта, как и ожидалось, составляет 10.40%.
\( \dst 85.503075 = {170.909123 \over (1 + r)^7 } \), \(r = 0.1040 \)
Основываясь на Примерах 3 и 4, предположим, что доходность к погашению облигации увеличивается до 11.40%. Кроме того, купоны реинвестируются каждый год под 11.40%. Будущая стоимость реинвестированных купонов составляет 79.235183 на 100 д.е. номинальной стоимости.
\( \begin{aligned} \dst
&\big[ 8 \times (1.1140)^6 \big] + \big[ 8 \times (1.1140)^5 \big] + \big[ 8 \times (1.1140)^4 \big] + \big[ 8 \times (1.1140)^3 \big] + \\
&\big[ 8 \times (1.1140)^2 \big] + \big[ 8 \times (1.1140)^1 \big] + 8 = 79.235183
\end{aligned} \)
После получения седьмого купонного платежа облигация продается. Это означает убыток капитала, потому что цена продажи, хоть и намного выше, чем цена покупки, оказывается ниже траектории цены постоянной доходности.
\( \dst {8 \over 1.1140^1} + {8 \over 1.1140^2} + {108 \over 1.1140^3} = 91.748833 \)
Общая прибыль составляет 170.984016 (= 79.235183 + 91.748833) на 100 д.е. номинальной стоимости, а ставка доходности - 10.407%.
\( \dst 85.503075 = {170.984016 \over (1 + r)^7 } \), \(r = 0.10407 \)
Основываясь на Примерах 5 и 6, предположим, что ставки реинвестирования купона и доходность к погашению облигации снижаются до 9.40%. Будущая стоимость реинвестированных купонов составляет 74,512177.
\( \begin{aligned} \dst
&\big[ 8 \times (1.10940)^6 \big] + \big[ 8 \times (1.10940)^5 \big] + \big[ 8 \times (1.10940)^4 \big] + \big[ 8 \times (1.10940)^3 \big] + \\
&\big[ 8 \times (1.10940)^2 \big] + \big[ 8 \times (1.10940)^1 \big] + 8 = 74.52177
\end{aligned} \)
Облигация продается с приростом капитала, потому что цена превышает траекторию траектории цены постоянной доходности.
\( \dst {8 \over 1.10940^1} + {8 \over 1.10940^2} + {108 \over 1.10940^3} = 96.481299 \)
Общая прибыль составляет 170.993476 (= 74.512177 + 96.481299) на 100 д.е. номинальной стоимости, а доходность инвестиционного горизонта составляет 10.408%.
\( \dst 85.503075 = {170.993476 \over (1 + r)^7 } \), \(r = 0.10408 \)
Эти результаты обобщены в следующей таблице, чтобы показать примечательный результат: общая прибыль и доходность горизонта практически одинаковы. Инвестор с 7-летним горизонтом, в отличие от инвесторов с 4-летним или 10-летним горизонтом, достигает той же ставки доходности за период владения, независимо от того, снижаются ли, падают или остаются прежними процентные ставки.
Обратите внимание, что термины «доходность горизонта» (англ. 'horizon yield') и «ставка доходности за период владения» (англ. 'holding-period rate of return') используются здесь взаимозаменяемо. Иногда «доходность горизонта» относится к доходности облигаций, которые инвестору необходимо продать в конце периода владения.
|
Процентная ставка |
Будущая стоимость реинвестированного купона |
Цена продажи |
Общая доходность |
Доходность горизонта |
|---|---|---|---|---|
|
9.40% |
74.512177 |
96.481299 |
170.993476 |
10.408% |
|
10.40% |
76.835787 |
94.073336 |
170.909123 |
10.400% |
|
11.40% |
79.235183 |
91.748833 |
170.984016 |
10.407% |
Эта конкретная облигация была выбрана в качестве примера для демонстрации важного свойства дюрации Маколея: для конкретного предположения о волатильности доходности, дюрация Маколея указывает на инвестиционный горизонт, для которого риск реинвестирования купона и рыночная цена компенсируют друг друга.
В рассмотренном ранее примере дюрация Маколея для этой 10-летней 8% облигации составляет 7.0029 лет. Это одно из применений показателя дюрации, в котором «годы» имеют смысл, и в котором используют дюрацию Маколея, а не показатель модифицированной дюрации.
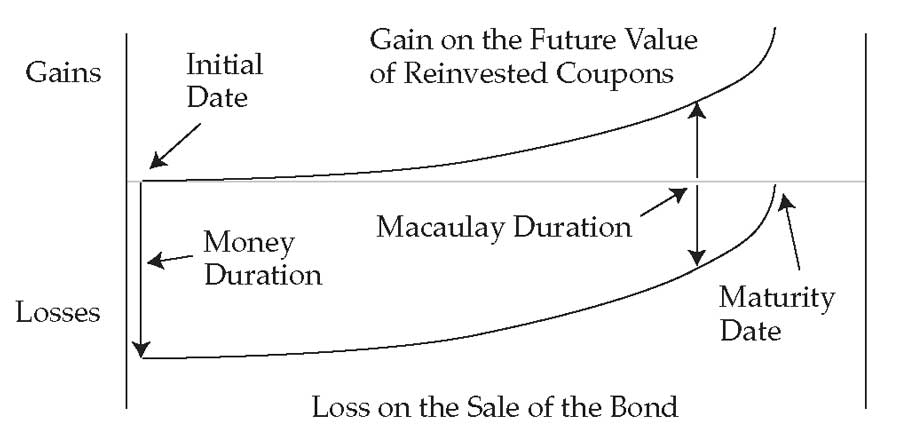
Предположение о волатильности доходности заключается в том, что существует единовременный «параллельный» сдвиг в кривой доходности, который происходит до наступления даты следующей выплаты купона. Иллюстрация 13 показывает это свойство дюрации облигации, используя допущение о том, что облигация первоначально оценивается по номинальной стоимости.
Иллюстрация 13. Риск процентных ставок, дюрация Маколея и инвестиционный горизонт.
Как показано на графике A в Иллюстрации 13, когда процентные ставки растут, дюрация оценивает немедленное падение стоимости. В частности, денежная дюрация указывает на изменение цены.
Затем, со временем, цена облигаций «стремится к номиналу».
Прибыль в будущей стоимости реинвестированных купонов в начале мала, но со временем увеличивается по мере получения большего количества купонов. Кривая указывает на дополнительную будущую стоимость реинвестированных купонов из-за более высокой процентной ставки.
В определенный момент эти два эффекта компенсируют друг друга, и прирост реинвестированных купонов становится равным убытку при продаже облигации. Этот момент времени является показателем дюрации Маколея.
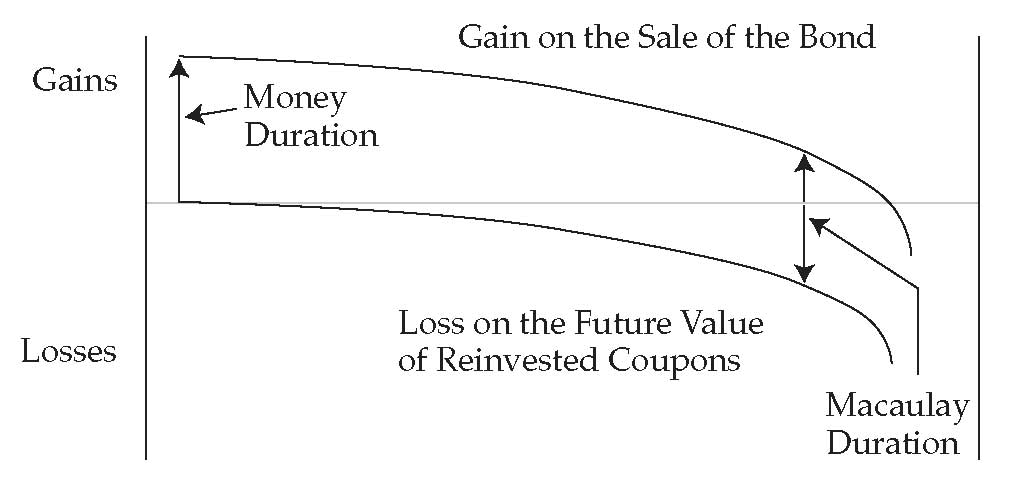
Та же ситуация показана на графике B, где процентные ставки снижаются, что приводит к снижению доходности облигаций и ставки реинвестирования купона. В цене облигации происходит немедленный скачок, оцениваемый денежной дюрацией, но затем эффект «стремления к номиналу» снижает цену с течением времени.
Влияние реинвестирования по более низкой ставке в начале невелико, но затем с течением времени становится более значительным. Убыток реинвестированных купонов связан с будущей стоимостью, если процентные ставки не снижаются.
Еще раз обратим внимание, что дюрация Маколея облигации указывает на момент времени, когда оба эффекта компенсируют друг друга, а прибыль от продажи облигации соответствует убытку от реинвестирования купонов.
Предыдущий численный пример и Иллюстрация 13 позволяют сделать следующие утверждения о взаимосвязи между риском процентных ставок, дюрацией Маколея и инвестиционным горизонтом.
- Когда инвестиционный горизонт больше, чем дюрация Маколея облигации, риск реинвестирования купона доминирует над риском рыночной цены. Риск инвестора заключается в низких процентных ставках.
- Когда инвестиционный горизонт равен дюрации Маколея, риск реинвестирования купона компенсирует рыночную цену.
- Когда инвестиционный горизонт меньше, чем дюрация Маколея облигации, риск рыночной цены доминирует над риском реинвестирования купонов. Риск инвестора заключается в высоких процентных ставках.
В этом числовом примере дюрация Маколея облигации составляет 7.0 лет. Утверждение 1 относится к инвестору с 10-летним горизонтом; Утверждение 2 - к инвестору с 7-летним горизонтом; а Утверждение 3 - к инвестору с 4-летним горизонтом.
Разница между дюрацией Маколея облигации и инвестиционным горизонтом называется разрывом дюрации. Разрыв дюрации (англ. 'duration gap') - это дюрация Маколея облигации за вычетом инвестиционного горизонта.
Инвестор с 10-летним горизонтом имеет отрицательный разрыв дюрации и в настоящее время подвергается риску более низких ставок.
Инвестор с 7-летним горизонтом имеет нулевой разрыв дюрации и в настоящее время подвергается риску процентных ставок.
Инвестор с 4-летним горизонтом имеет положительный разрыв дюрации и в настоящее время подвергается риску более высоких ставок.
Оговорка «в настоящее время» важна, потому что риск процентных ставок связан с немедленным изменением доходности к погашению облигации и ставок реинвестирования купона. Со временем инвестиционный горизонт уменьшается, а дюрация Маколея также меняется. Следовательно, разрыв дюрации также меняется.
Пример (16) расчета дюрации Маколея.
Инвестор планирует уйти в отставку через 10 лет. В рамках пенсионного портфеля инвестор покупает недавно выпущенную 12-летнюю облигацию с 8% годовым купоном.
Облигация приобретается по номинальной стоимости, поэтому ее доходность к погашению составляет 8.00%, что соответствует эффективной годовой ставке.
- Рассчитайте приблизительную дюрацию Маколея для облигации, используя увеличение и снижение доходности к погашению на 1 б.п. При расчете цен используйте округление до шести знаков.
- Рассчитайте разрыв дюрации на момент покупки.
- Связана ли покупка этой облигации с риском более высоких или более низких процентных ставок? Риск процентных ставок здесь означает немедленный, единовременный, параллельный сдвиг кривой доходности.
Решение для части 1:
Приблизительная модифицированная дюрация облигации составляет 7.5361.
\( PV_0 \) = 100, \( PV_+ \) = 99.924678 и \( PV_- \) = 100.075400.
\( \dst PV_+ = {8 \over (1.0801)^1 } + \ldots + {108 \over (1.0801)^{12} } = 99.924678 \)
\( \dst PV_+ = {8 \over (1.0799)^1 } + \ldots + {108 \over (1.0799)^{12} } = 100.075400 \)
ApproxModDur = \( \dst { 100.075400 - 99.924678 \over 2 \times 0.0001 \times 100} = 7.5361 \)
Приблизительная дюрация Маколея составляет 8.1390 (= 7.5361 \(\times\) 1.08).
Решение для части 2:
При инвестиционном горизонте 10 лет, разрыв дюрации при покупке этой облигации будет отрицательным: 8.1390 - 10 = -1.8610.
Решение для части 3:
Отрицательный разрыв дюрации влечет за собой риск более низких процентных ставок. Если точнее, риск представляет собой немедленный, единовременный, параллельный, направленный вниз сдвиг кривой доходности, поскольку риск реинвестирования купонов доминирует над риском рыночной цены.
Убыток от реинвестирования купонов по ставке ниже 8% больше, чем прибыль от продажи облигации по цене выше траектории цены постоянной доходности.