CFA - Показатель выпуклости облигации

Модифицированная дюрация оценивает первичное влияние на процентное изменение цены облигации, с учетом изменения доходности к погашению. Вторичное влияние оценивается с помощью показателя выпуклости, который показан в Иллюстрации 10 для обыкновенной (без опционов) облигации с фиксированной ставкой.

Иллюстрация 10. Выпуклость обыкновенной (без опционов) облигации с фиксированной ставкой.

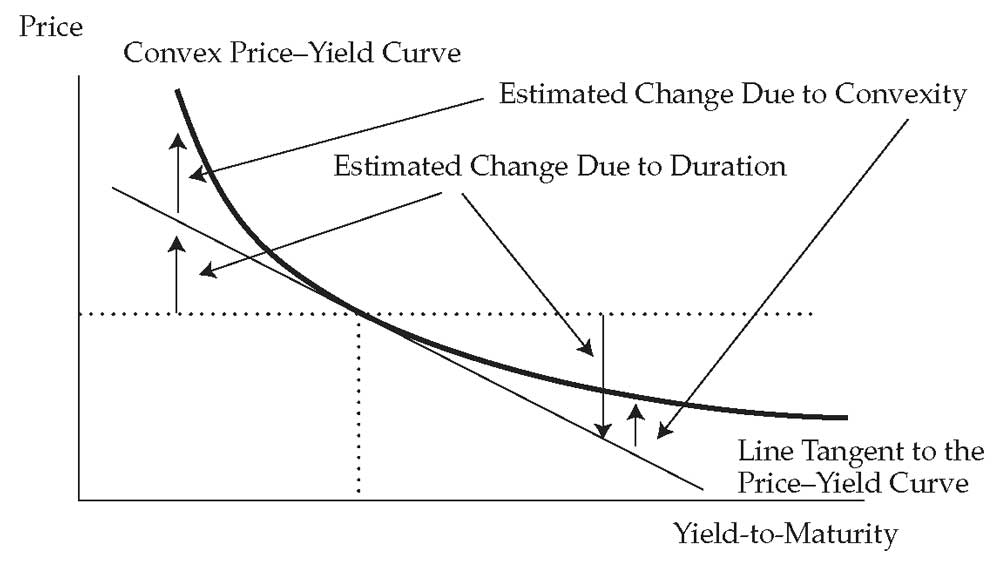
Выпуклость обыкновенной (без опционов) облигации с фиксированной ставкой.

Взаимосвязь между ценой облигаций и доходностью к погашению - это изогнутая (выпуклая) линия, показанная в Иллюстрации 10. Эта изогнутая линия показывает фактическую цену облигации, с учетом ее рыночной ставки дисконтирования.

Дюрация (в частности, денежная дюрация) оценивает изменение цены облигации вдоль прямой линии, которая касается изогнутой кривой. Для незначительных изменений доходности к погашению разница между линиями небольшая. Но для больших изменений разница становится значительной.

Показатель выпуклости облигации используется для улучшения оценки процентного изменения цены, полученной только за счет модифицированной дюрации. Формула 13 представляет собой оценку процентного изменения полной цены облигации с поправкой на выпуклость.

\( \begin{aligned} \dst
\% \Delta \PV^{Full} &\approx
\left( -{\rm AnnModDur} \times \Delta {\rm Yield} \right) \\
&+ \left[ {1 \over 2} \times {\rm AnnConvexity} \times (\Delta {\rm Yield})^2 \right]
\end{aligned} \) (Формула 13)

Первое выражение в скобках, эффект «первого порядка», совпадает с Формулой 6. Годовая модифицированная дюрация, AnnModDur, умножается на изменение годовой доходности к погашению, \(\Delta Yield\). Второе выражение в скобках, эффект «второго порядка», является поправкой на выпуклость.

Поправка на выпуклость (англ. 'convexity adjustment') - это годовой показатель выпуклости, AnnConvexity, умноженный на 1/2 и на изменение доходности к погашению в квадрате. Эта дополнительная поправка является положительной суммой, увеличивающей или снижающей доходность.

В Иллюстрации 10 эта сумма прибавляется к линейной оценке дюрации, что дает скорректированную оценку, очень близкую к фактической цене на кривой. Но это все еще приблизительная оценка, поэтому в формуле используется знак \(\approx\).

Подобно дюрации Маколея и модифицированной дюрации, годовой показатель выпуклости можно рассчитать несколькими способами. Его можно рассчитать с использованием таблиц, таких как в Иллюстрациях 2 и 3.

Также можно получить формулу в закрытой форме с использованием вычислений и алгебры.

Пошаговое получение этой формулы приведено в книге Donald J. Smith, Bond Math: The Theory behind the Formulas, 2nd edition (Hoboken, NJ: John Wiley & Sons, 2014).

Но, как и модифицированную дюрацию, показатель выпуклости можно получить приближенно с определенной точностью. Формула 14 позволяет получить приблизительную оценку показателя выпуклости, ApproxCon.

\( \dst {\rm ApproxCon} =
{\PV_- + \PV_+ - 2 \times PV_0 \over (\Delta {\rm Yield})^2 \times \PV_0} \) (Формула 14)

Эта формула использует те же исходные данные, что и Формула 7 для расчета ApproxModDur. Новая цена при увеличении доходности к погашению обозначается как \(\PV_+\). Новая цена при уменьшении доходности к погашению обозначается как \(\PV_-\).

Первоначальная цена обозначается как \(\PV_0\). Это полные цены, включающие начисленные проценты.

Точность этого приближения можно продемонстрировать с помощью особого примера бескупонной облигации. Отсутствие купонных платежей упрощает показатели риска процентной ставки.

Дюрация Маколея для бескупонной облигации, выраженная в периодах погашения, равна \( N - t/T \). Точный показатель выпуклости бескупонной облигации, также выраженный в периодах, рассчитывается с помощью Формулы 15.

\( \dst {\rm Convexity} = {(N - t/T) \times (N + 1 - t/T) \over (1+r)^2} \) (Формула 15)

\(N\) - это количество периодов до погашения с начала текущего периода, \(t/T\) - это прошедшая доля периода, а \(r\) - доходность к погашению за период.

В качестве примера этого расчета рассмотрим долгосрочную бескупонную казначейскую облигацию США. Страница YAS Bloomberg приведена в Иллюстрации 11.

Иллюстрация 11. Страница YAS Bloomberg для бескупонной казначейской облигации США.

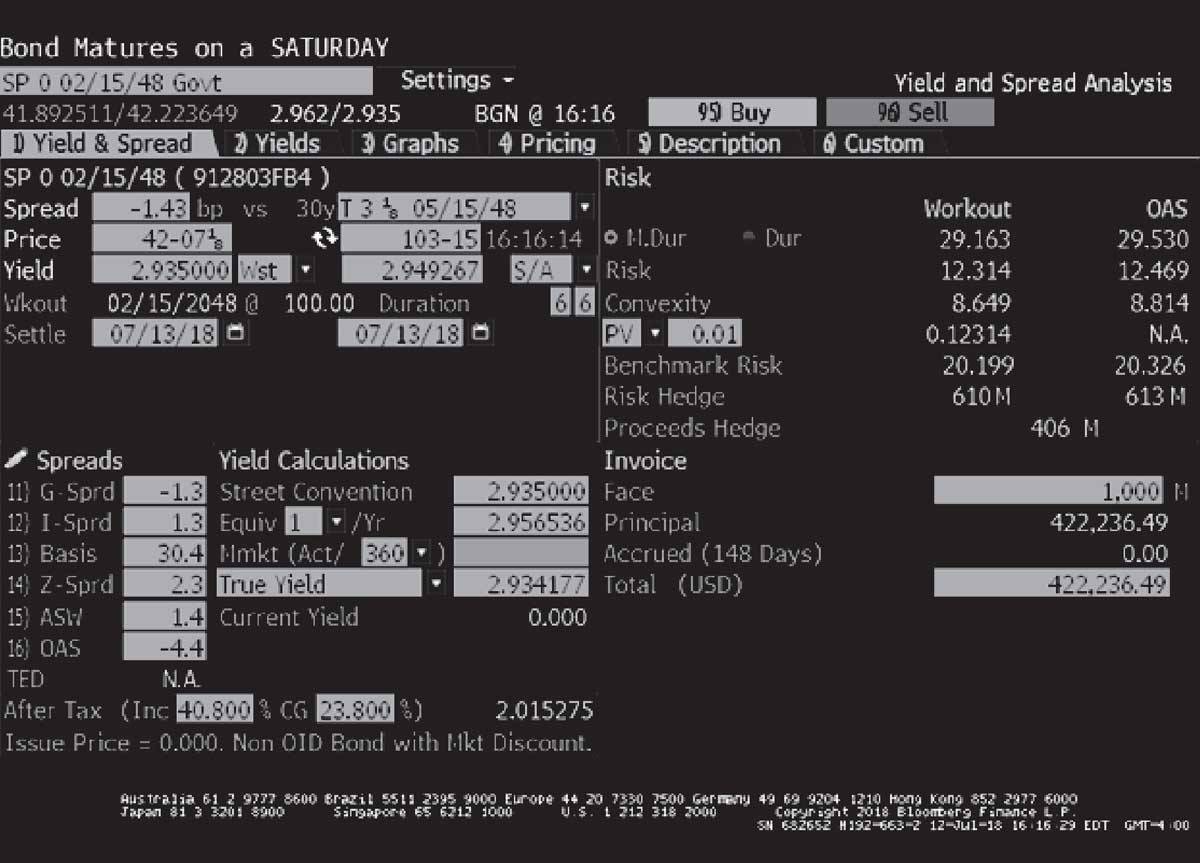
Страница YAS Bloomberg для бескупонной казначейской облигации США.

Облигация погашается 15 февраля 2048 года, и ее заявленная цена составила 42.223649 на 100 д.е. номинальной стоимости при расчете на 13 июля 2018 года. Ее доходность к погашению составила 2.935% при полугодовом начислении купона.

Несмотря на то, что это бескупонная облигация, ее доходность к погашению основана подсчете дней по соглашению фактические/фактические дни. Дата расчета приходится на 148 день в 181-дневном периоде. Годовая модифицированная дюрация составляет 29.163.

Для этой облигации \(N\) = 60, \(t/T\) = 148/181 и \(r\) = 0.02935/2. Если подставить эти переменные в Формулу 15, расчет дает выпуклость 3,459.45 в полугодовом исчислении.

\( \dst { \left[ 60 - 148/181 \right] \times \left[ 60+1-148/181 \right]
\over \dst \left( 1+ {0.02935 \over 2} \right)^2} = 3,459.45 \)

Как и в случае с другими показателями дюрации, выпуклость приводится в годовом исчислении на практике, а также для использования в качестве поправки выпуклости в Формуле 13.

Доходность к погашению по этой бескупонной облигации указана в полугодовом исчислении, что означает периодичность 2. Следовательно, годовой показатель выпуклости составляет 864.9.

\( \dst {3,459.45 \over 4} = 864.9 \)

Например, предположим, что доходность к погашению предположительно снизится на 10 б.п., с 2.935% до 2.835%. При годовой модифицированной дюрации 29.163 и годовой выпуклости 864.9, ожидаемое процентное увеличение цены составляет 2.9595%.

\( \begin{aligned}
\%\Delta \PV^{Full} &\approx
[-29.163 \times -0.0010] + {1\over 2} \times 864.9 \times (-0.0010)^2 \\[1ex]
&= 0.029163 + 0.000432 \\
&= 0.029595
\end{aligned} \)

Модифицированная дюрация без учета поправки дает прирост цены 2.9163%. Поправка выпуклости добавляет к результату 4.32 б.п.

Долгосрочная бескупонная облигация в Иллюстрации 11 показывает разницу между дюрацией доходности и выпуклостью и дюрацией кривой и выпуклостью, даже для облигации без опционов. Ее модифицированная дюрация составляет 29.163, тогда как ее эффективная дюрация составляет 29.530.

Ее выпуклость доходности, представленная на странице YAS Bloomberg, составляет 8.649, а ее эффективная выпуклость составляет 8.814 (Обратите внимание, что Bloomberg масштабирует показатель выпуклости путем деления его на 100).

В целом, различия усиливаются, когда кривая базовой доходности не является плоской, когда облигация имеет длительный оставшийся срок погашения, а облигация оценивается со значительным дисконтом или премией.

Чтобы найти ApproxCon для этой долгосрочной бескупонной облигации, рассчитаем \(\PV_0\), \(\PV_+\) и \(\PV_-\), что дает значения доходности 2.935%, 2.945% и 2.925%соответственно. В этом примере \( \Delta {\rm Yield} = 0.0001.

Используя эти результаты, сначала рассчитайте ApproxModDur, используя Формулу 7, чтобы подтвердить, что эти расчетные данные верны. В Иллюстрации 11 модифицированная дюрация составляет 29.163.

\( \dst
{\rm ApproxModDur} = {42.346969-42.100694 \over 2 \times 0.0001 \times 42.223649} = 29.163 \)

При расчете с использованием Формулы 14, ApproxCon составляет 864.9.

\( \dst
{\rm ApproxCon} = {42.346969+42.100694- (2\times 42.223649) \over 0.0001^2 \times 42.223649} = 864.9 \)

Этот результат, 864.9, является приближенным значением выпуклости в годовом выражении. Количество периодов в году включено в расчет цен.

Полученный приближенный результат в этом примере такой же, как и «точный» результат, полученный с использованием формулы в закрытой форме, применяемой для бескупонных облигаций. Небольшая разница вряд ли будет иметь значение для практического применения.

Поскольку это отдельная бескупонная облигация, для нее легко рассчитать новую цену, если доходность к погашению снижается на 50 б.п., до 2.435%.

\( \dst
{100 \over \dst \left(1+{0.02435 \over 2} \right)^{60}} \times
\left(1+{0.02435 \over 2} \right)^{148/181} = 48.860850 \)

Следовательно, фактическое процентное увеличение цены составляет 15.7192%.

\( \dst {48.860850 - 42.223649 \over 42.223649 } = 0.157192 \)

Оценка с поправкой на выпуклость составляет 15.6626%.

\( \begin{aligned}
\%\Delta \PV^{Full} &\approx
[-29.163 \times -0.0050] + {1\over 2} \times 864.9 \times (-0.0050)^2 \\[1ex]
&= 0.145815 + 0.010811 \\
&= 0.156626
\end{aligned} \)

Пример 13.

Итальянский банк открывает большую позицию в корпоративной облигации с 7.25% годовым купоном, которая погашается 4 апреля 2034 года. Доходность к погашению облигации составляет 7.44% при расчете на 27 июня 2019 года, что соответствует ее заявленной эффективной годовой ставке.

Эта дата расчета приходится на 83 день в 360-дневном году, при использовании для подсчета дней метода 30/360 дней.

1. Рассчитайте полную цену облигации на 100 д.е. номинальной стоимости.
2. Рассчитайте приблизительную модифицированную дюрацию и приблизительную выпуклость, используя увеличение и уменьшение доходности к погашению на 1 б.п.
3. Рассчитайте процентное изменение цены с поправкой на выпуклость, возникающее в результате увеличения доходности к погашению на 100 б.п.
4. Сравните рассчитанное процентное изменение цены с фактическим изменением, предполагая, что доходность к погашению увеличится до 8.44% на эту дату расчета.

---

Решение:

Промежуток времени с начала текущего периода 4 апреля 2019 года до наступления срока погашения 4 апреля 2034 составляет 15 лет.

1. Полная цена облигации составляет 99.956780 на 100 д.е. номинальной стоимости.

\( \begin{aligned} \dst
\PV_0 &= \left[ {7.25 \over 1.0744^1} + \ldots + {107.25 \over 1.0744^{15}} \right]
\times 1.0744^{83/360} = 99.956780
\end{aligned} \)

2. \(\PV_+\) = 99.869964 и \(\PV_-\) = 100.043703.

Приблизительная модифицированная дюрация составляет 8.6907.

\( \dst
{\rm ApproxModDur} = {100.043703 + 99.869964 \over 2 \times 0.0001 \times 99.956780} = 8.6907 \)

Приблизительная выпуклость составляет 107.157.

\( \dst
{\rm ApproxCon} = {100.043703 + 99.869964 - (2 \times 99.956780) \over
0.0001^2 \times 99.956780} = 107.157 \)

3. Процентное снижение цены с поправкой на выпуклость в результате увеличения доходности на 100 б.п. оценивается в 8.1555%. Модифицированная дюрация без учета поправки оценивает процентное снижение до 8.6907%. Поправка на выпуклость добавляет к результату 53.52 б.п.

\( \begin{aligned}
\%\Delta \PV^{Full} &\approx
[-8.6907 \times -0.0100] + {1\over 2} \times 107.157 \times (-0.0100)^2 \\[1ex]
&= -0.086907 + 0.005358 \\
&= -0.81549
\end{aligned} \)

4. При снижении доходности к погашению с 7.44% до 8.44% новая полная цена на эту дату расчета составляет 91.780921.

Фактическое процентное изменение цены облигации составляет -8.1794%. Оценка с поправкой на выпуклость составляет -8.1549%, тогда как изменение цены без поправки составляет -8.6907%.

---

Денежная дюрация облигации отражает эффект первого порядка на полную цену облигации в валюте облигации, с учетом изменения доходности к погашению.

Показатель денежной выпуклости (MoneyCon, 'money convexity') является эффектом второго порядка. Денежная выпуклость облигации - это годовая выпуклость, умноженная на полную цену:

\( \begin{aligned} \dst
\Delta \PV^{Full} &\approx -({\rm MoneyDur} \times \Delta {\rm Yield}) \\[1ex]
&+ \left[ {1 \over 2} \times {\rm MoneyCon} \times (\Delta {\rm Yield})^2 \right]
\end{aligned} \) (Формула 16)

В качестве примера денежной выпуклости, рассмотрим еще раз страховую компанию из Гонконга, которая удерживает позицию в размере HKD100,000,000 в 6.00% облигации, которая погашается 14 февраля 2027 года.

В исходном примере, при использовании денежной дюрации убыток цены составляет HKD6,184,418, если доходность к погашению увеличивается на 100 б.п.

Денежная дюрация для этой позиции составляет  HKD618,441,784. Эту оценку можно улучшить путем включения в расчет поправки на выпуклость. Исходные данные для расчета приблизительной модифицированной дюрации 6.1268 при изменении доходности к погашению на 5 б.п. (\(\Delta\) Yield = 0.0005):

\(\PV_0\) = 100.940423, \(\PV_+\) = 100.631781 и \(\PV_-\) = 101.250227.

Подставим эти значения в Формулу 14, чтобы рассчитать приблизительную выпуклость.

Денежная выпуклость равна 46.047, умноженным на рыночную стоимость этой позиции, HKD100,940,423. Убыток с поправкой на выпуклость с учетом роста доходности к погашению на 100 б.п. составляет HKD5,952,018.

\( \begin{aligned} \dst
&-[6.1268 \times 100,940,423 \times 0.0100] + \\[1ex]
&\left[ {1 \over 2} \times 46.047 \times 100,940,423 \times (0.0100)^2 \right] + \\[1ex]
&= -6,184,418 + 232,400 \\[1ex]
&= -5,952,018
\end{aligned} \)

Факторы, которые приводят к большей выпуклости, такие же, как и для дюрации. Облигация с фиксированной ставкой с более длительным оставшимся сроком погашения, более низкой ставкой купона и более низкой доходностью к погашению имеет большую выпуклость, чем облигация с более коротким оставшимся сроком погашения, более высокой ставкой купона и более высокой доходностью к погашению.

Другим фактором является дисперсия (рассеивание) денежных потоков, т.е. степень, в которой платежи распределены во времени.

Если две облигации имеют одинаковую дюрацию, то, та, что имеет большую дисперсию денежных потоков, имеет большую выпуклость. Положительные атрибуты большей выпуклости для инвестора показаны в Иллюстрации 12.

Иллюстрация 12. Положительные атрибуты большей выпуклости облигации для традиционной облигации (без опционов).

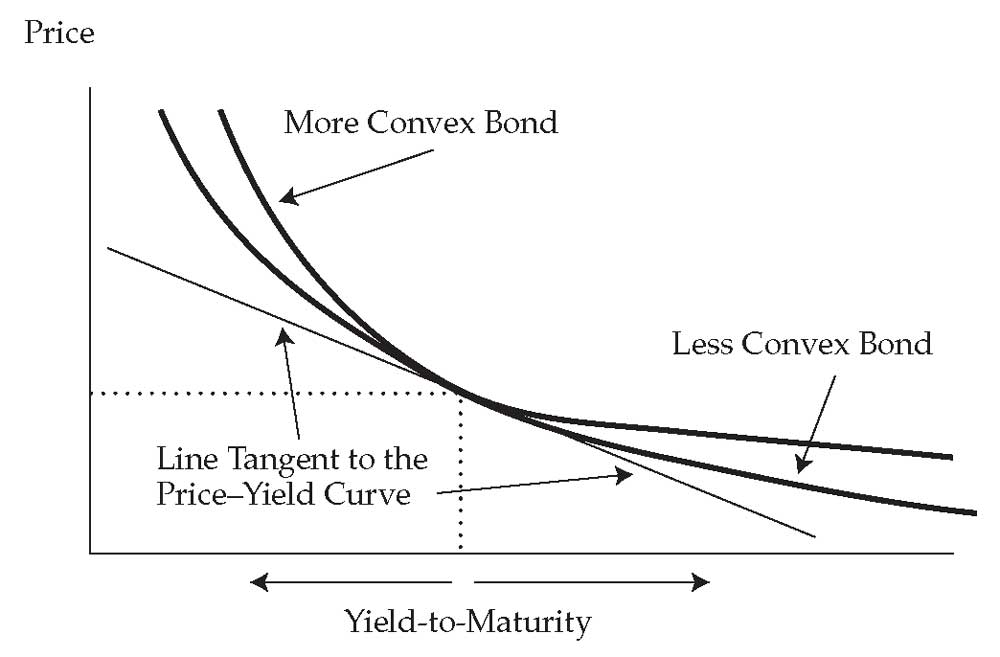
Положительные атрибуты большей выпуклости облигации для традиционной облигации (без опционов).

Предполагается, что две облигации в Иллюстрации 12 имеют одинаковую цену, доходность к погашению и модифицированную дюрацию. Следовательно, они делят между собой общую прямую, касающуюся их кривых цены-доходности. Преимущество большей выпуклости возникает при изменении их доходности к погашению.

При одинаковом снижении доходности к погашению, более выпуклая облигация будет оцениваться по большей цене. И при одинаковом увеличении доходности к погашению, более выпуклая облигация меньше потеряет в цене.

Вывод заключается в том, что более выпуклая облигация превосходит менее выпуклую облигацию как на бычьих рынках (растущая цена), так и на медвежьих рынках (падающая цена).

Этот вывод предполагает, однако, что этот положительный атрибут не включается в цену облигации. В той степени, в которой он включается в цену, более выпуклая облигация будет иметь более высокую цену (и более низкую доходность к погашению).

Это не уменьшает важность выпуклости. Это только предполагает, что инвестор должен заплатить за это. Как говорят экономисты, «бесплатных обедов не бывает».

Пример (14) расчета модифицированной дюрации.

Инвестиционный менеджер британской пенсионной программы рассматривает две облигации, которые должна выпустить крупная страховая компания.

Первая - это 30-летняя облигация с 4% полугодовым купоном. Вторая - 100-летняя 4% облигация с полугодовым купоном. Ожидается, что обе облигации будут продаваться по номинальной стоимости при выпуске.

Рассчитайте приблизительную модифицированную дюрацию и приблизительную выпуклость для каждой облигации при увеличении и снижении годовой доходности к погашению на 5 б.п. Точность результата должна составить до шести знаков после запятой на 100 д.е. номинальной стоимости.

---

Решение:

В этом расчете доходность за полугодовой период увеличивается на 2.5 б.п. до 2.025% и снижается на 2.5 б.п. до 1.975%. 30-летняя облигация имеет приблизительную модифицированную дюрацию 17.381 и приблизительную выпуклость 420.80.

100-летняя облигация имеет приблизительную модифицированную дюрацию 24.527 и приблизительную выпуклость 1,132.88.

100-летняя облигация предлагает более высокую модифицированную дюрацию - 24.527 по сравнению с 17.381, и гораздо больший уровень выпуклости - 1,132.88 по сравнению с 420,80.

---

Точно так же, как первичный эффект или эффект первой степени, эффект сдвига кривой базовой доходности оценивается эффективной дюрацией. Вторичный эффект или эффект второго порядка оценивается эффективной выпуклостью.

Эффективная выпуклость облигации является показателем выпуклости кривой, который оценивает вторичный эффект изменения кривой базовой доходности. Модель ценообразования используется для определения новых цен, когда кривая базовой доходности смещается вверх (\(\PV_+\)) и вниз (\(\PV_-\)) на то же самое значение (\(\Delta {\rm Curve}\)).

Эти изменения несут в себе другие постоянные факторы, например, кредитный спред. Формула 17 используется для расчета эффективной выпуклости (EffCon, effective convexity) с учетом первоначальной цены (\(\PV_0\)).

\( \dst {\rm EffCon} =
{ \PV_- + \PV_+ - 2 \times \PV_0  \over  (\Delta {\rm Curve})^2 \times \PV_0 } \) (Формула 17)

Эта формула очень похоже на Формулу 14 для расчета приблизительной выпуклости доходности. Разница заключается в том, что в Формуле 14 знаменатель включает в себя изменение доходности к погашению в квадрате, \( (\Delta {\rm Yield})^2 \).

Здесь знаменатель включает в себя изменение кривой базовой доходности в квадрате \( (\Delta {\rm Curve})^2 \).

Рассмотрим еще раз пример отзывной облигации из раздела про эффективную дюрацию. Предполагается, что модель ценообразования опционов используется для генерации цен на эти отзывные облигации:

\(\PV_0\) = 101.060489, \(\PV_+\) = 99.050120, \(\PV_-\) = 102.890738 и \( \Delta {\rm Curve} \) = 0.0025.

Эффективная дюрация для этой отзывной облигации составляет 7.6006.

EffDur = \( \dst {102.890738-99.050120 \over 2 \times 0.0025 \times 101.060489} = 7.6006 \)

Если подставить эти данные в Формулу 17, эффективная выпуклость составит -285.17.

Отрицательная выпуклость, которую можно назвать «вогнутостью», является важной особенностью отзывных облигаций. Облигации с пут-опционом, с другой стороны, всегда имеют положительную выпуклость. Как эффект второго порядка, эффективная выпуклость указывает на изменение в эффекте первого порядка (т.е. эффективной дюрации) при изменении кривой базовой доходности.

В Иллюстрации 8, при снижении базовой доходности, наклон линии, касающейся кривой безотзывной облигации, становится более крутым, что указывает на положительную выпуклость. Но наклон линии, касающейся кривой отзывной облигации, становится более плоским, когда базовая доходность снижается.

Технически, кривая достигает точки перегиба, когда эффективная выпуклость смещается от положительного к отрицательному диапазону.

Таким образом, когда эта базовая доходность высокая, а сумма встроенного колл-опциона низкая, отзывные и безотзывные облигации испытывают очень схожие эффекты от изменения процентных ставок. Они имеют положительную выпуклость.

Но по мере уменьшения базовой доходности, кривые расходятся. В определенный момент отзывная облигация переходит в диапазон отрицательной выпуклости, что указывает на то, что встроенный колл-опцион имеет большую ценность для эмитента и будет с большей вероятностью использоваться.

Эта ситуация ограничивает потенциальное повышение цен на облигацию в результате более низких процентных ставок, будь то из-за более низкой базовой доходности или более низкого кредитного спреда.

Другой способ понять, почему отзывная облигация может иметь отрицательную выпуклость, заключается в преобразовании Формулы 17.

\( \dst {\rm EffCon} =
{ \left[ \PV_- - \PV_0 \right] -  \left[ \PV_0 - \PV_+ \right]  \over
(\Delta {\rm Curve})^2 \times \PV_0 } \)

В числителе первое выражение в скобках является увеличением цены при снижении кривой базовой доходности. Второе выражение в скобках - это снижение цены при повышении кривой базовой доходности. Для безотзывной облигации увеличение всегда больше, чем уменьшение (в абсолютном выражении).

Этот результат является «эффектом выпуклости» для взаимосвязи между ценой облигации и доходностью к погашению. Для отзывной облигации увеличение может быть меньше, чем уменьшение (в абсолютном выражении). Это создает отрицательную выпуклость, как показано в Иллюстрации 8.