CFA - Источники доходности ценных бумаг с фиксированным доходом
Рассмотрим источники формирования прибыли ценных бумаг с фиксированным доходом, а также влияние процентных ставок и сроков владения на ставку доходности и примеры этого влияния, - в рамках изучения ценных бумаг с фиксированным доходом по программе CFA.
Финансовым аналитикам важно хорошо понимать характеристики риска и доходности инвестиций в ценные бумаги с фиксированным доходом.
Многие финансовые активы и обязательства с известными будущими денежными потоками можно оценивать с использованием тех же принципов, которые применяются при оценке облигаций с фиксированной ставкой, обращающихся на мировом рынке.
Отправной точкой для этого анализа является доходность к погашению или внутренняя норма доходности по будущим денежным потокам, которая описана в чтении об оценке фиксированного дохода.
На доходность облигации с фиксированной ставкой влияют многие факторы, и наиболее важным из них является получение процентных и основных платежей в полной сумме и в запланированные сроки.
При допущении об отсутствии дефолта, на доходность также воздействует изменение процентных ставок, которое повлияет на реинвестирование купона и цену облигации, если она будет продана до наступления срока погашения. Два показателя изменения цены можно вывести из математической зависимости, используемой для расчета цены облигации:
- Дюрация или средний срок погашения (англ. 'duration') - оценивает изменение цены на данное изменение процентных ставок.
- Выпуклость (англ. 'convexity') - улучшает оценку показателя дюрации, принимая во внимание тот факт, что зависимость между ценой и доходностью облигации с фиксированной ставкой не является линейной.
В целом, инвестор в облигации с фиксированной ставкой имеет три источника прибыли:
- получение обещанных купонных и основных платежей в запланированные даты,
- реинвестирование купонных платежей и
- потенциальный прирост или убыток капитала при продаже облигации до наступления срока погашения.
В этом обсуждении мы допускаем, что эмитент производит купонные и основные платежи в соответствии с запланированным графиком. Мы фокусируемся в первую очередь на риске процентных ставок (т.е. риске изменения процентных ставок), который влияет на реинвестирование купонных платежей и рыночную цену при продаже облигации до наступления срока погашения.
Кредитный риск рассматривается в следующих разделах этого чтения и является главной темой чтения «Основы кредитного анализа».
Когда облигация приобретается с премией или дисконтом, это добавляет еще один фактор к ставке доходности.
Напомним, что дисконтная облигация предлагает инвестору «недостаточную» купонную ставку, то есть ставку ниже рыночной ставки дисконтирования.
Амортизация дисконта в каждом периоде обеспечивает доходность в соответствии с рыночной ставкой дисконтирования, при этом балансовая стоимость облигации постепенно «подтягивается к номиналу».
Для облигации с премией купонная ставка превышает рыночную ставку дисконтирования, а амортизация премии корректирует доходность в соответствии с рыночной ставкой дисконтирования. Благодаря амортизации балансовая стоимость облигации достигает номинальной стоимости при погашении.
На нескольких примерах мы продемонстрируем влияние изменения процентных ставок на реализованные ставки доходности двух инвесторов. В данном случае, процентные ставки - это ставки, по которым реинвестируются купонные платежи, а также рыночные ставки дисконтирования на момент покупки и на момент продажи, если облигация не будет удерживаться до погашения.
В Примерах 1 и 2 процентные ставки не меняются. Однако два инвестора имеют разные временные горизонты для удержания облигаций. Примеры 3 и 4 показывают воздействие увеличения процентных ставок на общую прибыль двух инвесторов.
Примеры 5 и 6 показывают влияние снижения процентных ставок. В каждом из шести примеров инвестор первоначально покупает 10-летнюю облигация с 8% годовым купоном по цене 85.503075 на 100 д.е. номинальной стоимости. Доходность к погашению облигации составляет 10.40%.
85.503075 &= {8 \over (1+r)^1} + {8 \over (1+r)^2} + {8 \over (1+r)^3} + {8 \over (1+r)^4} + {8 \over (1+r)^5} \\
&+ {8 \over (1+r)^6} + {8 \over (1+r)^7} + {8 \over (1+r)^8} + {8 \over (1+r)^9} + {108 \over (1+r)^{10}}, \\[1ex]
&r = 0.1040
\end{aligned} \)
Пример (1) расчета дохода инвестора по облигации.
Долгосрочный инвестор приобретает 10-летнюю 8% облигацию с годовым купоном за 85.503075 д.е. на 100 д.е. номинальной стоимости и удерживает ее до погашения. Инвестор получает серию из 10 купонных платежей в размере 8 (на 100 номинальной стоимости) на общую сумму 80, плюс выплату основной суммы (100) при погашении.
Помимо получения купона и основной суммы, инвестор имеет возможность реинвестировать денежные потоки. Если купонные платежи будут реинвестированы по ставке 10.40%, будущая стоимость купонов на дату погашения облигации составит 129.970678 на 100 номинальной стоимости.
&8 \times 1.1040^9 + 8 \times 1.1040^8 + 8 \times 1.1040^7 + 8 \times 1.1040^6 + \\
&8 \times 1.1040^5 + 8 \times 1.1040^4 + 8 \times 1.1040^3 + 8 \times 1.1040^2 + \\
&8 \times 1.1040^1 + 8 = 129.970678
\end{aligned} \)
Первый купон на сумму 8 реинвестируется по ставке 10.40% в течение 9 лет до погашения, второй реинвестируется в течение 8 лет и так далее.
Будущую стоимость аннуитета можно легко рассчитать в экселе или с помощью финансового калькулятора, используя 8 для платежа, получаемого в конце каждого из 10 периодов.
Сумма, превышающая купоны, 49.970678 (= 129.970678 - 80), является прибылью от «процентов с процентов» в результате сложного начисления процентов.
Общая прибыль инвестора составляет 229.970678 и равна сумме реинвестированных купонов (129.970678) и основной сумме при погашении (100). Реализованная ставка доходности составляет 10.40%.
\( \dst
85.503075 = {229.970678 \over (1+r)^10}, r = 0.1040
\)
Пример 1 демонстрирует, что доходность к погашению на момент покупки облигаций оценивает ставку доходности инвестора с учетом трех допущений:
- инвестор удерживает облигацию до погашения,
- эмитент не допускает дефолт, и
- процентные купонные платежи реинвестируются по той же процентной ставке.
Пример 2 рассматривает другого инвестора, который покупает 10-летнюю 8% облигацию с годовым купоном и платит за нее ту же цену.
Однако, этот инвестор имеет 4-летний инвестиционный горизонт. Поэтому купоны реинвестируются только в течение 4 лет, и облигация продается сразу после получения четвертого купона.
Пример (2) расчета дохода инвестора по облигации.
Второй инвестор покупает 10-летнюю облигацию с годовым купоном 8% и продает ее через 4 года. Если предположить, что купонные платежи будут реинвестированы по ставке 10.40% в течение четырех лет, будущая стоимость реинвестированных купонов составит 37.347111 на 100 номинальной стоимости.
8 \times 1.1040^3 + 8 \times 1.1040^2 + 8 \times 1.1040^1 + 8 = 37.347111
\end{aligned} \)
Прибыль от начисления процентов на проценты составляет 5.347111 (= 37.347111 - 32). Через 4 года, когда облигация будет продана, у нее останется 6 лет до погашения. Если доходность к погашению останется на уровне 10.40%, цена продажи облигации составит 89.668770.
\( \begin{aligned} \dst
&{8 \over 1.1040^1}+ {8 \over 1.1040^2}+ {8 \over 1.1040^3}+ {8 \over 1.1040^4}+ \\
&{8 \over 1.1040^5}+ {108 \over 1.1040^6} = 89.668770
\end{aligned} \)
Общий доход составляет 127.015881 (= 37.347111 + 89.668770), а реализованная ставка доходности составляет 10.40%.
\( \begin{aligned} \dst
85.503075 = {127.015881 \over (1+r)^4}, \ \ r = 0.1040
\end{aligned} \)
В Примере 2 доходность инвестиционного горизонта инвестора составляет 10.40%.
Доходность горизонта (англ. 'horizon yield') - это внутренняя ставка доходности, которая соответствует разнице между общим доходом (сумма реинвестированных купонных платежей и цены продажи или суммы погашения) и ценой покупки облигации.
Доходность горизонта при инвестициях в облигации - это годовая ставка доходности за период владения облигациями.
Пример 2 демонстрирует, что реализованная доходность горизонта соответствует исходной доходности к погашению, если:
- купонные платежи реинвестируются по той же процентной ставке, что и исходная доходность к погашению, и
- облигация продается по цене, соответствующей траектории цен постоянной доходности, что подразумевает, что инвестор не получает прироста или убытка капитала при продаже облигации.
Прироста капитала возникает, если облигация продается по цене выше траектории цен постоянной доходности, а убыток капитала возникает, если облигация продается по цене ниже траектории цен постоянной доходности.
Эта траектория основана на доходности к погашению при покупке облигации. В Иллюстрации показана траектория для 10-летней облигации с годовым купоном 8%, приобретенной по цене 85.503075 на 100 д.е. номинальной стоимости.
Иллюстрация 1. Траектория цен постоянной доходности для 10-летней облигации с годовым купоном 8%.
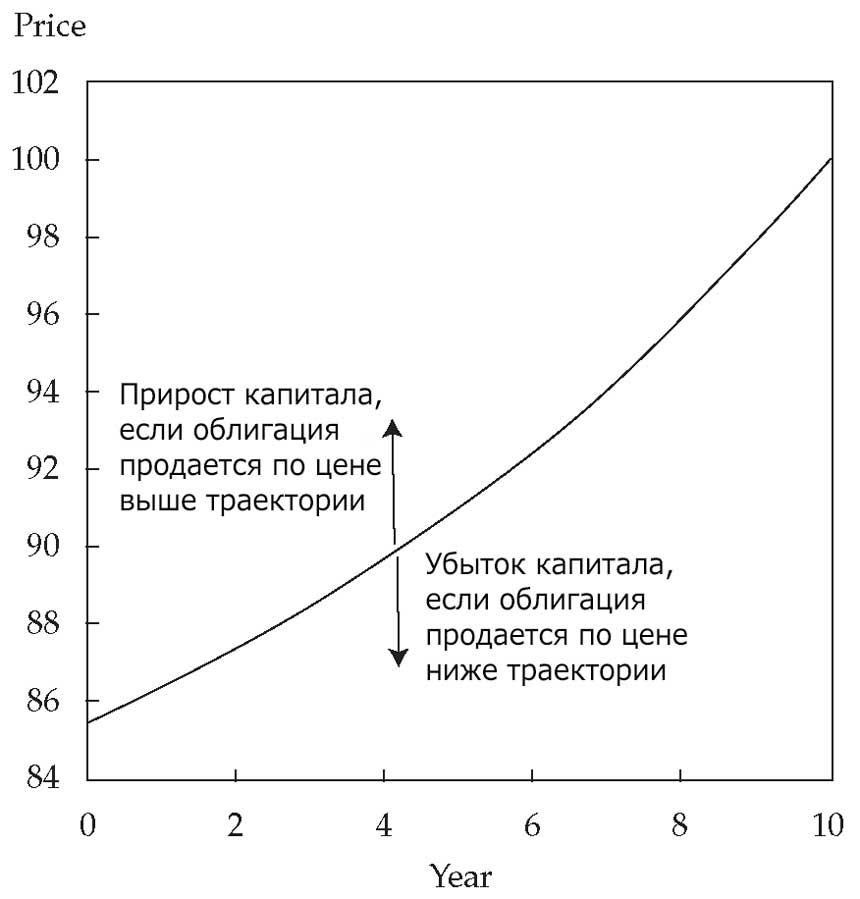
Траектория цен постоянной доходности для 10-летней облигации с годовым купоном 8%.
Примечание. Цена выражена как цена на 100 д.е. номинальной стоимости.
Точка на траектории представляет собой чистую стоимость облигации на данный момент времени. Чистая стоимость облигации (англ. 'carrying value') - это цена покупки плюс амортизированная сумма дисконта, если облигация приобретается по цене ниже номинала. Если облигация приобретается по цене выше номинала (т.е. с премией), чистая стоимость равна цене покупки за вычетом амортизированной суммы премии.
Амортизированная сумма (англ. 'amortized amount') за каждый год - это изменение цены между двумя точками на траектории цен.
Первоначальная цена облигации равна 85.503075 на 100 номинальной стоимости. Цена (чистая стоимость) через 1 год, рассчитанная на основе исходной доходности к погашению 10.40%, составляет 86.393394.
Следовательно, амортизированная сумма за первый год равна:
0.890319 (= 86.393394 - 85.503075).
Цена облигации в Примере 2 увеличивается с 85.503075 до 89.668770, и это увеличение в течение четырех лет является движением вдоль траектории цен постоянной доходности. На момент продажи облигации ее чистая стоимость также составляет 89.668770, поэтому нет прироста или убытка капитала.
Примеры 3 и 4 демонстрируют влияние процентных ставок на реализованную доходность горизонта, когда процентные ставки увеличиваются на 100 базисных пунктов (б.п.). Рыночная ставка дисконтирования по облигациям увеличивается с 10.40% до 11.40%. Ставки реинвестирования купонов также увеличиваются на 100 б.п.
Пример (2) расчета доходности инвестора по облигации.
Долгосрочный инвестор приобретает 10-летнюю облигацию с годовым купоном 8% по цене 85.503075. С момента приобретения облигации до получения первого купона процентные ставки выросли до 11.40%.
Будущая стоимость купонов, реинвестированных по ставке 11.40% на 10 лет, составляет 136.380195 на 100 д.е. номинальной стоимости.
\( \begin{aligned} \dst
8 \times 1.1140^9+ 8 \times 1.1140^8+ 8 \times 1.1140^7+ 8 \times 1.1140^6+ \\
8 \times 1.1140^5+ 8 \times 1.1140^4+ 8 \times 1.1140^3+ 8 \times 1.1140^2+ \\
8 \times 1.1140^1+ 8 = 136.380195
\end{aligned} \)
Общий доход составляет 236.380195 (= 136.380195 + 100). Реализованная ставка доходности инвестора составляет 10.70%.
\( \dst
85.503075 = {236.380195 \over (1+r)^{10}}, \ r = 0.1070
\)
В Примере 3 долгосрочный инвестор получает выгоду от более высокой ставки реинвестирования купонов. Реализованная доходность горизонта составляет 10.70%, что на 30 б.п. выше, чем результат в Примере 1, где процентные ставки были неизменны.
Прироста или убытка капитала нет, потому что облигация удерживается до наступления срока погашения. Чистая стоимость на дату погашения равна номинальной стоимости, а также сумме погашения.
Пример (4) расчета дохода инвестора по облигации.
Второй инвестор покупает 10-летнюю облигацию с годовым купоном 8% по цене 85.503075 и продает ее через четыре года. После приобретения облигации процентные ставки выросли до 11.40%. Через четыре года будущая стоимость купонов, реинвестированных под 11.40%, составит 37.899724 на 100 д.е. номинала.
\( \begin{aligned} \dst
8 \times 1.1140^3+ 8 \times 1.1140^2+ 8 \times 1.1140^1+ 8 = 37.899724
\end{aligned} \)
Цена продажи облигации через 4 года составляет 85.780408.
\( \begin{aligned} \dst
&{8 \over 1.1140^1}+ {8 \over 1.1140^2}+ {8 \over 1.1140^3}+ {8 \over 1.1140^4}+ \\
&{8 \over 1.1140^5}+ {108 \over 1.1140^6} = 85.780408
\end{aligned} \)
Общий доход составляет 123.680132 (= 37.899724 + 85.780408), что означает реализованную четырехлетнюю доходность горизонта 9.67%.
\( \dst
85.503075 = {123.680132 \over (1 + r)^4}, \ \ r = 0.0967
\)
В Примере 4 второй инвестор имеет более низкую реализованную ставку доходности по сравнению с инвестором в Примере 2, в котором процентные ставки неизменны.
Будущая стоимость реинвестированных купонных платежей увеличивается на 0.552613 (= 37.899724 - 37.347111) на 100 номинальной стоимости из-за более высоких процентных ставок.
Убыток капитала составляет 3.888362 (= 89.668770 - 85.780408) на 100 д.е. номинальной стоимости. Обратите внимание, что убыток капитала оценивается на основе чистой стоимости облигации или точки на траектории цен постоянной доходности, а не на основе первоначальной цены покупки.
На текущий момент облигация продается по цене ниже траектории цен постоянной доходности. Снижение реализованной четырехлетней доходности горизонта с 10.40% до 9.67% является результатом того, что убыток капитала превышает прибыль от реинвестирования купонов по более высокой ставке, что снижает общий доход инвестора.
Примеры 5 и 6 завершают серию расчетов ставки доходности для двух инвесторов. Процентные ставки снижаются на 100 б.п. Требуемая доходность облигации падает с 10.40% до 9.40% после покупки облигации. Процентные ставки, по которым реинвестируются купонные платежи также снижаются.
Пример 5.
Долгосрочный инвестор покупает 10-летнюю облигацию за 85.503075 и удерживает ее до погашения. С момента приобретения облигации до получения первого купона процентные ставки снижаются до 9.40%.
Будущая стоимость купонных платежей, реинвестированных под 9.40% на 10 лет, составляет 123.888356 на 100 д.е. номинальной стоимости.
\( \begin{aligned} \dst
&8 \times 1.0940^9+ 8 \times 1.0940^8+ 8 \times 1.0940^7+ 8 \times 1.0940^6+ \\
&8 \times 1.0940^5+ 8 \times 1.0940^4+ 8 \times 1.0940^3+ 8 \times 1.0940^2+ \\
&8 \times 1.0940^1+ 8 = 123.883356
\end{aligned} \)
Общий доход равен сумме будущей стоимости реинвестированных купонов и сумме погашения по номинальной стоимости, что составляет 223.883356,. Реализованная ставка доходности инвестора составляет 10.10%.
\( \dst
85.503075 = {223.888356 \over (1+r)^{10}}, \ \ r = 0.1010
\)
В Примере 5 долгосрочный инвестор сталкивается с более низкими ставками реинвестирования купонов. Реализованная доходность горизонта составляет 10.10%, что на 30 б.п. ниже результата в Примере 1, где процентные ставки не меняются.
Прироста или убытка капитала нет, потому что облигация удерживается до наступления срока погашения. Примеры 1, 3 и 5 указывают на то, что риск процентных ставок для долгосрочного инвестора возрастает исключительно за счет изменения ставок реинвестирования купонов.
Пример 6.
Второй инвестор покупает 10-летнюю облигацию за 85.503075 и продает ее через 4 года. После приобретения облигации процентные ставки снижаются до 9.40%. Будущая стоимость реинвестированных под 9.40% купонов составляет 36.801397 на 100 д.е. номинальной стоимости.
\( \begin{aligned} \dst
8 \times 1.0940^3+ 8 \times 1.0940^2+ 8 \times 1.0940^1+ 8 = 36.801397
\end{aligned} \)
Это снижение будущей стоимости компенсируется более высокой ценой продажи облигации, которая составляет 93.793912 на 100 д.е. номинальной стоимости.
\( \begin{aligned} \dst
&{8 \over 1.0940^1}+ {8 \over 1.0940^2}+ {8 \over 1.0940^3}+ {8 \over 1.0940^4}+ \\
&{8 \over 1.0940^5}+ {8 \over 1.0940^6} = 93.793912
\end{aligned} \)
Общий доход составляет 130.595309 (= 36.801397 + 93.793912), а реализованная доходность составляет 11.17%.
\( \dst
85.503075 = {130.595309 \over (1+r)^4}, \ r = 0.1117
\)
В Примере 6 инвестор имеет прирост капитала 4.125142 (= 93.793912 - 89.668770). Прирост капитала оценивается по чистой стоимости, точке на траектории цен постоянной доходности.
Этот доход влияет на снижение будущей стоимости реинвестированных купонов, увеличивая ее на 0.545714 (= 37.347111 - 36.801397). Общий доход выше, чем в Примере 2, в котором процентная ставка остается на уровне 10.40%.
В этих примерах процентный доход инвестора связан с течением времени. Таким образом, процентный доход включает в себя получение купонов, реинвестирование денежных потоков от купонов и амортизацию дисконта от покупки по цене ниже номинальной стоимости (или премии при покупке по цене выше номинала).
Прирост или убыток капитала - это доход инвестора, связанный с изменением стоимости ценной бумаги. Для облигаций с фиксированной ставкой изменение стоимости возникает в результате изменения доходности к погашению, которая является подразумеваемой рыночной ставкой.
На практике то, как процентный доход и прирост или убыток капитала рассчитываются и представляются в финансовой отчетности, зависит от финансового и налогового бухгалтерского учета.
Приведенные выше примеры иллюстрируют важную особенность облигаций с фиксированной ставкой: инвестиционный горизонт лежит в основе понимания доходности и риска процентных ставок этих облигаций. Существуют два компенсирующих типа риска процентных ставок, которые влияют на инвестора облигаций:
- риск реинвестирования купонов и
- риск рыночной цены.
Будущая стоимость реинвестированных купонных платежей (и основная сумма облигаций, которые погашаются до конечной даты инвестиционного горизонта), увеличивается, когда процентные ставки растут, и снижается, когда ставки снижаются.
Цена продажи облигации, которая погашается после конечной даты горизонта (и, следовательно, должна быть продана), уменьшается, когда процентные ставки растут, и увеличивается, когда ставки снижаются.
Риск реинвестирования купона имеет большее значение, когда инвестор имеет более долгосрочный горизонт по сравнению с оставшимся сроком погашения облигации.
Например, долгосрочный инвестор испытывает только риск реинвестирования купонов.
Риск рыночной цены имеет большее значение для инвестора с более краткосрочным горизонтом по сравнению со сроком погашения облигации. Например, инвестор, который продает облигацию до получения первого купона, испытывает только риск рыночной цены.
Следовательно, два инвестора, удерживающие одну и ту же облигацию (или портфель облигаций), могут подвергаться разному риску процентных ставок, если у них разные инвестиционные горизонты.
Пример (7) расчета цены покупки и доходности облигации.
Инвестор покупает 4-летнюю облигацию с 10% годовым купоном по цене 5.00%. Инвестор планирует продать эту облигацию через 2 года после получения второго купона.
Рассчитайте цену покупки облигации и доходность горизонта, предполагая, что ставка реинвестирования купона после покупки облигации и доходность к погашению на момент продажи составят: (1) 3,00%, (2) 5,00% и (3) 7,00%.
Решение:
Цена покупки равна 117.729753.
\( \begin{aligned} \dst
&{10 \over 1.0500^1}+ {10 \over 1.0500^2}+ \\
&{10 \over 1.0500^3}+ {10 \over 1.0500^4} = 117.729753
\end{aligned} \)
1. 3.00%: будущая стоимость реинвестированных купонов составляет 20.300.
\( 10 \times 1.0300 + 10 = 20.300 \)
Цена продажи облигации составляет 113.394288.
\( \dst {10 \over 1.0300^1}+ {10 \over 1.0300^2} = 113.394288 \)
Общий доход:
20.300 + 113.394288 = 133.694288.
Если процентные ставки снизятся с 5.00% до 3.00%, реализованная ставка доходности в течение 2-летнего инвестиционного горизонта составляет 6.5647%, что выше первоначальной доходности к погашению 5.00%.
\( \dst
117.729753 = {133.694288 \over (1+r)^2}, \ \ r = 0.065647
\)
2. 5.00%: будущая стоимость реинвестированных купонов составляет 20.500.
\( 10 \times 1.0500 + 10 = 20.500 \)
Цена продажи облигации составляет 109.297052.
\( \dst {10 \over 1.0500^1}+ {10 \over 1.0500^2} = 109.297052 \)
Общий доход:
20.500 + 109.297052 = 129.797052.
Если процентные ставки останутся на уровне 5.00% для реинвестированных купонов и требуемой доходности облигации, реализованная ставка доходности в течение 2-летнего инвестиционного горизонта будет равна доходности к погашению 5.00%.
\( \dst
117.729753 = {129.797052 \over (1+r)^2}, \ \ r = 0.050000
\)
3. 7.00%: будущая стоимость реинвестированных купонов составляет 20.700.
\( 10 \times 1.0700 + 10 = 20.700 \)
Облигация продается за 105.424055.
\( \dst {10 \over 1.0700^1}+ {10 \over 1.0700^2} = 105.424055 \)
Общий доход:
20.700 + 105.424055 = 126.124055.
\( \dst
117.729753 = {126.124055 \over (1+r)^2}, \ \ r = 0.035037
\)
Если процентные ставки вырастут с 5.00% до 7.00%, реализованная ставка доходности в течение 2-летнего инвестиционного горизонта составит 3.5037%, что ниже, чем доходность к погашению 5.00%.
