CFA - Эффективный средний срок погашения облигаций

Один из подходов к оценке риска процентной ставки по облигации заключается в оценке процентного изменения цены, с учетом изменения кривой базовой доходности, например, кривой доходности гособлигации.

Этот показатель, расчет которого очень похож на формулу для приблизительной оценки модифицированной дюрации, называют эффективным средним сроком погашения или эффективной дюрацией (англ. 'effective duration').

Эффективная дюрация облигация - это чувствительность цены облигации к изменению кривой базовой доходности. Расчета эффективной дюрации (EffDur) выполняется с помощью Формулы 9.

Разница между приблизительной модифицированной дюрацией и эффективной дюрацией заключается в знаменателе.

Модифицированная дюрация - это показатель дюрации доходности в том смысле, что он оценивает риск процентных ставок с точки зрения изменения собственной доходности к погашению облигации к сроку (\(\Delta{\rm Yield}\)).

Эффективная дюрация - это показатель дюрации кривой в том смысле, что он оценивает риск процентных ставок с точки зрения параллельного сдвига на кривой базовой доходности (\(\Delta{\rm Curve}\)).

Эффективная дюрация необходима для оценки риска процентной ставки комплексных облигаций, таких как отзывная облигация со встроенным опционом на досрочное погашение (колл-опцион). Дюрация облигации с колл-опционом не отражает чувствительность цены к изменению доходности при исполнении опциона (т.е. доходность при первом отзыве, доходность при втором отзыве и т.д.).

Проблема в том, что будущие денежные потоки неопределенны, поскольку они зависят от будущих процентных ставок. Решение эмитента об отзыве облигации (исполнении опциона) зависит от способности рефинансировать долг по более низкой стоимости.

Проще говоря, у отзываемой облигации нет четко определенной внутренней нормы прибыли (доходности к погашению). Следовательно, показатели дюрации доходности, такие как модифицированная дюрация и дюрация Маколея, к ней не применяются. Однако, эффективная дюрация является подходящим показателем дюрации.

Некоторые модели оценки опционов, которые используются для получения исходных данных при расчете эффективной дюрации для отзывной облигации, рассматриваются в следующих темах. Однако, в качестве примера, предположим, что полная цена отзывной облигации составляет 101.060489 на 100 ед. номинальной стоимости.

Исходные данные модели оценки опционов включают:

Затем аналитик фиксирует первые четыре параметра и увеличивает / уменьшает пятый параметр. Предположим, что если кривую доходности гособлигаций увеличить и уменьшить на 25 б.п., новые полные цены отзывной облигации, полученные из модели оценки, составляют 99.050120 и 102.890738 соответственно.

Следовательно, \(PV_0\) = 101.060489, \(PV_+\) = 99.050120, \(PV_-\) = 102.890738 и \(\Delta{\rm Curve}\) = 0.0025. Эффективная дюрация отзывной облигации составляет 7.6006.

\( \dst {\rm EffDur} = {102.890738 - 99.050120 \over 2 \times 0.0025 \times 101.060489 } = 7.6006 \)

Этот показатель дюрации кривой указывает на чувствительность облигации к кривой базовой доходности, при постоянном кредитном спреде.

На практике эмитент отзывной облигации может исполнить колл-опцион и получить более низкую стоимость финансирования, если:

1. базовая доходность снижается, а кредитный спред не меняется по отношению к базовой доходности или
2. базовая доходность не меняется, а кредитный спред уменьшается (например, из -за обновления кредитного рейтинга эмитента).

Модель оценки можно использовать для определения показателя «кредитной дюрации», то есть чувствительности цены облигации к изменению кредитного спреда. При традиционной облигации с фиксированной ставкой модифицированная дюрация оценивает процентное изменение цены для изменения базовой доходности и/или кредитного спреда.

Для облигаций, которые не имеют четко определенной внутренней нормы прибыли, поскольку будущие денежные потоки не являются фиксированными (например, отзывные облигации и облигации с плавающей ставкой), модели оценки используются для определения показателей изменений в базовых процентных ставках и изменений в кредитном риске.

Еще одним видом ценных бумаг с фиксированной доходностью, для которых не актуальны показатели дюрации доходности (такие как модифицированная дюрация и дюрация Маколея), являются ипотечные облигации. Эти ценные бумаги возникают в результате секьюритизации портфеля жилищной (или коммерческой) ипотеки.

Ключевым моментом для оценки риска процентной ставки по ипотечной облигации, является то, что денежные потоки зависят от способности домовладельцев рефинансировать свой долг по более низкой ставке. По сути, у домовладельцев есть колл-опционы по их ипотечным кредитам.

Практическая выгода от использования эффективной дюрации заключается в определении изменения кривой базовой доходности. При использовании приблизительной модифицированной дюрации точность улучшается за счет выбора меньшего значения изменения доходности к погашению.

Но модели оценки для более комплексных ценных бумаг, таких как облигации, обеспеченные ипотекой, включают допущения об определенном поведении корпоративных эмитентов, компаний или домовладельцев.

Процентные ставки, как правило, требуется изменить на некоторое минимальное значение, чтобы повлиять на решение отозвать облигацию или рефинансировать ипотечный кредит, поскольку выпуск нового долга несет в себе операционные затраты. Следовательно, оценка риска процентных ставок с использованием эффективной дюрации не обязательно улучшается за счет выбора меньшего изменения базовых ставок.

Эффективная дюрация стала важным инструментом в финансовом анализе не только для традиционных облигаций, но и для финансовых обязательств. Пример 9 демонстрирует такое применение эффективной дюрации.

Пример (9) расчета эффективной дюрации по обязательствам пенсионной программы.

Пенсионные программы с установленными выплатами обычно выплачивают пенсионерам ежемесячную сумму, основанную на уровне их заработной платы при выходе на пенсию.

Сумма может быть фиксирована в номинальных значениях или индексироваться в зависимости от инфляции. Эти программы называются «пенсионными программами с установленными выплатами» в стандарты учета US GAAP или МСФО.

Британская пенсионная программа стремится оценивать чувствительность своих пенсионных обязательств к изменениям процентных ставок на рынке.

Менеджер пенсионной программы нанимает актуарного консультанта для моделирования приведенной стоимости пенсионных обязательств в соответствии с тремя сценариями изменения процентных ставок:

• (1) базовая ставка 5%,
• (2) увеличение ставок на 100 б.п., до 6% и
• (3) уменьшение ставок на 100 б.п. до 4%.

Актуарий использует сложную модель оценки, которая включает в себя предположения о сохранении занятости работников, досрочном выходе на пенсию, росте заработной платы, смертности и продолжительности жизни. Следующая таблица показывает результаты анализа.

Предположение о процентной ставке	Приведенная стоимость обязательств
4%	GBP973.5 млн.
5%	GBP926.1 млн.
6%	GBP871.8 млн.

Вычислите эффективную дюрацию по обязательствам пенсионной программы.

---

Решение:

\(PV_0\) = 926.1, \(PV_+\) = 871.8, \(PV_-\) = 973.5 и \(\Delta{\rm Curve}\) = 0.0100.

Эффективная дюрация обязательств пенсионной программы составляет 5.49.

\( \dst {\rm EffDur} = {973.5 - 871.8 \over 2 \times 0.0100 \times 926.1 } = 5.49 \)

Этот показатель эффективной дюрации для обязательств пенсионной программы может использоваться при принятии решений о распределении активов, чтобы определить сочетание инвестиций в акции, инструменты фиксированного дохода и альтернативные активы.

---

Хотя эффективная дюрация является наиболее подходящим показателем оценки риска процентной ставки для облигаций со встроенными опционами, она также полезна для традиционных облигаций в дополнение к дюрации Маколея и модифицированной дюрации.

Иллюстрация 5 показывает страницу анализа доходности и спреда Bloomberg (YAS) для 2.875% казначейской облигации США с погашением 15 мая 2028 года.

Иллюстрация 5. Страница анализа доходности и спреда Bloomberg (YAS) для 2.875% казначейской облигации США.

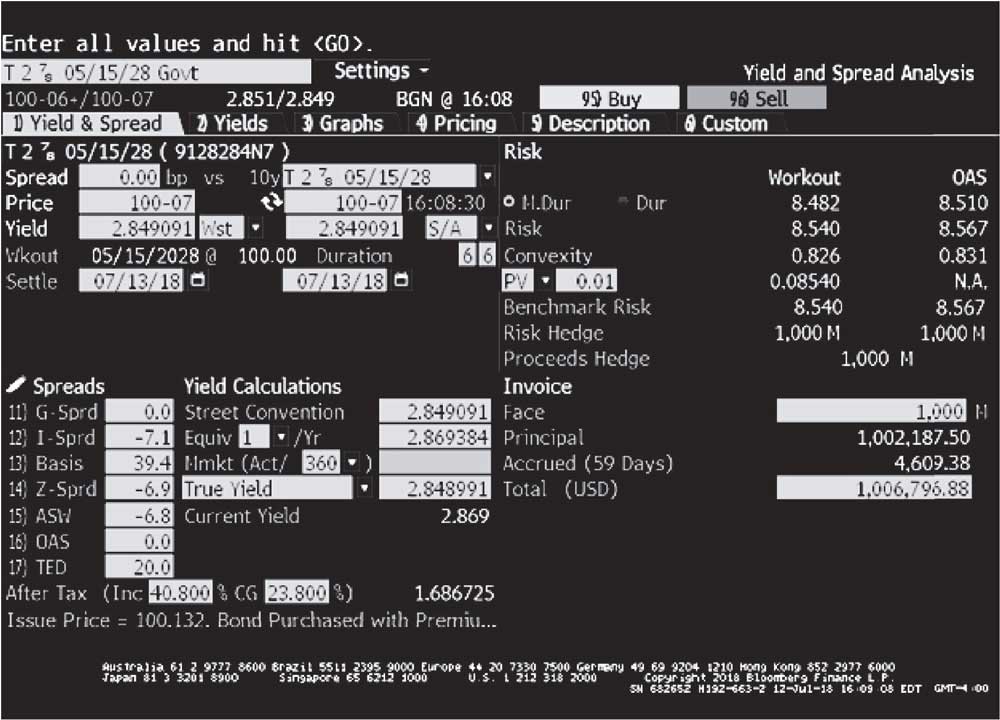
Страница анализа доходности и спреда Bloomberg (YAS) для 2.875% казначейской облигации США.

В Иллюстрации 5 котировка запрошенной цена за облигацию составляет 100-07, что равно 100 и 7/32 на 100 ед. номинальной стоимости на 13 июля 2018 года. Большинство цен на облигации обычно указываются в десятичных цифрах, но гособлигации США обычно котируются в дробных значениях.

В десятичном эквиваленте эта цена составляет 100.21875. Начисление процентов выполняется с использованием метода «фактические/фактические дни» для подсчета дней. Дата урегулирования (котировки) приходится на 59 день в 184-дневном периоде полугодового купона.

Начисленные проценты составляют 0.4609375 на 100 ед. номинальной стоимости (= 59/184 \(\times\) 0.02875/2 \(\times\) 100). Полная цена облигации составляет 100.679688. Доходность к погашению облигации составляет 2.849091% (в полугодовом исчислении).

Модифицированная дюрация облигации в Иллюстрации 5 составляет 8.482, что является обычным показателем дюрации доходности. Однако, дюрация кривой составляет 8.510, что является чувствительностью цены к изменениям в кривой доходности казначейской облигации.

У Bloomberg эффективная дюрация называется «OAS duration», поскольку она основана на модели оценки опционов, которая также используется для расчета спреда с поправкой на опцион (option-adjusted spread). Небольшая разница возникает из-за того, что кривая доходности гособлигаций не является плоской.

Когда кривая сдвинута в модели, спотовая кривая (кривая срочных ставок) также сдвигается, хоть и не в той же «параллельной» манере. Следовательно, изменение цены облигаций будет не совсем такое же, каким было бы, если бы собственная доходность к погашению облигации изменилась на то же значение, что и изменение кривой.

В целом, модифицированная дюрация и эффективная дюрация для традиционной облигации без опциона не идентичны. Разница становится меньше, когда кривая доходности является более плоской, оставшийся срок погашения короче, а облигация оценивается ближе к номиналу (поэтому разница между ставкой купона и доходностью к погашению становится меньше).

Модифицированная дюрация и эффективная дюрация по облигации без опционов идентичны только в редких обстоятельствах, при абсолютно плоской кривой доходности.

Дюрация ключевой ставки.

В примере выше эффективная дюрация для отзывной облигации рассчитывалась следующим образом:

\( \dst {\rm EffDur} = {102.890738 - 99.050120 \over 2 \times 0.0025 \times 101.060489 } = 7.6006 \)

Этот показатель дюрации указывает на чувствительность облигации к кривой базовой доходности, с учетом того, что доходность меняется на одинаковое значение. Дюрация «ключевой ставки» дает дополнительную информацию о чувствительности облигации к изменениям кривой базовой доходности.

Дюрация ключевой ставки или частичная дюрация (англ. 'key rate duration', 'partial duration') является показателем чувствительности облигации к изменению кривой базовой доходности в определенном сегменте срока погашения. В отличие от эффективной дюрации, дюрация ключевой ставки помогает определить «форму риска» для облигации, то есть ее чувствительность к изменениям в форме кривой базовой доходности (например, кривая становится более крутой или более плоской).

Предыдущая иллюстрация эффективной дюрации предполагала параллельный сдвиг на 25 б.п. при всех сроках погашения. Тем не менее, аналитик может захотеть узнать, как может измениться цена отзывной облигации, если базовые ставки для коротких сроков погашения (например, до 2 лет) сдвинутся на 25 б.п., но более ставки для более долгих сроков останутся неизменными.

Этот сценарий будет означать более плоскую кривую доходности, учитывая, что кривая доходности наклонена вверх.