CFA - Фиктивные переменные в множественной линейной регрессии
Рассмотрим определение, интерпретацию и визуализацию фиктивных переменных в множественной линейной регрессии, а также проверку статистической значимости регрессионной модели с помощью фиктивных переменных, - в рамках изучения количественных методов по программе CFA (Уровень II).
Финансовым аналитикам часто приходится использовать качественные переменные (англ. 'qualitative variables') в качестве независимых переменных в регрессии. Одним из типов таких переменных является фиктивная переменная (англ. 'dummy variable').
Фиктивная переменная принимает значение 1, если конкретное условие истинно, и 0, если это условие является ложным. Далее мы увидим, что одной из целей использования фиктивных переменных является разделение данных на «группы» или «категории».
Определение фиктивной переменной.
Фиктивная переменная может появиться в наборе данных несколькими способами:
- Она может отражать неотъемлемое свойство данных (например, принадлежность к отрасли или региону). Например, компания принадлежит отрасли здравоохранения (фиктивная переменная = 1), или нет (фиктивная переменная = 0).
Данные о таких переменных собираются непосредственно вместе с остальными независимыми переменными для каждого наблюдения. - Она может быть идентифицированной характеристикой данных. Мы можем ввести такую двоичную переменную с помощью условия, которое является либо истинным, либо ложным. Например, дата может быть до 2008 года (до начала финансового кризиса, фиктивная переменная = 0) или после 2008 года (после начала финансового кризиса, фиктивная переменная = 1).
- В качестве альтернативы она может быть построена на основе некоторой характеристики данных. Фиктивная переменная будет отражать условие, которое является либо истинным, либо ложным. Примером является удовлетворение условия, такого как размер компании (фиктивная переменная = 1, если доходы превышают €1 млрд., в противном случае она равна 0).
Нужно проявлять осмотрительность при выборе количества фиктивных переменных в регрессии. Если мы хотим провести различия между \(n\) категориями, нам нужно \(n-1\) фиктивных переменных. Таким образом, если мы используем фиктивные переменные для обозначения компаний, принадлежащих к одной из 11 отраслей, то нам потребуется 10 фиктивных переменных.
Мы по-прежнему анализируем все 11 категорий, но та категория, которой мы не назначаем фиктивную переменную, будет считаться «базовой» или «контрольной» группой. Если, например, мы хотим проанализировать данные с тремя типами взаимных фондов, то нам нужны две фиктивные переменные.
Причина необходимости использования \(n-1\) фиктивных переменных заключается в том, что мы не должны нарушать допущение 2, которое заключается в том, что между двумя или более независимыми переменными не должно существовать точной линейной связи.
Если бы мы совершили ошибку, включив в модель фиктивные переменные для всех категорий \(n\), а не \(n-1\), процедура построения модели регрессии была бы неудачной из-за полного нарушения допущения 2.
Визуализация и интерпретация фиктивных переменных.
Одним из наиболее распространенных типов фиктивных переменных являются так называемые фиктивные переменные точки пересечения (англ. 'intercept dummies') линии регрессии. Рассмотрим регрессионную модель для зависимой переменной \(Y\), которая включает одну непрерывную независимую переменную (\(X\)) и одну фиктивную переменную (\(D\)).
\( Y = b_0 + d_0 D + b_1 X + \epsilon \). (5)
Эту регрессионную модель с одной переменной можно представить как оценку двух линий наилучшего соответствия регрессии, соответствующих значениям фиктивной переменной:
- Если \(D = 0\), то уравнение принимает форму \( Y = b_0 + b_1 X + \epsilon \).
- Если \(D = 1\), то уравнение принимает форму \( Y = (b_0 + d_0) + b_1 X + \epsilon \).
В Иллюстрации 4 показано графическое представление этой модели. Этот сценарий можно интерпретировать как смещение точки пересечения на расстояние \(d_0\).
Смещение может быть положительным или отрицательным (в иллюстрации оно положительно).
Линия, при которой фиктивная переменная принимает значение ноль (\(D = 0\)), относится к базовой категории; другая линия, при которой фиктивная переменная принимает значение 1 (\(D = 1\)), относится к категории, к которой мы применяем фиктивную переменную.
Иллюстрация 4. Фиктивная переменная точки пересечения.
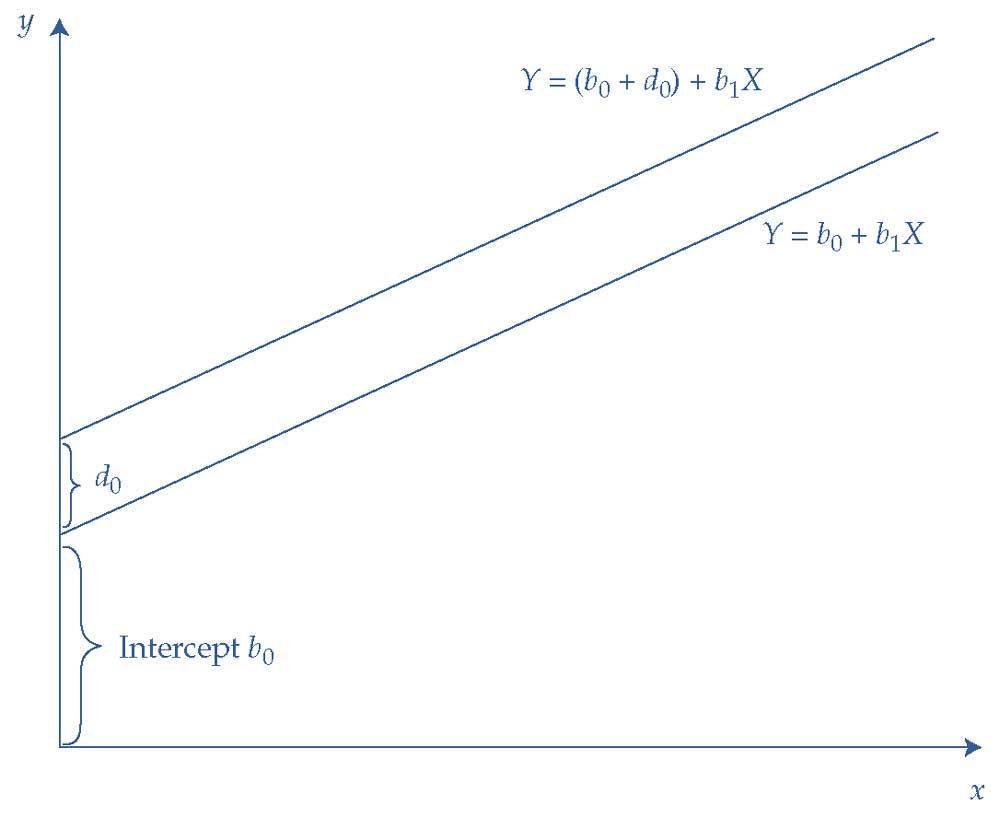
Иллюстрация 4. Фиктивная переменная точки пересечения.
Другой сценарий будет отражать фиктивные переменные, которые допускают различия в наклоне линии регрессии. Мы будем называть их фиктивными переменными наклона (англ. 'slope dummies').
Их можно объяснить, используя простую модель с одной непрерывной переменной (\(X\)) и одной фиктивной переменной (\(D\)).
\( Y = b_0 + b_1 X + d_1 ( D \times X) + \epsilon \). (6)
Присутствие такой фиктивной переменной наклона можно интерпретировать как изменение наклона между категориями, соответствующими фиктивной переменной:
- Если \(D = 0\), то \( Y = b_0 + b_1 X + \epsilon \).
- Если \(D = 1\), то \( Y = b_0 (b_1 + d_1) X + \epsilon \).
Как и прежде, случай \(D = 0\) является базовой или контрольной группой. Фиктивная переменная позволяет различать наклоны двух категорий.
Для базовой категории взаимосвязь между \(X\) и \(Y\) показана линией с менее крутым наклоном \( Y = b_0 + b_1 X \).
Для другой категории взаимосвязь между \(X\) и \(Y\) показана линией с более крутым наклоном \( Y = b_0 + (b_1 + d_1) X \).
Эта разница между наклонами может быть положительной или отрицательной в зависимости от сценария.
Иллюстрация 5. Фиктивные переменные наклона.
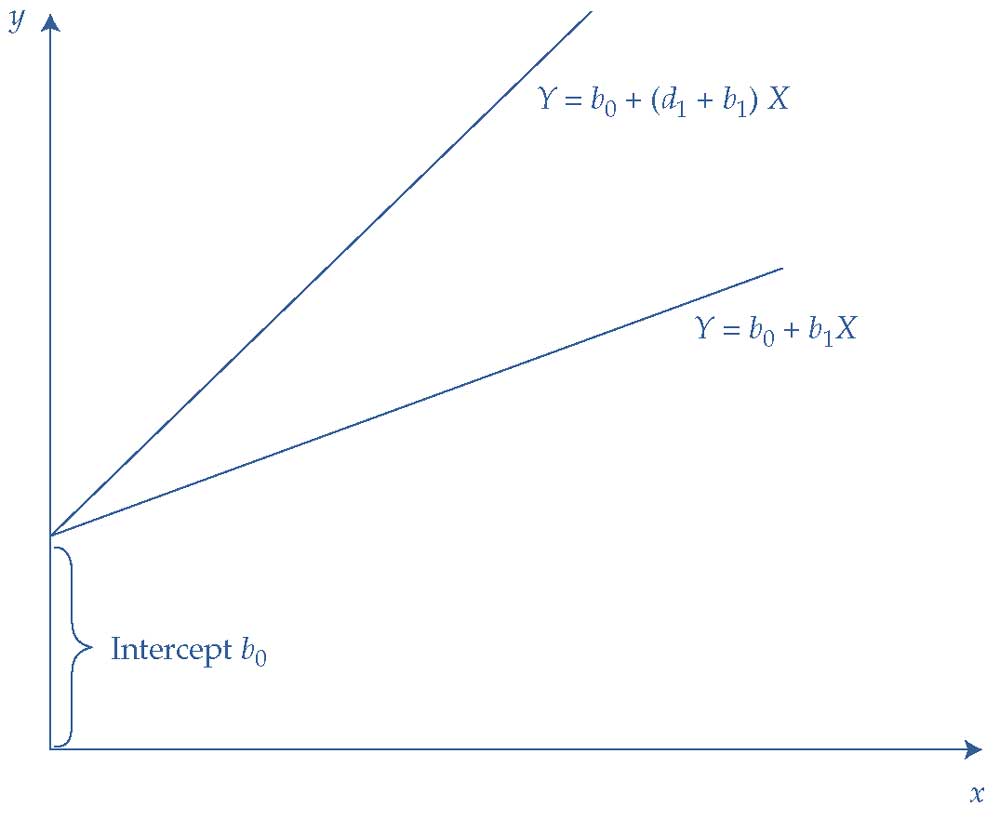
Иллюстрация 5. Фиктивные переменные наклона.
Также можно использовать фиктивные переменные, сочетающие как на наклон, так и смещение точки пересечения. Для этого мы объединяем две предыдущие модели.
Мы позволяем фиктивной переменной «взаимодействовать» с непрерывной независимой переменной \(X\).
\( Y = b_0 + d_0 D + b_1 X + d_1 ( D \times X) + \epsilon \). (7)
- Если \(D = 0\), то \( Y = b_0 + b_1 X + \epsilon \).
- Если \(D = 1\), то \( Y = (b_0 + d_0 ) + (b_1 + d_1) X + \epsilon \).
Это позволяет различать как изменение точки пересечения, так и изменение наклона в двух группах.
В этом более сложном подходе разница между двумя категориями зависит как от эффекта точки пересечения (\(d_0\)), так и от эффекта наклона (\(d_1 X\)), которые варьируются в зависимости от размера независимой переменной.
Иллюстрация 6. Фиктивные переменные наклона и точки пересчения.
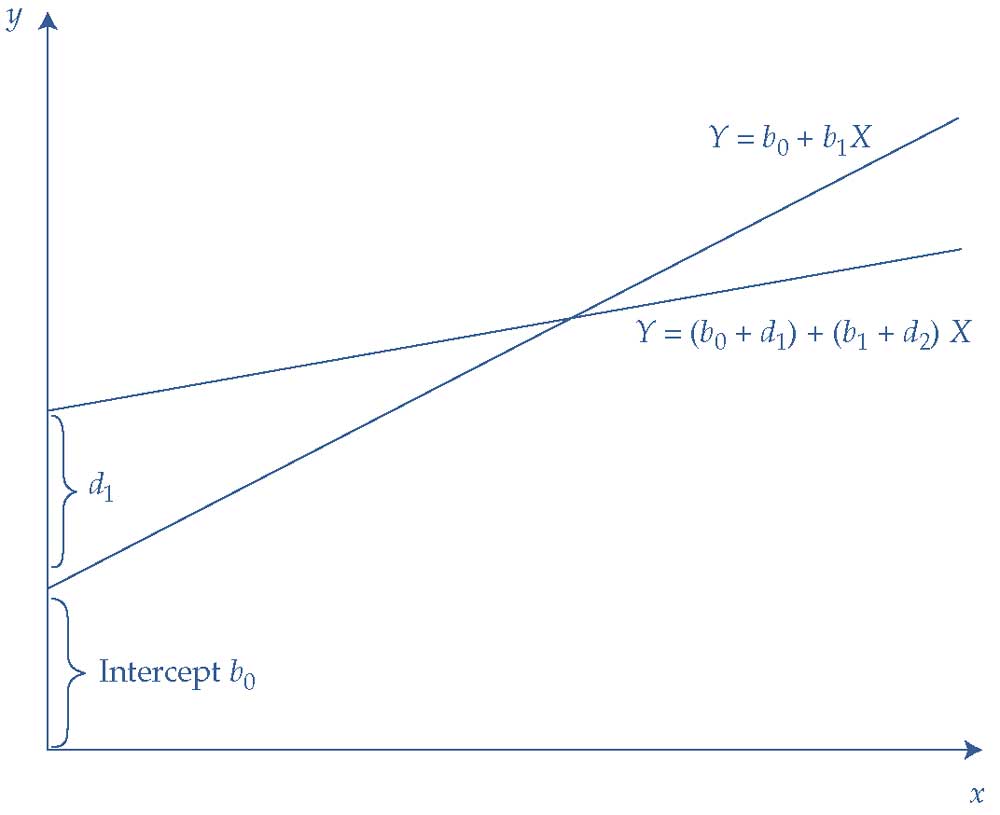
Иллюстрация 6. Фиктивные переменные наклона и точки пересчения.
Проверка на статистическую значимость с помощью фиктивных переменных.
Одной из целей использования фиктивных переменных является разделение данных на «группы» или «категории». Чтобы проверить, отличается ли функция регрессии для одной группы от другой, используются t-тесты (t-критерии) фиктивных переменных.
Отдельные t-критерии для коэффициентов фиктивных переменных указывают, насколько сильно разница между ними отличается от нуля. Иллюстрация 7 демонстрирует применение фиктивных переменных в регрессии, построенной на основе перекрестных данных взаимных фондов.
Иллюстрация 7. Анализ взаимных фондов из разных категорий.
Уильям Джеймс является аналитиком фондов в инвестиционной консультационной компании. Ему было поручено проанализировать, как характеристики взаимных фондов влияют на показатель доходности фонда, оцениваемый как средняя доходность за последние 5 лет.
Он использует большую базу данных о взаимных фондах США, которая включает в себя ряд классов стиля инвестирования.
Зависимая переменная - это среднегодовая доходность за последние 5 лет.
Независимыми переменными, выбранными аналитиком, являются коэффициент расходов фонда, натуральный логарифм размера фонда и возраста фонда, а также две фиктивные переменные для обозначения стиля фонда. Стили инвестирования - это Стоимость (Value), Смешанный (Blend) и Рост (Growth).
Поскольку имеются три категории стиля, аналитик использует \(n - 1 = 2\) фиктивные переменные.
Фиктивная переменная BLEND принимает значение 1, если наблюдение (стиль взаимного фонда) является «Смешанным», и значение 0, если это не так.
Фиктивная переменная GROWTH принимает значение 1, если фонд помечен как «Рост»; в противном случае она равна 0.
Базовая или «контрольная» категория, для которой мы не используем конкретную фиктивную переменную, - это категория «Стоимость».
В этой регрессии, мы для простоты допускаем только влияние на точку пересечения регрессии, а не на наклоны независимых переменных.
Аналитик строит следующую перекрестную регрессионную модель:
\( \begin{aligned} \dst
\text{Доходность фонда} &= b_0 + d_1 {\rm BLEND} + d_2 {\rm GROWTH} \\
&+ b_1 \text {Коэф. расходов} + b_2 \text {Средства портфеля} \\
&+ b_3 \text {Возраст фонда} + b_4 \text {Лог. активов} + \epsilon
\end{aligned} \)
Результаты расчета регрессии, показанные далее, предполагают, что, хотя \(R^2 = 0.12\) относительно низок, коэффициенты наклона статистически значимы.
Результаты показывают, что на доходность фонда негативно влияют уровень расходов и располагаемые денежные средства портфеля (коэффициенты -0.58 и -0.03 соответственно), чего мы интуитивно ожидаем. Результаты также показывают, что более старые фонды работают лучше, при положительном коэффициенте возраста 0.074.
Оценочные коэффициенты для фиктивных переменных показывают разницу между доходностью различных типов фондов.
При значениях 0.66 и 2.50 коэффициенты фиктивных переменных предполагают, что фонды категории Смешанного стиля обеспечивают среднюю доходность, которая превышает доходность фондов категории Стоимости на 0.66% в год, в то время как фонды Роста обеспечивают 2.50% сверх доходности фондов базовой категории Стоимости.
Коэффициент точки пересечения, также статистически значимый, предполагает, что среднегодовая отрицательная доходность в 2.91% является необъясненной независимыми переменными модели.
Результаты регрессии взаимных фондов.
|
Показатели регрессии |
|
|---|---|
|
\(R^2\) |
0.1230 |
|
Скорректированный \(R^2\) |
0.1228 |
|
Стандартная ошибка |
4.224 |
|
Наблюдения |
23,025 |
|
ANOVA |
df |
SS |
MS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
6 |
57,636.46 |
9,606 |
538 |
0 |
|
Остаток |
23,018 |
410,816.9 |
17.85 |
||
|
Итого |
23,024 |
468,453.3 |
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-значение |
|
|---|---|---|---|---|
|
Точка пересечения |
-2.909 |
0.299 |
-9.7376 |
2.30177E-22 |
|
Годовой коэффициент расходов |
-0.586 |
0.0495 |
-11.824 |
3.623E-32 |
|
Располагаемые денежные средства портфеля |
-0.032 |
0.0029 |
-11.168 |
6.93514E-29 |
|
Возраст фонда |
0.074 |
0.0033 |
22.605 |
6.3821E-112 |
|
Логарифм активов |
0.267 |
0.0141 |
18.924 |
2.92142E-79 |
|
Фиктивная переменная Смешанного стиля (BLEND) |
0.661 |
0.0678 |
9.749 |
2.0673E-22 |
|
Фиктивная переменная стиля Роста (GROWTH) |
2.498 |
0.0748 |
33.394 |
8.2581E-239 |
Мы также можем использовать F-тест (F-критерий) для анализа нулевой гипотезы о том, что все независимые переменные (включая фиктивные переменные) совместно равны 0.
Результаты регрессии показывают значение F-статистики равное 538. Мы сравниваем его с критическим значением. Таблица F-распределения (Приложение D) показывает критические значения для этого F-теста.
Если мы выберем уровень значимости 0.01 и посмотрим в столбец 6 (поскольку числитель имеет 6 степеней свободы), мы увидим, что критическое значение составляет 2.96, когда знаменатель имеет 120 степеней свободы.
Знаменатель фактически имеет 23,024 степеней свободы, поэтому критическое значение F-статистики меньше 2.96 (при \(df = 120\)), но больше 2.8 (при бесконечном количестве степеней свободы).
Значение статистики F-теста (F-критерия) составляет 538, поэтому мы можем отклонить нулевую гипотезу о том, что коэффициенты совместно равны 0.
Джеймс решает расширить свой анализ взаимных фондов, добавив в модель фиктивные переменные наклона. Первоначальные результаты показали взаимосвязь между доходностью и возрастом фонда, хотя величина была небольшой: 0.07% за каждый год.
Он задается вопросом, отличается ли эта связь между доходностью и возрастом среди различных типов фондов.
Например, влияет ли возрастной фактор на фонды Роста или фонды Смешанного стиля больше, чем на фонды Стоимости?
Другими словами, отличается ли улучшение доходности за счета возраста фонда среди различных типов фондов?
Чтобы изучить эту гипотезу (о том, что влияние возраста фонда различно для разных типов фондов), он вводит две дополнительные независимые переменные, одна из которых является произведением «Возраст фонда \(\times\) Фиктивная переменная BLEND», а вторая - «Возраст фонда \(\times\) Фиктивная переменная GROWTH».
Аналитик строит следующую модель:
\( \begin{aligned} \dst
\Large \substack{\text{Доходность фонда} \\ \text{(средняя за 5 лет)} }
&= b_0 + b_1 \text {Коэф. расходов} + b_2 \text {Средства портфеля} \\
&+ b_3 \text {Возраст фонда} + b_4 \text {Лог. активов} \\
&+ d_1 {\rm BLEND} + d_2 {\rm GROWTH} \\
&+ «\text {Возраст фонда} \times {\rm BLEND}» \\
&+ «\text {Возраст фонда} \times {\rm GROWTH}» + \epsilon
\end{aligned} \)
Когда фиктивная переменная BLEND равна 1, соответствующая дополнительная переменная принимает значение «Возраста фонда». Для наблюдений, в которых фиктивная переменная GROWTH равна 1, соответствующая дополнительная переменная также принимает значение «Возраста фонда». Результаты регрессии следующие:
|
Показатели регрессии |
|
|---|---|
|
\(R^2\) |
0.123 |
|
Скорректированный \(R^2\) |
0.123 |
|
Стандартная ошибка |
4.224 |
|
Наблюдения |
23,025 |
|
ANOVA |
df |
SS |
MS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
8 |
57,760.46 |
7,220 |
404.6 |
0 |
|
Остаток |
23,016 |
410,692.9 |
17.84 |
||
|
Итого |
23,024 |
468,453.3 |
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-значение |
|
|---|---|---|---|---|
|
Точка пересечения |
-2.81 |
0.306 |
-9.183 |
4.54531E-20 |
|
Годовой коэффициент расходов |
-0.587 |
0.0496 |
-11.839 |
3.0289E-32 |
|
Располагаемые денежные средства портфеля |
-0.032 |
0.0029 |
-11.211 |
4.28797E-29 |
|
Возраст фонда |
0.065 |
0.0059 |
11.012 |
3.91371E-28 |
|
Логарифм активов |
0.267 |
0.0141 |
18.906 |
4.05994E-79 |
|
Фиктивная переменная Смешанного стиля (BLEND) |
0.603 |
0.1088 |
5.546 |
2.95478E-08 |
|
Фиктивная переменная стиля Роста (GROWTH) |
2.262 |
0.1204 |
18.779 |
4.27618E-78 |
|
Возраст фонда \(\times\) BLEND |
0.0049 |
0.0077 |
0.627 |
0.530817435 |
|
Возраст фонда \(\times\) GROWTH |
0.0201 |
0.0081 |
2.478 |
0.01323 |
Результаты регрессии показывают исходные коэффициенты точки пересечения и наклона плюс новые коэффициенты наклона фиктивных переменных.
Значения и статистическая значимость коэффициента точки пересечения и наклона показывают небольшие изменения. Но пересмотренная модель предоставляет больше информации о переменной возраста фонда.
Для нашей базовой или контрольной группы (фонды Стоимости) мы наблюдаем коэффициент возраста фонда 0.065. Это предполагает, что эти фонды получают дополнительную доходность с течением времени (то есть, благодаря возрасту фонда).
В этой модели у нас также есть фиктивные переменные взаимодействия, среди которых переменная «Возраст фонда \(\times\) GROWTH» имеет статистически значимый коэффициент.
Для фондов Роста дополнительная годовая доходность с каждым дополнительным годом является суммой коэффициентов «Возраст» и «Возраст фонда \(\times\) GROWTH» (то есть, 0.065% + 0.02%).
Таким образом, общий коэффициент «наклона», воздействующий на эффективность (доходность) фондов Роста является суммой двух коэффициентов.
Один из них можно интерпретировать как общую эффективность, предполагая, что фонды Роста обеспечивают доходность, которая превышает доходность фондов Стоимости на 2.26% (точка пересечения Роста) плюс 0.085% за каждый год.
Другой способ интерпретировать этот результат - представить двухмерное пространство аналогично тому, что показано в Иллюстрации 6. Коэффициент переменной «Возраст фонда \(\times\) GROWTH» даст дополнительный наклон, подразумеваемый ростом сверх коэффициента наклона переменной «Возраст фонда».
