CFA - Ошибки спецификации регрессионной модели
Рассмотрим, как ошибки спецификации модели множественной регрессии влияют на результаты регрессионного анализа, а также как избежать типичных ошибок неправильной спецификации модели, - в рамках изучения количественных методов по программе CFA (Уровень II).
До сих пор мы предполагали, что любая регрессионная модель, которую мы оцениваем, правильно определена. Определение или спецификация модели регрессии (англ. 'model specification') - это набор переменных, включенных в регрессию, а также функциональная форма уравнения регрессии.
Сначала мы приведем некоторые общие рекомендации по правильному определению спецификации регрессии. Затем мы перейдем к трем типам ошибочной спецификации модели: неправильно определенная функциональная форма, регрессоры, которые коррелируют с членом ошибки уравнения регрессии, а также ошибочная спецификация временных рядов.
Каждый из этих типов ошибочной спецификации приводит к необоснованному статистическому выводу с использованием OLS (метода наименьших квадратов); Большинство из этих ошибок приведут к несостоятельным коэффициентам регрессии.
Принципы спецификации модели регрессии.
Обсуждая принципы спецификации модели, мы должны признать, что существуют конкурирующие взгляды на то, как подходить к спецификации модели.
Кроме того, наша цель использования регрессионного анализа может повлиять на выбранную нами спецификацию. Однако следующие принципы имеют довольно широкое общее применение.
1. Модель должна быть основана на убедительном экономическом обосновании. Мы должны быть в состоянии предоставить экономические рассуждения, стоящие за выбором переменных, и эти рассуждения должны иметь смысл.
Если это условие выполнено, мы увеличиваем вероятность того, что модель будет иметь прогностическую ценность при ее использовании с новыми данными. Этот подход контрастирует с процессом подбора переменных, известным как добыча данных или интеллектуальный анализ данных (англ. 'data mining').
С помощью интеллектуального анализа данных исследователь по существу разрабатывает модель, которая максимально использует характеристики конкретного набора данных. Термин «data mining» используется в различных смыслах при выявлении шаблонов в больших наборах данных.
2. Функциональная форма, выбранная для переменных регрессии, должна быть подходящей, учитывая характер переменных. В качестве иллюстрации этого принципа рассмотрите прогнозирование рынка взаимных фондов только на основе доходности фонда и рынка.
Веской причиной для успешного прогнозирования будет то, что график доходности взаимного фонда в сравнении с доходностью всего рынка будет показывать большую кривизну, поскольку успешный рыночный аналитик будет иметь тенденцию увеличивать (уменьшать) бета-коэффициент при высокой (низкой) рыночной доходности. Спецификация модели должна отражать эту ожидаемую нелинейную связь.
В других случаях мы можем преобразовать данные так, чтобы лучше соблюсти этот принцип и прочие допущения.
3. Модель должна быть экономной. В этом контексте «экономная модель» (parsimonious model) означает большой эффект от малого количества. Мы должны ожидать, что каждая переменная, включенная в регрессию, сыграет важную роль.
4. Модель необходимо проверить на предмет нарушений допущений регрессии, прежде чем принять ее.
Мы уже обсуждали диагностику наличия гетероскедастичности, сериальной корреляции и мультиколлинеарности.
В результате такой диагностики мы можем сделать вывод, что нам необходимо пересмотреть набор включенных в модель переменных и/или их функциональную форму.
5. Модель необходимо протестировать и убедиться в ее полезности вне выборки перед принятием. Термин «вне выборки» (out of sample) относится к наблюдениям вне набора данных, на основе которого оценивалась модель.
Правдоподобная модель может не работать вне выборки, потому что экономические взаимосвязи изменились с момента окончания периода выборки. Эта возможность сама по себе полезна.
Однако второе объяснение может заключаться в том, что взаимосвязи не изменились, но модель объясняет только конкретный набор данных.
Предоставив некоторое общее руководство по спецификации модели, мы переходим к обсуждению конкретных ошибок спецификации модели. Понимание этих ошибок поможет аналитику разработать лучшие модели и стать более информированным пользователем инвестиционных исследований.
Неправильно определенная функциональная форма.
Всякий раз, когда мы оцениваем регрессию, мы должны допустить, что регрессия имеет правильную функциональную форму. Это допущение может быть нарушено несколькими способами:
- Пропущенная переменная или переменные. Одна или несколько важных переменных могут быть не включены в регрессию.
- Неуместное масштабирование переменной. Одна или несколько переменных регрессии, возможно, требуют преобразования (например, путем нахождения натурального логарифма переменной) перед расчетом регрессии.
- Неуместное объединение данных. Регрессионные модели объединяют данные из разных выборок, которые не следует объединять.
Во-первых, рассмотрим влияние исключения важной независимой переменной из регрессии - смещение пропущенной переменной (omitted variable bias). Если истинная регрессионная модель была
\( Y_i = b_0 + b_1 X_{1i} + b_2 X_{2i} + \epsilon_i \), (10)
но мы оцениваем модель
\( Y_i = a_0 + a_1 X_{1i} + \epsilon_i \),
то наша регрессионная модель будет неправильно определена. Обратите внимание на различные обозначения, когда в модель не включается \( X_{2i} \), потому что член точки пересечения и коэффициент наклона по \( X_{1i} \), как правило, не будут такими же, как при включении в модель \( X_{2i} \).
Что не так с этой моделью?
Если пропущенная переменная (\( X_2 \)) коррелирует с оставшейся переменной (\( X_1 \)), то член ошибки в модели будет коррелировать с (\( X_1 \)), а значения коэффициентов регрессии \( a_0 \) и \( a_1 \) будут смещенными и необоснованными.
Кроме того, оценки стандартных ошибок этих коэффициентов также будут противоречивыми. Таким образом, мы не можем использовать ни оценки коэффициентов, ни оценки стандартных ошибок для проведения статистических тестов.
Иллюстрация 17. Смещение пропущенной переменной и спред цен продавца и покупателя.
В этом примере мы расширяем наше изучение спреда цен продавца и покупателя (спред bid-ask), чтобы показать эффект исключения важной переменной из регрессии.
В Иллюстрации 1 мы показали, что натуральный логарифм коэффициента [Спред bid-ask / Цена] был в значительной степени связан как с натуральным логарифмом количества участников рынка, так и с натуральным логарифмом рыночной капитализации компании.
Ниже мы повторно приводим результаты регрессии из Иллюстрации 1.
Результаты регрессии ln (Спред bid-ask / Цена) по ln (Количество участников рынка) и ln (Рыночная капитализация).
|
Коэффициент |
Стандартная |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
1.5949 |
0.2275 |
7.0105 |
|
ln (количество участников рынка NASDAQ) |
-1.5186 |
0.0808 |
-18.7946 |
|
ln (рыночная капитализация компании) |
-0.3790 |
0.0151 |
-25.0993 |
|
ANOVA |
df |
SS |
MSS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
2 |
3,728.1334 |
1,864.0667 |
2,216.75 |
0.00 |
|
Остаток |
2,584 |
2,172.8870 |
0.8409 |
||
|
Итого |
2,586 |
5,901.0204 |
|||
|
Стандартная ошибка остатка |
0.9170 |
||||
|
Множественный \( R^2 \) |
0.6318 |
||||
|
Наблюдения |
2,587 |
Примечание: «df» = степени свободы.
Источник: Центр исследований цен на акции, Чикагский университет.
Если бы мы не включили в регрессию натуральный логарифм рыночной капитализации в качестве независимой переменной и регрессировали бы натуральный логарифм коэффициента [Спред bid-ask / Цена] только по натуральному логарифму количества участников рынка для данных акций, результаты были бы такими, как показано ниже.
|
Коэффициент |
Стандартная |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
5.0707 | 0.2009 | 25.2399 |
|
ln (количество участников рынка NASDAQ) |
-3.1027 | 0.0561 | -55.3066 |
|
ANOVA |
df |
SS |
MSS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
1 |
3,200.3918 | 3,200.3918 | 3,063.3655 |
0.00 |
|
Остаток |
2,585 |
2,700.6287 | 1.0447 | ||
|
Итого |
2,586 |
5,901.0204 |
|||
|
Стандартная ошибка остатка |
1.0221 | ||||
|
Множественный \( R^2 \) |
0.5423 | ||||
|
Наблюдения |
2,587 |
Источник: Центр исследований цен на акции, Чикагский университет.
Обратите внимание, что коэффициент для ln (количество участников рынка NASDAQ) изменился с -1.5186 в исходной (правильно определенной) регрессии до -3.1027 в неправильно определенной регрессии.
Кроме того, точка пересечения изменилась с 1.5949 в правильно определенной регрессии до 5.0707 в ошибочно определенной регрессии.
Эти результаты иллюстрируют, что пропуск независимой переменной, которая должна была быть включена в регрессию, может привести к тому, что оставшиеся в регрессии коэффициенты будут необоснованными.
Второй распространенной причиной неправильной спецификации в регрессионных моделях является использование неправильной формы данных в регрессии, когда преобразованная версия данных является подходящей.
Например, иногда аналитики могут не учесть кривизну или нелинейность связи между зависимой переменной и одной или несколькими независимыми переменными, и вместо этого определяют линейную связь между переменными.
Когда мы определяем регрессионную модель, мы должны рассмотреть вопрос о том, предполагает ли экономическая теория нелинейную связь в подобном случае.
Мы часто можем подтвердить нелинейность путем построения данных, как показано ниже в Примере 2.
Если связь между переменными становится линейной, когда одна или несколько переменных представлены как пропорциональное изменение переменной, мы можем исправить неправильную спецификацию, используя натуральный логарифм переменной, которую мы хотим представить как пропорциональное изменение.
В других случаях аналитики используют в регрессиях немасштабированные данные, когда больше подходят масштабированные данные (такие как деление чистого дохода или денежного потока на выручку).
В Иллюстрации 1 мы масштабировали спред bid-ask по цене акций, потому что то, что данный спред имеет значение с точки зрения транзакционных издержек для данного размера инвестиций, зависит от цены акций. Если бы мы не масштабировали спред bid-ask, регрессия была бы неправильно определена.
Пример 2. Нелинейность и спред цен продавца и покупателя (bid-ask).
В Иллюстрации 1 мы показали, что натуральный логарифм коэффициента [Спред bid-ask / Цена] был в значительной степени связан как с натуральным логарифмом количества участников рынка, так и с натуральным логарифмом рыночной капитализации компании.
Но почему мы использовали натуральный логарифм для каждой переменной в регрессии? Мы начали обсуждение этого вопроса в Иллюстрации 1, и теперь продолжим.
Что предполагает теория о характере связи между коэффициентом [Спред bid-ask / Цена] и его детерминантами (независимые переменные)?
Stoll (1978) построил теоретическую модель детерминант процентного выражения спреда bid-ask на дилерском рынке. В его модели детерминанты вводятся мультипликативно определенным образом.
С точки зрения независимых переменных, представленных в Иллюстрации 1, предполагаемая функциональная форма будет такой:
[Спред bid-ask / Цена]\(_i\) = \(c\) (Количество участников рынка)\(_i^{b_1}\) \(\times\) (Рыночная капитализация)\(_i^{b_2}\),
где \(c\) является константой.
Связь процентного спреда bid-ask с количеством участников рынка и рыночной капитализацией не является линейной при исходных переменных (форма модели аналогична производственной функции Кобба-Дугласа).
Однако, если мы используем натуральный логарифм для обеих сторон этой модели, то получим модель регрессии log-log, которая является линейной в преобразованных переменных:
\( Y_i = b_0+ b_1 X_{1i}+ b_2 X_{2i}+ \epsilon_i \),
где
- \(Y_i\) = натуральный логарифм коэффициента [Спред bid-ask / Цена] для акции \(i\).
- \( Y_i\) = константа, равная \( \ln(c)\).
- \(X_{1i}\) = натуральный логарифм количества участников рынка для акции \(i\).
- \(X_{1i}\) = натуральный логарифм рыночной капитализации компании \(i\).
- \(\epsilon_i\) = член ошибки.
Как упомянуто в Иллюстрации 1, коэффициент наклона в модели log-log интерпретируется как эластичность, а точнее, частичная эластичность зависимой переменной относительно независимой переменной («частичная» означает, что другие независимые переменные остаются неизменными).
Мы можем построить графики, чтобы оценить, являются ли переменные линейно связаны после их логарифмического преобразования.
Например, в Иллюстрации 18 мы показываем график рассеивания натурального логарифма количества участников рынка для акции (по оси X) и натурального логарифма [Спред bid-ask / Цена] (по оси Y), а также линию регрессии, показывающую линейную связь между двумя преобразованными переменными.
Связь между двумя преобразованными переменными явно линейная.
Иллюстрация 18. Линейная регрессия, в которой две переменные имеют линейную связь.
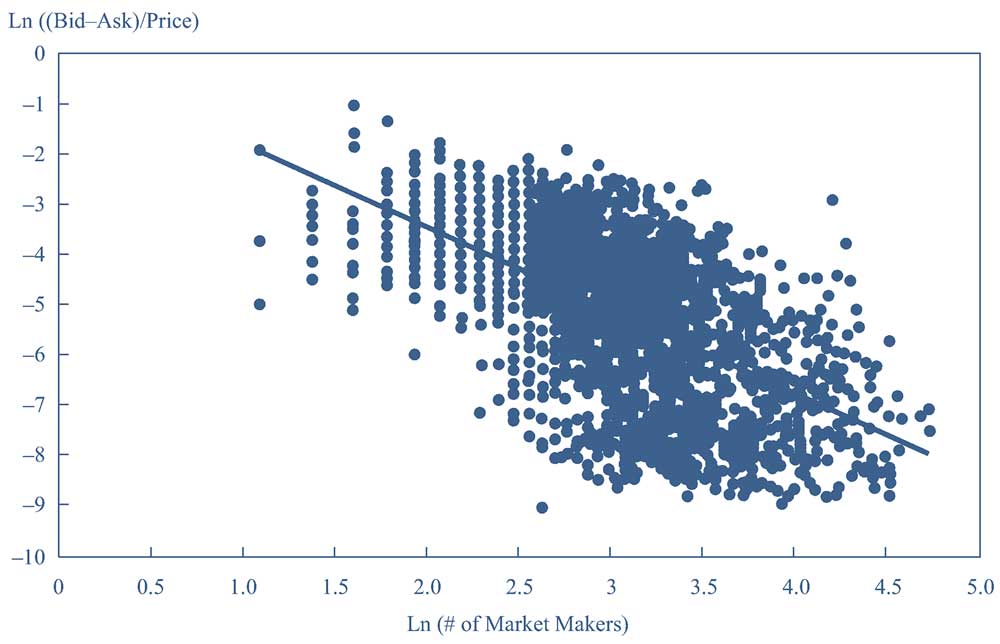
Линейная регрессия, в которой две переменные имеют линейную связь.
Иллюстрация 19. Линейная регрессия, в которой две переменные имеют нелинейную связь.
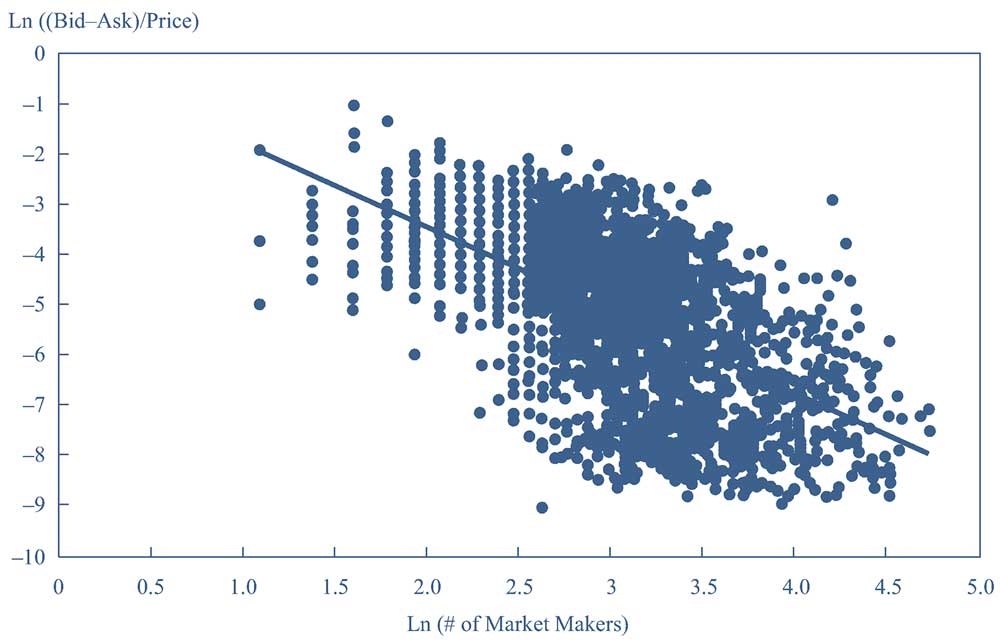
Линейная регрессия, в которой две переменные имеют нелинейную связь.
Если мы не используем логарифм коэффициента [Спред bid-ask / Цена], то график не будет линейным.
В Иллюстрации 19 показан график натурального логарифма количества участников рынка для акции (по оси X) и коэффициента [Спред bid-ask / Цена], выраженного в процентах (по оси Y), а также линия регрессии, которая пытается показать линейную связь между двумя переменными.
Мы видим, что связь между двумя переменными очень нелинейна. Обратите внимание, что связь между коэффициентом [Спред bid-ask / Цена] и ln(Рыночная капитализация) также является нелинейной, в то время как связь между ln([Спред bid-ask / Цена]) и ln(Рыночная капитализация) является линейной; мы не приводим здесь эти графики для краткости.
Следовательно, мы не должны оценивать регрессию с коэффициентом [Спред bid-ask / Цена] в качестве зависимой переменной.
Если нам нужно обеспечить, чтобы прогнозируемые спреды bid-ask были положительными, мы также не будем использовать [Спред bid-ask / Цена] в качестве зависимой переменной.
Если мы используем не преобразованный коэффициент [Спред bid-ask / Цена] в качестве зависимой переменной, то модель может предсказать отрицательные значения спреда bid-ask.
Этот результат будет бессмысленным.
В действительности, ни один спред bid-ask не является отрицательным (трудно мотивировать трейдеров одновременно покупать по высокой цене и продавать по низкой цене), поэтому модель, которая прогнозирует отрицательные спреды, безусловно, неправильно определена.
В нашей выборке данных спред bid-ask для каждой из 2,587 компаний является положительным. Далее мы проиллюстрируем проблему отрицательных значений прогнозируемых спредов bid-ask.
Иллюстрация 20 показывает результаты регрессии с коэффициентом [Спред bid-ask / Цена] в качестве зависимой переменной, а также натуральным логарифмом количества участников рынка и натуральным логарифмом рыночной капитализации компании в качестве независимых переменных.
Иллюстрация 20. Результаты регрессии коэффициента [Спред bid-ask / Цена] по ln (Количество участников рынка) и ln (Рыночная капитализация).
|
Коэффициент |
Стандартная ошибка |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
0.0674 | 0.0035 | 19.2571 |
|
ln (количество участников рынка NASDAQ) |
-0.0142 | 0.0012 | -11.8333 |
|
ln (рыночная капитализация компании) |
-0.0016 | 0.0002 | -8.0000 |
|
ANOVA |
df |
SS |
MSS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
2 |
0.1539 | 0.0770 | 392.3338 |
0.00 |
|
Остаток |
2,584 |
0.5068 | 0.0002 | ||
|
Итого |
2,586 |
0.6607 | |||
|
Стандартная ошибка остатка |
0.0140 | ||||
|
Множественный \( R^2 \) |
0.2329 | ||||
|
Наблюдения |
2,587 |
Источник: Центр исследований цен на акции, Чикагский университет.
1. Предположим, что для конкретных акций NASDAQ количество участников рынка составляет 50, а рыночная капитализация составляет $6 млрд. Каким будет предсказанный коэффициент [Спред bid-ask / Цена] для этих акций на основе только что показанной модели?
2. Имеет ли смысл прогнозируемый спред bid-ask для этих акций? Если нет, то как можно избежать этой проблемы?
Решение для части 1:
Натуральный логарифм количества участников рынка равен \( \ln 50 = 3.9120 \), а натуральный логарифм рыночной капитализации акций (в млн.) составляет \(\ln 6,000 = 8.6995\).
В этом случае прогнозируемый коэффициент [Спред bid-ask / Цена] составляет:
0.0674 + (-0.0142 \(\times\) 3.9120) + (-0.0016 \(\times\) 8.6995) = -0.0021.
Следовательно, модель предсказывает, что коэффициент [Спред bid-ask / Цена] составляет -0.0021 или -0.21% от цены акций.
Решение для части 2:
Прогнозируемый спред bid-ask отрицательный, что не имеет экономического смысла. Этой проблемы можно избежать, используя логарифм [Спред bid-ask / Цена] в качестве зависимой переменной.
Независимо от того, является ли натуральный логарифм процентного спреда bid-ask, Y, положительным или отрицательным, процентный спред bid-ask, выраженный как \(e^Y\), является положительным, поскольку положительное число, возведенное в любую степень, является положительным.
Константа \(е\) является положительной (\(е \approx 2.7183\)).
Аналитикам часто приходится решать, масштабируются ли переменные, прежде чем сравнивать данные разных компаний. Например, при анализе финансовой отчетности аналитики часто сравнивают компании, используя вертикальный или процентный анализ отчетности.
В процентном отчете о прибылях и убытках все статьи отчета делятся на выручку компании. Процентные отчеты значительно облегчают сравнительный анализ компаний.
Аналитик может использовать процентные отчеты для быстрого сравнения тенденций в валовой прибыли (или других переменных отчета о прибылях и убытках) для группы компаний.
Проблемы сопоставимости также появляются у аналитиков, которые хотят использовать регрессионный анализ для сравнения результатов группы компаний. Иллюстрация 21 демонстрирует эту проблему.
Иллюстрация 21. Масштабирование и связь между операционным и свободным денежным потоком.
Предположим, мы исследуем старые данные за 2001 год и хотим объяснить свободный денежный поток фирмы в зависимости от операционного денежного потока за 2001 год для 11 магазинов семейной одежды США с рыночной капитализацией более $100 млн. на конец 2001.
Чтобы исследовать эту проблему, аналитик может использовать свободный денежный поток в качестве зависимой переменной и операционный денежный поток в качестве независимой переменной в линейной регрессии с одной независимой переменной.
Ниже мы покажем результаты этой регрессии.
Обратите внимание, что t-статистика для коэффициента наклона операционного денежного потока довольно высока (6.5288), уровень значимости для F-статистики регрессии очень низкий (0.0001), а \(R^2\) довольно высокий.
У нас может возникнуть соблазн поверить, что эта регрессия является успешной и что для магазина семейной одежды при увеличении операционного денежного потока на $1.00 мы могли бы уверенно предсказать увеличение свободного денежного потока на $0.3579.
Результаты регрессии свободного денежного потока по операционному денежному потоку для магазинов семейной одежды.
|
Коэффициент |
Стандартная |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
0.7295 |
27.7302 |
0.0263 |
|
Операционный денежный поток |
0.3579 |
0.0548 |
6.5288 |
|
ANOVA |
df |
SS |
MSS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
1 |
245,093.7836 |
245,093.7836 |
42.6247 |
0.0001 |
|
Остаток |
9 |
51,750.3139 |
5,750.0349 |
||
|
Итого |
10 |
296,844.0975 |
|||
|
Стандартная ошибка остатка |
75.8290 |
||||
|
Множественный \( R^2 \) |
0.8257 |
||||
|
Наблюдения |
11 |
Источник: Compustat.
Но верна ли эта спецификация?
Регрессия не учитывает различия между компаниями в выборке. Но мы можем учитывать различия в размерах, используя результаты вертикального анализа отчетов о движении денежных средств по компаниям.
Мы масштабируем переменные путем деления операционного денежного потока и свободного денежного потока на выручку компании, перед проведением регрессионного анализа.
Мы будем использовать [Свободный денежный поток / Выручка] в качестве зависимой переменной и [Операционный денежный поток / Выручка] в качестве независимой переменной.
Результаты показаны далее. Обратите внимание, что t-статистика для коэффициента наклона по [Операционный денежный поток / Выручка] составляет 1.6262, поэтому он не является значимым на уровне 0.05.
Также обратите внимание, что уровень значимости F-статистики составляет 0.1383, поэтому мы не можем отклонить на уровне значимости 0.05 гипотезу о том, что регрессия не объясняет различия в коэфф. [Свободный денежный поток / Выручка] среди магазинов семейной одежды.
Наконец, обратите внимание, что \(R^2\) в этой регрессии намного ниже, чем в предыдущей регрессии.
Результаты регрессии коэфф. [Свободный денежный поток / Выручка] по коэфф. [Операционный денежный поток / Выручка] для магазинов семейной одежды.
|
Коэффициент |
Стандартная ошибка |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
-0.0121 |
0.0221 |
-0.5497 |
|
Операционный денежный поток / Выручка |
0.4749 |
0.2920 |
1.6262 |
|
ANOVA |
df |
SS |
MSS |
F |
Значимость F |
|---|---|---|---|---|---|
|
Регрессия |
1 |
0.0030 |
0.0030 |
2.6447 |
0.1383 |
|
Остаток |
9 |
0.0102 |
0.0011 |
||
|
Итого |
10 |
0.0131 |
|||
|
Стандартная ошибка остатка |
0.0336 |
||||
|
Множественный \( R^2 \) |
0.2271 |
||||
|
Наблюдения |
11 |
Источник: Compustat.
Какая регрессия имеет больше смысла?
Обычно масштабированная регрессия имеет больше смысла. Мы хотим знать, что происходит со свободным денежным потоком (в виде доли от выручки), при изменении операционного денежного потока (в виде доли от выручки).
Без масштабирования результаты регрессии могут основываться исключительно на различиях в масштабе компаний, а не в их экономике.
Третья общая форма ошибочной спецификации регрессионных моделей - объединение данных из разных выборок, которые не следует объединять. Этот тип неправильной спецификации лучше всего проиллюстрировать графически.
В Иллюстрации 22 показаны два кластера данных для переменных X и Y с подобранной линией регрессии. Например, данные могут представлять связь между двумя финансовыми переменными в два разных периода времени.
Иллюстрация 22. График регрессии для двух временных периодов с меняющимися средними значениями.
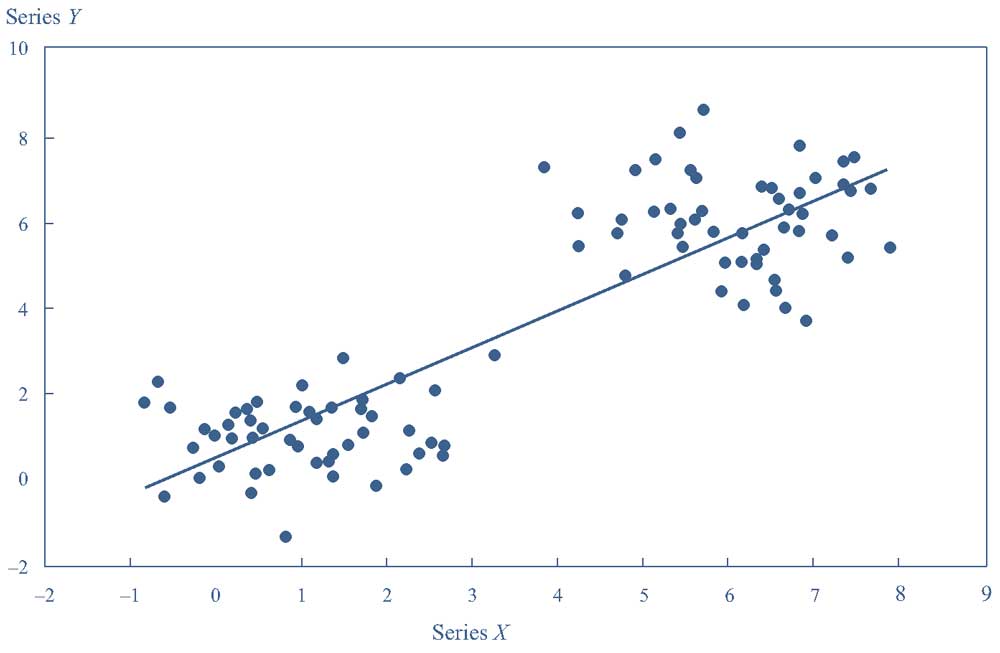
График регрессии для двух временных периодов с меняющимися средними значениями.
В каждом кластере данных X и Y корреляция между двумя переменными практически равна 0.
Поскольку средние значения как X, так и Y различны для двух кластеров данных в комбинированной выборке, X и Y сильно коррелируют.
Однако корреляция является ложной (вводящей в заблуждение), потому что она отражает различия во взаимосвязи между X и Y в течение двух разных периодов времени.
