CFA - Нарушения допущений регрессии: гетероскедастичность

Ранее мы представили допущения модели множественной линейной регрессии. Статистический вывод, основанный на предполагаемой регрессионной модели, опирается на то, что эти допущения соблюдаются.

При применении регрессионного анализа к финансовым данным аналитики должны иметь возможность диагностировать нарушения допущений регрессии, понимать последствия этих нарушений и знать шаги по исправлению нарушений.

В следующих разделах мы обсудим три нарушения регрессии: гетероскедастичность, сериальная корреляция (автокорреляция) и мультиколлинеарность.

Гетероскедастичность.

Ранее мы сделали важное допущение о том, что дисперсия ошибки в регрессии постоянна для различных наблюдений. Выражаясь в статистических терминах, мы допустили, что ошибки были гомоскедастическими (англ. 'homoskedastic').

Однако, ошибки в финансовых данных часто являются гетероскедастическими (англ. 'heteroskedastic'): дисперсия ошибок отличается для различных наблюдений. В этом разделе мы обсуждаем, как гетероскедастичность влияет на статистический анализ, как проверить регрессию на гетероскедастичность и как исправить это нарушение.

Мы можем увидеть разницу между гомоскедастическими и гетероскедастическими ошибками, сравнивая два графика. В Иллюстрации 8 показаны значения зависимых и независимых переменных и подобранную линию регрессии для модели с гомоскедастическими ошибками.

Не существует систематической взаимосвязи между значением независимой переменной и остатками регрессии (вертикальное расстояние между построенной точкой и подобранной линией регрессии).

Иллюстрация 9 показывает значения зависимых и независимых переменных и установленную линию регрессии для модели с гетероскедастическими ошибками.

Здесь систематическая связь визуально очевидна: в среднем остатки регрессии растут намного больше, по мере роста значения независимой переменной.

Последствия гетероскедастичности.

Каковы последствия нарушения допущения о постоянной дисперсии ошибок?

Хотя гетероскедастичность не влияет на согласованность (Greene 2018) параметров регрессии, она может привести к ошибкам в статистическом выводе.

Неформально, оценка параметра регрессии является согласованной, если вероятность того, что оценка параметра регрессии отличается от истинного значения параметра уменьшается при увеличении количества наблюдений, используемых в регрессии.

Когда ошибки являются гетероскедастическими, F-тест (F-критерий) для общей значимости регрессии является ненадежным. Эта ненадежность вызвана тем, что средняя квадратная ошибка является смещенной оценкой истинной дисперсии совокупности с учетом гетероскедастичности.

Кроме того, t-тесты (t-критерии) для оценки значимости отдельных коэффициентов регрессии также ненадежны, поскольку гетероскедастичность приводит к смещению оценки стандартной ошибки коэффициентов регрессии.

Если регрессия показывает значительную гетероскедастичность, стандартные ошибки и статистики тестов, рассчитанные с помощью статистического ПО, будут неверны, если не будут скорректированы с поправкой на гетероскедастичность.

Иллюстрация 8. Регрессия с гомоседастичностью.

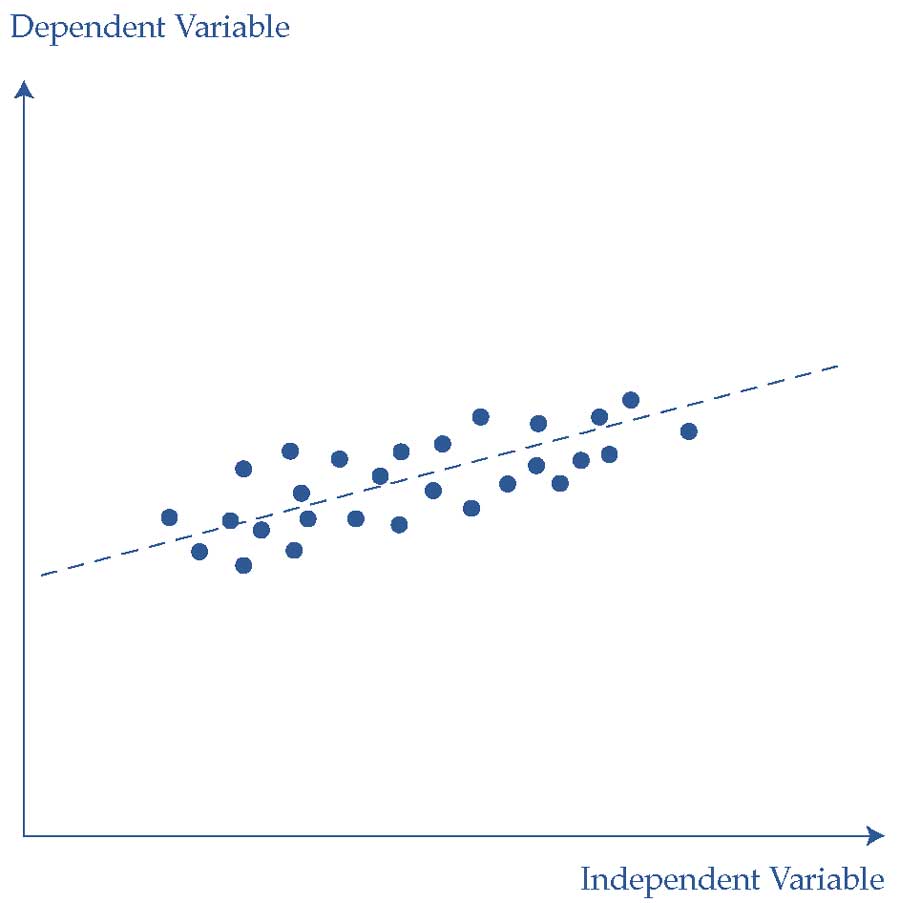
Иллюстрация 8. Регрессия с гомоседастичностью.

Иллюстрация 9. Регрессия с гетероскедастичностью.

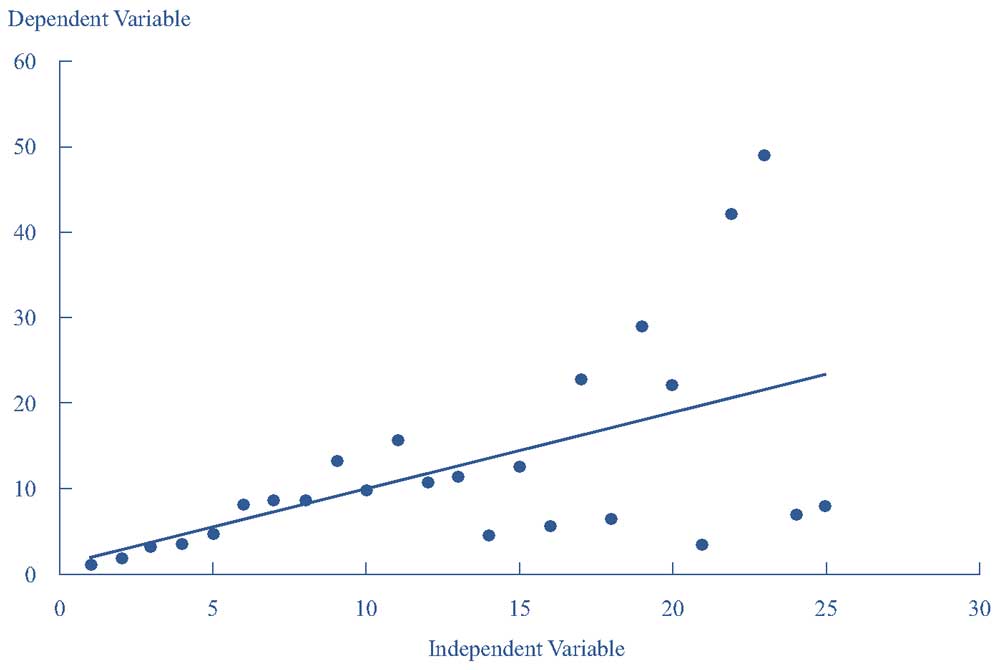
Иллюстрация 9. Регрессия с гетероскедастичностью.

В регрессиях с финансовыми данными наиболее вероятным результатом гетероскедастичности является то, что стандартные ошибки будут недооценены, а F-статистики будут завышены.

Когда мы игнорируем гетероскедастичность, мы склонны находить значимые взаимосвязи, которые на самом деле не существуют.

Однако, иногда неспособность корректировать гетероскедастичность приводит к слишком большим стандартным ошибкам (и слишком малым t-статистикам). На практике, последствия этого могут быть серьезными, если мы используем регрессионный анализ в разработке инвестиционных стратегий.

Как показано в Иллюстрации 10, эта проблема вредит нашему пониманию финансовых моделей.

Иллюстрация 10. Гетероскедастичность и тестирование модели ценообразования активов.

MacKinlay и Richardson (1991) изучили, как гетероскедастичность влияет на тесты модели оценки капитальных активов (CAPM). Эти авторы утверждают, что если модель CAPM верна, то нет существенных различий между доходностью с поправкой на риск для малых объемов акций по сравнению с большими объемами.

Чтобы проверить это, MacKinlay и Richardson, сгруппировали все акции Нью-Йоркской фондовой биржи и Американской фондовой биржи (NYSE MKT) по рыночной стоимости.

Затем они протестировали систематические различия в доходности с поправкой на риск среди портфелей акций, сформированных на основе рыночной капитализации. Они оценили следующую регрессию:

\( r_{i,t} = \alpha_i + \beta_i r_{m,t} + \epsilon_{i,t} \),

где

Формулировка CAPM предполагает, что избыточная доходность портфеля объясняется избыточной доходностью на рынке в целом.

Эта гипотеза подразумевает, что \( \alpha_i = 0 \) для каждого портфеля \( \i \); в среднем, избыточная доходность отсутствует в любом портфеле после учета его систематического (рыночного) риска.

Используя данные с января 1926 года по декабрь 1988 года и рыночный индекс, основанный на равновзвешенной доходности, MacKinlay и Richardson не смогли отклонить CAPM на уровне значимости 0.05, когда они делали допущение, что ошибки в модели регрессии нормально распределены и гомоскедастичны.

Однако они обнаружили, что могут отклонить CAPM, когда исправили свои статистики тестирования, чтобы учесть гетероскедастичность. Они отклонили гипотезу о том, что в исторических данных нет избыточной доходности.

---

Мы заявили, что влияние гетероскедастичности на статистический вывод может быть серьезным. Чтобы быть более точным в этой концепции, мы должны различать два широких вида гетероскедастичности: безусловную и условную.

Безусловная гетероскедастичность (англ. 'unconditional heteroskedasticity') возникает, когда гетероскедастичность дисперсии ошибок не коррелирует с независимыми переменными в множественной регрессии. Хотя эта форма гетероскедастичности нарушает Допущение 4 модели линейной регрессии, она не создает серьезных проблем для статистического вывода.

Тип гетероскедастичности, который вызывает наибольшие проблемы для статистического вывода - условная гетероскедастичность (англ. 'unconditional heteroskedasticity'). Это гетероскедастичность в дисперсии ошибок, которая в зависимости от условий коррелирует со значениями независимых переменных в регрессии.

К счастью, многие статистические программные пакеты легко проверяют и корректируют условную гетероскедастичность.

 

Проверка на гетероскедастичность.

Из-за последствий условной гетероскедастичности для статистического вывода аналитик должен иметь возможность диагностировать ее присутствие. Тест (критерий) Бреуша-Пагана (англ. 'Breusch-Pagan test') широко используется в финансовых исследованиях из-за его общности.

Breusch и Pagan (1979) предложили следующий тест на условную гетероскедастичность: регрессировать квадратные остатки из уравнения регрессии по независимым переменным в регрессии.

Если условной гетероскедастичности не существует, независимые переменные не будут объяснять большую часть вариации в квадратных остатках. Однако, если в исходной регрессии присутствует условная гетероскедастичность, независимые переменные объяснят значительную часть вариации в квадратных остатках.

Независимые переменные могут объяснить вариацию, поскольку квадратный остаток каждого наблюдения будет коррелировать с независимыми переменными, если независимые переменные влияют на дисперсию ошибок.

Breusch и Pagan показали, что при нулевой гипотезе об отсутствии условной гетероскедастичности \(nR^2\) (из регрессии квадратных остатков по независимым переменным исходной регрессии) будет случайной переменной \(\chi^2\) с количеством степеней свободы равным количеству независимых переменных в регрессии (для получения дополнительной информации о критерии Бреуша-Пагана, см. Greene 2018).

Следовательно, нулевая гипотеза гласит, что квадратная ошибка уравнения регрессии не коррелирует с независимыми переменными. Альтернативная гипотеза утверждает, что квадратная ошибка коррелирует с независимыми переменными. Иллюстрация 11 демонстрирует критерий Бреуша-Пагана для условной гетероскедастичности.

Иллюстрация 11. Проверка на условную гетероскедастичность во взаимосвязи между процентными ставками и ожидаемой инфляцией.

Предположим, что аналитик хочет выяснить, насколько тесно номинальные процентные ставки связаны с ожидаемой инфляцией, чтобы определить, как распределить активы в портфеле ценных бумаг с фиксированным доходом.

Аналитик хочет проверить эффект Фишера. Гипотеза, предложенная Ирвингом Фишером, заключается в том, что номинальные процентные ставки увеличиваются на 1 процентный пункт на каждое увеличение ожидаемой инфляции на 1%.

Эффект Фишера предполагает следующую связь между номинальными процентными ставками, реальными процентными ставками и ожидаемой инфляцией:

\( i = r + \pi^e \),

где

Чтобы проверить эффект Фишера, используя данные временных рядов, мы могли бы построить следующую регрессионную модель для номинальной процентной ставки:

\( i_t = b_0 + b_1 \pi^e_t + \epsilon_t \) (8)

Учитывая, что эффект Фишера предсказывает, что коэффициент переменной инфляции составляет 1, мы можем изложить нулевые и альтернативные гипотезы следующим образом:

Мы также могли бы установить уровень значимости 0,05 для этого теста. Прежде чем мы оценим Уравнение 8, мы должны решить, как измерить ожидаемую инфляцию (\( \pi^e_t \)) и номинальную процентную ставку (\( i_t \)).

Исследование профессиональных прогнозистов (SPF) включает данные о квартальных инфляционных ожиданиях профессиональных прогнозистов с использованием годового медианного прогноза SPF роста дефлятора ВВП в текущем квартале.

Мы используем эти данные в качестве нашей меры ожидаемой инфляции. Мы используем трехмесячную доходность казначейских облигаций США в качестве эквивалента (безрисковой) номинальной процентной ставки.

Мы используем ежеквартальные данные с четвертого квартала 1968 года по четвертый квартал 2013 года для оценки регрессии по Уравнению 8. Результаты расчета показаны далее.

Чтобы принять статистическое решение о том, поддерживают ли данные эффект Фишера, мы рассчитываем следующую t-статистику, которую затем сравниваем с ее критическим значением:

\( \dst t = {\hat b_1 - b_1 \over s_{\hat b_1}} = {1.1744-1 \over 0.0761} = 2.29 \).

При уровне значимости 0.05 и \(181 - 2 = 179\) степенях свободы критическое t-значение составляет около 1.97.

Если мы выполнили обоснованный тест, мы можем отклонить на уровне значимости 0.05 гипотезу о том, что истинный коэффициент в этой регрессии составляет 1 и что эффект Фишера сохраняется.

t-тест (t-критерий) предполагает, что ошибки гомоскедастические. Прежде чем мы примем обоснованность t-критерия, мы должны проверить, являются ли ошибки условно гетероскедастическими. Если эти ошибки оказываются условно гетероскедастическими, то тест необоснован.

 

Результаты регрессии доходности казначейских облигаций по прогнозируемой инфляции.

	Коэффициент	Стандартная ошибка	t-статистика
Точка пересечения	0.0116	0.0033	3.5152
Прогнозируемая инфляция	1.1744	0.0761	15.4323
Стандартная ошибка остатка	0.0233
Множественный \( R^2 \)	0.5708
Наблюдения	181
Статистика Дурбина-Уотсона	0.2980

---

Мы можем выполнить тест (критерий) Бреуша-Пагана на условную гетероскедастичность для квадратных остатков из регрессии эффекта Фишера.

Тест регрессирует квадратные остатки по прогнозируемому уровню инфляции. \(R^2\) в регрессии квадратных остатков (здесь не показан) составляет 0.0666.

Статистика теста из этой регрессии, \(nR^2\), составляет \( 181 \times 0.0666 = 12.0546 \).

В соответствии с нулевой гипотезой об отсутствии условной гетероскедастичности эта статистика представляет собой случайную переменную \(\chi^2\) с одной степенью свободы (поскольку существует только одна независимая переменная).

Мы должны быть обеспокоены гетероскедастичностью только при больших значениях статистики теста. Поэтому мы должны использовать односторонний тест, чтобы определить, можем ли мы отклонить нулевую гипотезу.

Критическое значение статистики для переменной из распределения \(\chi^2\) с одной степенью свободы на уровне значимости 0.05 составляет 3.84.

Статистика из теста Бреушу-Пагана составляет 12.0546, поэтому мы можем отклонить гипотезу о безусловной гетероскедастичности на уровне значимости 0.05.

Фактически, мы даже можем отвергнуть гипотезу об отсутствии условной гетероскедастичности на уровне значимости 0.01, поскольку критическое значение статистики в этом случае составляет 6.63.

В результате мы заключаем, что ошибка в регрессии эффекта Фишера является условно гетероскедастической.

Стандартные ошибки, рассчитанные в исходной регрессии, не верны, поскольку они не учитывают гетероскедастичность. Поэтому мы не можем принять t-тест как обоснованный.

В Иллюстрации 11 мы пришли к выводу, что t-критерий, который мы могли бы использовать для проверки эффекта Фишера, не был обоснованным.

Означает ли это, что мы не можем использовать регрессионную модель для исследования эффекта Фишера?

К счастью, нет. Существует методология для корректировки стандартной ошибки коэффициентов регрессии, позволяющая исправить гетероскедастичность.

Используя скорректированную стандартную ошибку для \( \hat b_1 \), мы можем повторно проверить t-критерий. Как мы увидим в следующем разделе, используя этот обоснованный t-критерий, мы не будем отклонять нулевую гипотезу из Иллюстрации 11.

То есть, наш статистический вывод изменится после того, как мы сделаем поправку на гетероскедастичность.

 

Поправка на гетероскедастичность.

Финансовые аналитики должны знать, как исправить гетероскедастичность, потому что такая коррекция может изменить выводы о проверке конкретной гипотезы и, таким образом, повлиять на конкретное инвестиционное решение.

Например, в Иллюстрации 10 MacKinlay и Richardson изменили свои инвестиционные выводы после корректировки тестов значимости их модели с учетом гетероскедастичности.

Мы можем использовать два разных метода для исправления эффектов условной гетероскедастичности в моделях линейной регрессии.

Первый метод, вычисляющий надежные стандартные ошибки, исправляет стандартные ошибки коэффициентов модели линейной регрессии для учета условной гетероскедастичности.

Второй метод, известный как обобщенный метод наименьших квадратов (англ. 'generalized least squares'), изменяет исходное уравнение, чтобы устранить гетероскедастичность. Затем новое модифицированное уравнение регрессии оценивается с учетом допущения о том, что гетероскедастичность больше не является проблемой.

Технические детали, стоящие за этими двумя методами корректировки условной гетероскедастичности выходят за рамки данного обсуждения.

Однако многие статистические программные пакеты могут легко вычислять надежные стандартные ошибки, и мы рекомендуем использовать их. Обратите внимание, что надежные стандартные ошибки также известны как гетероскедастически согласованные стандартные ошибки (heteroskedasticity-consistent standard errors, White-corrected standard errors).

Возвращаясь к теме Иллюстрации 11, касающейся эффекта Фишера, напомним, что мы пришли к выводу, что дисперсия ошибки была гетероскедастической.

Если мы исправим стандартные ошибки коэффициентов регрессии для корректировки условной гетероскедастичности, мы получим результаты, показанные в Иллюстрации 12.

Сравнивая стандартные ошибки с Иллюстрацией 11, мы видим, что стандартная ошибка для точки пересечения почти не изменилась, но стандартная ошибка для коэффициента прогнозируемой инфляции (коэффициент наклона) увеличивается примерно на 22% (с 0.0761 до 0.0931).

Также обратите внимание, что коэффициенты регрессии одинаковы в обеих таблицах, потому что результаты корректируют только стандартные ошибки из Иллюстрации 11.

Иллюстрация 12. Результаты регрессии доходности казначейских облигаций по прогнозируемой инфляции (стандартные ошибки, скорректированные на условную гетероскедастичность).

	Коэффициент	Стандартная ошибка	t-статистика
Точка пересечения	0.0116	0.0034	3.4118
Прогнозируемая инфляция	1.1744	0.0931	12.6144
Стандартная ошибка остатка	0.0233
Множественный \( R^2 \)	0.5708
Наблюдения	181

Теперь мы можем выполнить обоснованный t-критерий нулевой гипотезы о том, что коэффициент наклона имеет истинное значение 1, используя надежную стандартную ошибку для \( \hat b_1 \).

Мы находим, что:

\( \dst t = {1.1744 - 1 \over 0.0931} = 1.8733 \).

Этот результат меньше критического значения 1.97, необходимого для отклонения нулевой гипотезы о том, что наклон равен 1 (помните, что это двусторонний тест).

Таким образом, мы больше не можем отвергать нулевую гипотезу о том, что наклон равен 1 из-за большей неопределенности (стандартная ошибка), связанной с оценкой коэффициента.

Таким образом, в этом примере корректировка на статистически значимую условную гетероскедастичность оказала влияние на результат проверки гипотезы о наклоне коэффициента прогнозируемой инфляции.

Иллюстрация 10, касающаяся тестов CAPM, является аналогичным случаем. В других случаях, однако, наше статистическое решение может остаться неизменным при использовании надежных стандартных ошибок в t-критерии.