Более распространенной и потенциально более серьезной проблемой, чем нарушение допущения о гомоскедастичности, является нарушение допущения о том, что ошибки регрессии не коррелируют для разных наблюдений.

Попытка объяснить конкретные финансовые взаимосвязи в течение ряда периодов рискованна, потому что ошибки в моделях финансовой регрессии часто коррелируют во времени.

Когда ошибки регрессии коррелируют между наблюдениями, мы говорим, что они сериально коррелируют (или автокоррелируют). Сериальная корреляция (англ. 'serial correlation') наиболее часто возникает в регрессиях временных рядов.

В этом разделе мы обсуждаем три аспекта сериальной корреляции: ее влияние на статистический вывод, проверка на ее возникновение и методы ее исправления.

Последствия сериальной корреляции.

Как и в случае с гетероскедастичностью, основная проблема, вызванная сериальной корреляцией в линейной регрессии, представляет собой неверную оценку стандартных ошибок регрессии, вычисленных статистическими программными пакетами.

Пока ни одна из независимых переменных не является запаздывающим значением зависимой переменной (т.е. значением зависимой переменной из предыдущего периода), сами по себе оценочные параметры будут согласованы и не должны быть скорректированы для устранения воздействия сериальной корреляции.

Если, однако, одна из независимых переменных является запаздывающим значением зависимой переменной (например, если доходность облигации за предыдущий месяц была независимой переменной в регрессии эффекта Фишера), автокорреляция ошибки приведет к тому, все оценочные параметры линейной регрессии будут несоответствующими и недопустимыми оценками истинных значений параметров (мы рассмотрим это позже).

Ни в одной из рассмотренных нами регрессий не было независимой переменной, являющейся запаздывающим значением зависимой переменной. Таким образом, в этих регрессиях эффект сериальной корреляции появляется в стандартных ошибках коэффициента регрессии.

Здесь мы рассмотрим случай положительной автокорреляции, потому что он наиболее распространен. Положительной сериальной корреляцией (англ. 'positive serial correlation') является сериальная корреляция, в которой положительная ошибка для одного наблюдения увеличивает вероятность положительной ошибки для другого наблюдения.

Положительная автокорреляция также означает, что отрицательная ошибка для одного наблюдения увеличивает вероятность отрицательной ошибки для другого наблюдения.

Напротив, при отрицательной сериальной корреляции (англ. 'negative serial correlation') положительная ошибка для одного наблюдения увеличивает вероятность отрицательной ошибки для другого наблюдения, а отрицательная ошибка для одного наблюдения увеличивает вероятность положительной ошибки для другого.

При изучении положительной автокорреляции мы делаем общее допущение о том, что сериальная корреляция принимает форму сериальной корреляции первого порядка или автокорреляции между соседними наблюдениями.

В контексте временных рядов это допущение означает, что знак ошибки имеет тенденцию сохраняться от одного периода к другому.

Хотя положительная автокорреляция не влияет на согласованность коэффициентов регрессии, она влияет на нашу способность выполнять достоверные статистические тесты.

Во-первых, F-статистика для проверки на общей значимости регрессии может быть завышена, поскольку средняя квадратная ошибка (MSE, mean squared error) будет иметь тенденцию недооценивать дисперсию ошибок совокупности.

Во-вторых, положительная автокорреляция обычно приводит к тому, что стандартные ошибки коэффициентов регрессии, рассчитанные методом наименьших квадратов (OLS, ordinary least squares), недооценивают истинные стандартные ошибки.

Следовательно, если в регрессии присутствует положительная автокорреляция, стандартный линейный регрессионный анализ обычно приводит нас к вычислению искусственно заниженных стандартных ошибок для коэффициентов регрессии.

Эти небольшие стандартные ошибки приводят к завышению оцениваемой t-статистики, что предполагает значимость там, где ее, возможно, нет.

Завышенная t-статистика, в свою очередь, может привести к тому, что мы будем чаще ошибочно отклонять нулевые гипотезы о значениях совокупности для параметров регрессии, чем при правильно оцененных стандартных ошибках.

Эта ошибка I рода может привести к неправильным инвестиционным рекомендациям.

Тестирование на сериальную корреляцию.

Мы можем выбирать из множества тестов на наличие сериальной корреляции в регрессионной модели (см. Greene 2018), но наиболее распространенным методом является статистика, разработанная Дурбином и Уотсоном (1951).

Фактически, многие статистические программные пакеты автоматически вычисляют статистику Дурбина-Уотсона (англ. 'Durbin-Watson statistic').

Уравнение для расчета статистики теста (критерия) Дурбина-Ватсона (англ. 'Durbin-Watson test'):

\( \dst
{\rm DW} = { \dst \sum^T_{t=2} \left( \hat \epsilon_t - \hat \epsilon_{t-1} \right)^2
\over  \dst \sum^T_{t=1} \hat \epsilon_t^2 }
\) (9)

где \( \hat \epsilon_t \) является остатком регрессии для периода \(t\). Мы можем преобразовать это уравнение следующим образом:

\( \dst
{ \dst {1 \over T-1} \sum^T_{t=2} \left( \hat \epsilon_t^2 -
2\hat \epsilon_t  \hat \epsilon_{t-1}
+ \hat \epsilon_{t-1}^2 \right)
\over  \dst {1 \over T-1} \sum^T_{t=1} \hat \epsilon_t^2 } \approx
\)

\( \dst   {
{\rm Var}( \hat \epsilon_t ) -
2 {\rm Cov}( \hat \epsilon_t , \hat \epsilon_{t-1} ) +
{\rm Var}( \hat \epsilon_{t-1} ) \over
{\rm Var}( \hat \epsilon_t )
} \)

Если дисперсия ошибки постоянна во времени, то мы ожидаем, что \( {\rm Var}( \hat \epsilon_t ) = \hat \sigma^2_{\epsilon} \) для всех \(t\), где мы используем \( \sigma^2_{\epsilon} \) для представления постоянной дисперсии ошибки.

Если ошибки также не имеют автокорреляции, то мы ожидаем, что:

\( \dst {\rm Cov}( \hat \epsilon_t , \hat \epsilon_{t-1} ) = 0 \).

В этом случае статистика Дурбина-Уотсона приблизительно равна:

\( \dst
{ \hat \sigma_{\epsilon}^2 - 0 + \hat \sigma_{\epsilon}^2
\over \hat \sigma_{\epsilon}^2 } = 2
\)

Это уравнение говорит нам о том, что если ошибки гомоскедастические и не имеют сериальной корреляции, то статистика Дурбина-Уотсона будет близка к 2.

Следовательно, мы можем проверить нулевую гипотезу о том, что ошибки не имеют сериальной корреляции, с помощью тестирования на то, насколько значительно статистика Дурбина-Уотсона отличается от 2.

Если выборка очень большая, статистика Дурбина-Уотсона будет приблизительно равна \(2(1 - r)\), где \(r\) - это корреляция между остатками регрессии из одного периода и из предыдущего периода.

Это приближение полезно, потому что оно показывает значение статистики Дурбин-Уотсона для различных уровней сериальной корреляции.

Статистика Дурбина-Уотсона может принимать значения от 0 (при сериальной корреляции +1) до 4 (при сериальной корреляции -1):

  • Если регрессия не имеет сериальной корреляции, то остатки регрессии не будут коррелировать во времени, а значение статистики Дурбина-Уотсона будет равно \(2(1 - 0) = 2\).
  • Если остатки регрессии положительно сериально коррелируют, то статистика Дурбина-Уотсона будет составлять менее 2. Например, если сериальная корреляция ошибок составляет 1, то значение статистики Дурбина-Уотсон будет равно 0.
  • Если остатки регрессии отрицательно коррелируют, то статистика Дурбина-Уотсона будет больше 2. Например, если сериальная корреляция ошибок составляет -1, то значение статистики Дурбина-Уотсона будет равно 4.

Возвращаясь к Иллюстрации 11, в которой исследуется эффект Фишера, статистика Дурбина-Уотсона для регрессии OLS составляет 0.2980.

Этот результат означает, что остатки регрессии положительно сериально коррелируют:

\( \begin{aligned}
{\rm DW} &= 0.2980 \\ &\approx 2(1-r) \\
r &\approx 1 - {\rm DW}/2 \\
&= 1-0.2980/2 \\ &= 0.8510
\end{aligned} \)

Этот результат вызывает обеспокоенность тем, что стандартные ошибки, рассчитанные методом наименьших квадратов (OLS) могут быть неверными из-за положительной сериальной корреляции.

Предоставляет ли наблюдаемая статистика Дурбина-Уотсона (0.2980) достаточно доказательств, чтобы гарантировать отклонение нулевой гипотезы об отсутствии положительной сериальной корреляции?

Мы должны отклонить нулевую гипотезу об отсутствии сериальной корреляции, если статистика Дурбина-Уотсона ниже критического значения \(d*\). К сожалению, Дурбин и Уотсон также установили, что для данной выборки мы не можем знать истинное критическое значение, \(d*\).

Вместо этого мы можем определить только то, что \(d*\) лежит либо между двумя значениями, \(d_u\) (верхний предел) и \(d_l\) (нижний предел), либо за пределами этих значений.

Иллюстрация 13 изображает верхние и нижние пределы \(d*\) результатов статистики Дурбина-Уотсона.

Иллюстрация 13. Значения статистики Дурбина-Уотсона.

Иллюстрация 13. Значения статистики Дурбина-Уотсона.
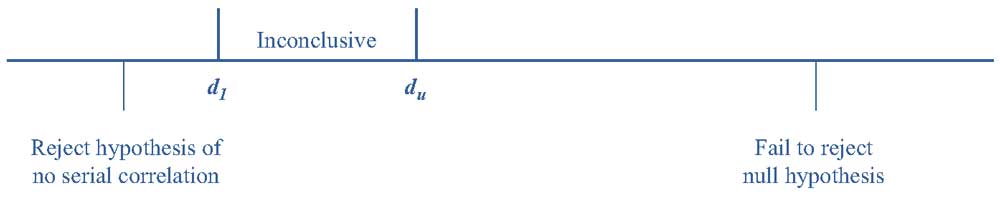
Иллюстрация 13. Значения статистики Дурбина-Уотсона.

Из Иллюстрации 13 мы узнаем следующее:

  • Когда статистика Дурбина-Ватсона (DW) меньше \(d_l\), мы отвергаем нулевую гипотезу от отсутствии положительной автокорреляции.
  • Когда статистика DW находится в промежутке между \(d_l\) и \(d_u\), результаты теста неубедительны.
  • Когда статистика DW больше, чем \(d_u\), мы не можем отклонить нулевую гипотезу об отсутствии положительной автокорреляции (иногда автокорреляция в регрессионной модели является отрицательной, а не положительной).
    Для нулевой гипотезы об отсутствии автокорреляции нулевая гипотеза отвергается, если \( {\rm DW} < d_l \), что указывает на значительную положительную автокорреляцию; или если \( {\rm DW} > 4 - d_l \), что указывает на значительную отрицательную автокорреляцию.

Возвращаясь к Иллюстрации 11, регрессия эффекта Фишера имеет одну независимую переменную и 181 наблюдение. Статистика Дурбина-Уотсона составляет 0.2980.

Мы можем отвергнуть нулевую гипотезу об отсутствии корреляции в пользу альтернативной гипотезы о положительной автокорреляции на уровне 0.05, поскольку статистика Дурбина-Уотсона намного ниже \(d_l\) при \(k = 1\) и \(n = 100 (1.65)\).

Уровень \(d_l\) будет даже выше для выборки из 181 наблюдения. Такая значительная положительная сериальная корреляции предполагает, что стандартные ошибки OLS (рассчитанные методом наименьших квадратов) в этой регрессии, вероятно, значительно недооценивают истинные стандартные ошибки.

Корректировка сериальной корреляции.

У нас есть два альтернативных способа по исправлению положения, когда регрессия имеет значительную сериальную корреляцию.

Во-первых, мы можем скорректировать стандартные ошибки коэффициента так, чтобы параметры линейной регрессии учитывали сериальную корреляцию.

Во-вторых, мы можем изменить само уравнение регрессии, чтобы устранить сериальную корреляцию. Мы рекомендуем использовать первый метод; второй метод может привести к необоснованным оценкам параметров, если не проявлять чрезвычайную осторожность.

Два наиболее распространенных метода корректировки стандартных ошибок были разработаны Хансеном (1982), Ньюи и Вестом (1987).

Эти методы являются стандартным функционалом во многих статистических программных пакетах, а сама корректировка известна под различными названиями: serial-correlation consistent standard errors, serial correlation and heteroskedasticity adjusted standard errors, robust standard errors.

Дополнительным преимуществом этих методов является то, что они также исправляют условную гетероскедастичность.

В Иллюстрации 14 показаны результаты исправления стандартных ошибок из Иллюстрации 11 для сериальной корреляции и гетероскедастичности с использованием метода Ньюи-Веста.

Обратите внимание, что коэффициенты как для точки пересечения, так и для наклона такие же, как и в исходной регрессии. Однако надежные стандартные ошибки стали намного больше - более чем вдвое больше стандартных ошибок OLS из Иллюстрации 11.

Из-за серьезной сериальной корреляции в ошибке регрессии, метод наименьших квадратов (OLS) сильно недооценивает неопределенность в отношении предполагаемых параметров регрессии.

Также обратите внимание, что сериальная корреляция не была устранена, но стандартная ошибка была скорректирована ​​для учета сериальной корреляции.

Иллюстрация 14. Результаты регрессии доходности казначейских облигаций по прогнозируемой инфляции (стандартные ошибки, скорректированные с учетом условной гетероскедастичности и сериальной корреляции).

Коэффициент

Стандартная ошибка

t-статистика

Точка пересечения

0.0116

0.0067

1.7313

Прогнозируемая инфляция

1.1744

0.1751

6.7070

Стандартная ошибка остатка

0.0233

Множественный \(R^2\)

0.5708

Наблюдения

181

Теперь предположим, что мы хотим проверить нашу первоначальную нулевую гипотезу (эффект Фишера) о том, что коэффициент по прогнозируемой инфляции равен 1 (\(H_0: b_1 = 1\)) против альтернативной гипотезы о том, что коэффициент не равен 1 (\(H_a: b_1 \neq 1\)).

При скорректированных стандартных ошибках значение статистики теста для этой нулевой гипотезы составит:

\( \dst
{\hat b_1 - b_1 \over s_{\hat b_1} } =
{ 1.1744-1 \over 0.1751} = 0.996
\)

Критические значения как для уровня значимости 0.05, так и для 0.01, намного больше, чем 0.996 (статистика t-критерия), поэтому мы не можем отклонить нулевую гипотезу.

Этот вывод такой же, как и в Иллюстрации 10, где корректировка выполнялась только для гетероскедастичности.

Это показывает, что для некоторых гипотез сериальная корреляция и условная гетероскедастичность могут оказать большое влияние на то, принимаем ли мы или отвергаем эти гипотезы. Кроме того, сериальная корреляция также может повлиять на точность прогноза.