CFA - Множественная линейная регрессия с качественными зависимыми переменными

Качественные зависимые переменные (англ. 'qualitative dependent variables'), которые также называют градационными зависимыми переменными (англ. 'categorical dependent variables'), являются переменными классификации результата регрессии, которые описывают данные, относящиеся к определенным категориям.

Например, чтобы предсказать, станет ли компания банкротом, нам необходимо использовать качественную зависимую переменную (банкрот или нет) в качестве зависимой переменной и использовать данные о финансовой устойчивости компании (например, рентабельность собственного капитала, коэффициент финансового левериджа или кредитный рейтинг) в качестве независимых переменных.

В этом примере качественная зависимая переменная является бинарной переменной. Это один из многих потенциальных сценариев, в которых финансовые аналитики должны иметь возможность объяснить результаты качественной зависимой переменной, которая описывает данные, принадлежащие двум категориям.

Также можно провести анализ, где зависимая переменная делится не более чем две категории.

Например, рейтинг Moody's Bank Financial Strength Rating - это качественная переменная, которая указывает на рейтинг или категорию Moody's (A, B, C, D или E) для банка.

В отличие от линейной регрессии, зависимая переменная здесь не носит непрерывный характер, но является дискретной и в простом сценарии имеет две категории. К сожалению, для оценки такой модели линейная регрессия является не лучшим статистическим методом.

Если мы используем качественную зависимую переменную

Y = {банкрот (= 1) или не банкрот (= 0)}

в регрессии с финансовыми переменными в качестве независимых переменных, то мы получим модель линейной вероятности:

\( l_i = b_0 + b_1 X_{1i} + b_2 X_{2i} + b_3 X_{3i} + \epsilon_i  \), (13)

К сожалению, прогнозируемое значение зависимой переменной может быть намного больше, чем на 1 или намного меньше, чем 0, в зависимости от коэффициентов \(b_i\) и значений наблюдаемых переменных \(X_i\).

Конечно, эти результаты будут недействительными. Вероятность банкротства не может превышать 1.0 или быть ниже 0.

Другая проблема с использованием линейной регрессии заключается в том, что связь между вероятностью банкротства и каждой финансовой переменной будет линейной для всего диапазона финансовых переменных.

Однако мы можем не ожидать этого. Например, мы можем ожидать, что вероятность банкротства и коэффициент финансового левериджа (т.е. отношение долга к собственному капиталу) не связаны линейно при очень низком или очень высоком уровне отношения долга к собственному капиталу.

Чтобы решить эти проблемы с линейностью, мы должны выполнить нелинейное преобразование в вероятность банкротства и линейно связать преобразованную вероятность с независимыми переменными.

Есть много возможных преобразований, которые тесно связаны, за исключением случаев, когда вероятность слишком низкая или высокая.

Наиболее часто используемым преобразованием является логистическое преобразование (англ. 'logistic transformation').

В этом преобразовании «\(p\)» обозначает вероятность того, что компания обанкротится, или в более широком смысле, выполнение условия или возникновение события.

Логистическое преобразование имеет следующий вид:

\( \ln \left(\dst{p \over 1-p}  \right) \).

Коэффициент \( \left(\dst{p \over 1-p} \right) \) это отношение вероятностей - вероятность того, что интересующее событие произойдет (\(p\)), деленная на вероятность того, что оно не произойдет (\(1-p\)) Это соотношение называют шансами возникновения события.

Например, если вероятность банкротства компании составляет 0.75, то коэффициент \( \left(\dst{p \over 1-p} \right) \) будет равен:

\( 0.75/(1 - 0.75) = 0.75/0.25 = 3 \).

Таким образом, шансы банкротства составляют 3, что указывает на то, что вероятность банкротства в три раза больше, чем вероятность того, что компания не обанкротится. Натуральный логарифм шансов на возникновение события называют логарифмом отношения шансов (англ. 'log odds') или логит-преобразованием (англ. 'logit').

Логистическое преобразование имеет тенденцию делать линейной связь между зависимыми и независимыми переменными.

Для оценки вероятности банкротства вместо линейной регрессии мы должны использовать логистическую регрессию (англ. 'logistic regression'), также известную как логит-модель (англ. 'logit model') или дискриминантный анализ (англ. 'discriminant analysis').

Модели логистической регрессии используются для оценки вероятности дискретного результата, с учетом значений независимых переменных, используемых для объяснения этого результата.

Логистическая регрессия широко используется в машинном обучении, где целью является классификация. Логистическая регрессия включает в себя использование логистического преобразования вероятности события в качестве зависимой переменной:

\( \ln \left(\dst{p \over 1-p} \right) =
b_0 + b_1 X_1 + b_2 X_2 + b_3 X_3 + \epsilon \). (14)

Вероятность события можно получить из Формулы 14:

\( \dst p = { 1 \over
1 + \exp \Bigl [ - \left( b_0 + b_1 X_1 + b_2 X_2 + b_3 X_3
+ \right) \Bigr ] } \). (15)

Иллюстрация 25. Линейные модели вероятности в сравнении с логит-моделями.

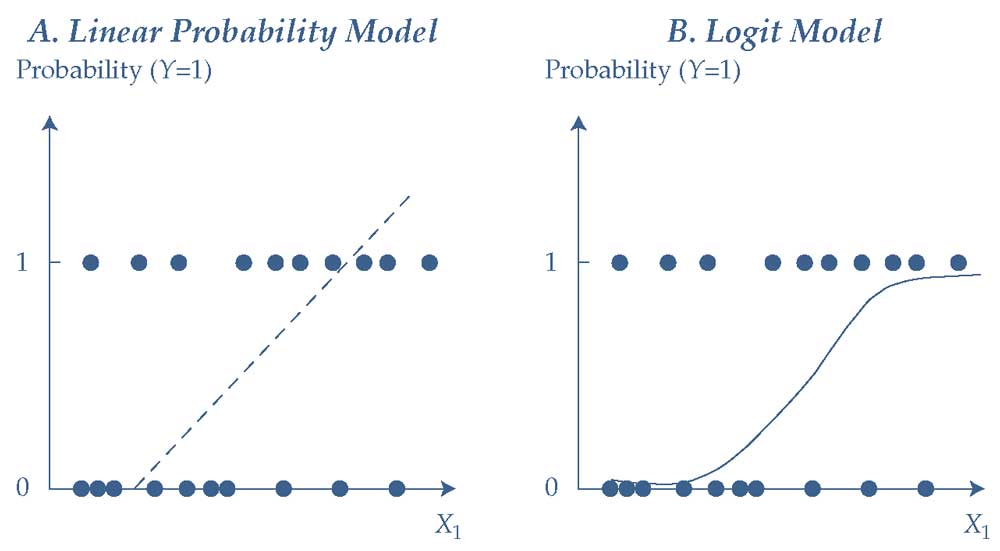
Линейные модели вероятности в сравнении с логит-моделями.

Эта нелинейная функция принимает сигмоидальную форму (т.е. S-образную), показанную в Иллюстрации 25. Форма приблизительно линейна, за исключением случаев, когда оценки вероятности близки к 0 или 1.

Можно заметить, что нелинейное преобразование ограничивает оценки вероятности в диапазоне от 0 до 1. Мы также можем увидеть это математически.

 

По мере того, как \((b_0 + b_1 X_1 + b_2 X_2 + b_3 X_3)\) стремится к положительной бесконечности, \(p\) стремится к 1; и по мере того, как \((b_0 + b_1 X_1 + b_2 X_2 + b_3 X_3)\) стремится к отрицательной бесконечности, \(p\) стремится к 0.

Логистическая регрессия предполагает логистическое распределение для члена ошибки; это распределение имеет одинаковую форму с нормальным распределением, но имеет более тяжелые хвосты.

Для бинарного \(p\) \( \ln \left(\dst{p \over 1-p} \right) \) не определен как при \(p=0\), так и при \(p=1\). В этом случае коэффициенты логистической регрессии нужно оценивать скорее с помощью метода максимального правдоподобия, чем методом наименьших квадратов.

Метод максимального правдоподобия (англ. 'maximum likelihood method') оценивает коэффициенты логистической регрессии путем максимизации функции правдоподобия для данных.

Мы должны сделать предположение о распределении вероятностей \(p\), чтобы построить функцию правдоподобия. Поскольку \(p\) бинарна, следует выбрать распределение Бернулли в качестве распределения вероятности.

Метод максимального правдоподобия - это итеративный метод, цель которого - максимизировать логарифмическое правдоподобие.

Каждая итерация приводит к более высокому логарифмическому правдоподобию, и процесс итерации останавливается, когда разница в логарифмическом правдоподобии двух успешных итераций оказывается довольно мала.

Поскольку логит-модель имеет логистическое преобразование вероятности события в качестве зависимой переменной, интерпретация коэффициентов регрессии не так проста или интуитивна, как для обычной линейной регрессии.

В линейной регрессии коэффициентом наклона независимой переменной является изменение зависимой переменной на 1 единицу изменения в независимой переменной, при неизменных всех прочих независимых переменных.

В логит-модели коэффициент наклона - это изменение «логарифма отношения шансов» на то, что событие произойдет при изменении на 1 единицу независимой переменной, при неизменных всех прочих независимых переменных.

Экспонентой коэффициента наклона является «отношение шансов», которое является отношением шансов на то, что событие произойдет при увеличении на 1 единицу независимой переменной, к вероятности того, что событие произойдет без увеличения независимой переменной.

Проверка гипотезы о том, что коэффициент логистической регрессии значительно отличается от нуля, аналогична проверке для обычной линейной регрессии.

Мы можем оценить общую эффективность логистической регрессии, изучив критерий хи-квадрат отношения правдоподобия (англ. 'chi-square test statistic').

Большинство пакетов статистического анализа рассчитывают этот критерий (статистику), а также p-значение или вероятность получения этого критерия, если нет совместного влияния независимых переменных на вероятность события.

P-значение помогает нам оценить общую статистическую значимость модели.

В логистической регрессии нет эквивалентной меры для статистики \(R^2\) в обычной линейной регрессии, поскольку логистическую регрессию нельзя подобрать ​​с использованием метода наименьших квадратов. Тем не менее, исследователи предложили для логистической регрессии различные меры, чтобы представить объясненную вариацию.

Эти меры называются псевдо-\(R^2\) и должны интерпретироваться с осторожностью. Псевдо-\(R^2\) в логистической регрессии может использоваться для сравнения различных спецификаций одной и той же модели, но не подходит для сравнения моделей, основанных на различных наборах данных.

Модели с качественными зависимыми переменными могут быть полезны не только для управления портфелем, но и для управления бизнесом. Например, мы могли бы предсказать, продолжит ли клиент инвестировать в компанию или изымет активы из компании.

Мы также могли бы объяснить, как конкретные демографические характеристики могут повлиять на вероятность того, что потенциальный инвестор станет новым клиентом, или оценить эффективность конкретной рекламной кампании, основанной на демографических характеристиках целевой аудитории.

Эти ситуации можно проанализировать с помощью логит-модели. Логистическая регрессия также играет важную роль в анализе больших данных - например, в проблемах бинарной классификации в машинном обучении и нейронных сетях.

 

Иллюстрация 26. Объяснение выбора финансирования.

Grundy и Verwijmeren (2019) исследовали, какие инвестиционные характеристики определяют выбор финансирования компании. Мы можем использовать логит-модель для решения этой задачи.

Выборка состоит из 680 инвестиций, осуществленных американскими фирмами в период с 1995 по 2017 год за счет долга и акционерного капитала, для которых известна информация о характеристиках инвестиций.

Поскольку в регрессионном анализе зависимая переменная  является бинарной переменной, используется логит-модель.

В логит-модели используются следующие переменные:

Зависимая переменная:

EQUITY = двоичная переменная, которая принимает значение 1, если для финансирования инвестиций используется акционерный капитал и 0, если используется долг.

Независимые переменные:

TANGIBLE & NON-UNIQUE = бинарная переменная, которая приобретает значение 1, если инвестиции вложены в материальный движимый актив.

R&D = бинарная переменная, которая принимает значение 1, если инвестиции имеют характеристики вложений в исследования и разработки.

LN(INVESTMENT LIFE) = натуральный логарифм ожидаемой продолжительности инвестиций в годах.

TIME UNTIL PAYOFFS = упорядоченная градационная переменная, отражающая срок до начала выплат в погашение инвестиций.

INVESTMENT LIFE UNCERTAINTY = бинарная переменная, которая принимает значение 1, если инвестиции имеют относительно неопределенный срок.

VOLATILITY = бинарная переменная, которая принимает значение 1, если инвестиции относительно более рискованны.

NEED FOR MONITORING = упорядоченная градационная переменная, основанная на оценке необходимости мониторинга инвестиций. Принимает одно из трех значений: низкая, средняя или высокая.

---

Авторы исследования изучают, связан ли выбор типа финансирования инвестиций, как за счет капитала, так и за счет долга, с характеристиками финансируемых инвестиций.

Одна гипотеза заключается в том, что акционерный капитал будет с большей вероятностью использоваться, когда инвестиции имеют большую неопределенность погашения.

Соответственно, долговое финансирование будет с большей вероятностью использоваться для инвестиций в материальные активы или инвестиций с большей потребностью в мониторинге.

Ни одна из этих гипотез не дает четкого прогноза относительно взаимосвязи между сроком инвестиций и используемым методом финансирования.

В следующей таблице показана выдержка из результатов анализа: Модель 1 Таблица II Grundy и Verwijmeren (2019).

Объяснение выбора финансирования с использованием логит-модели.

Независимые переменные	Коэффициент	Стандартная ошибка	Z-статистика
TANGIBLE & NON-UNIQUE	-1.18	0.29	-4.07
R&D	0.90	0.46	1.96
LN(INVESTMENT LIFE)	-0.39	0.26	-1.50
TIME UNTIL PAYOFFS	1.49	0.31	4.81
INVESTMENT LIFE UNCERTAINTY	0.13	0.39	0.33
VOLATILITY	1.29	0.35	3.69
NEED FOR MONITORING	-0.98	0.31	-3.16
Псевдо-\(R^2\)		0.28

Примечание: Исследование не включает z-статистику. Тем не менее, мы можем вычислить ее как отношение коэффициента к стандартной ошибке.

---

 

Как показывают результаты в таблице, абсолютное значение z-статистики для переменных TANGIBLE & NON-UNIQUE, R&D, TIME UNTIL PAYOFFS, VOLATILITY и NEED FOR MONITORING равно или больше, чем критическое значение на уровне значимости 0.05 для z-статистики (1.96).

Для каждой из этих переменных на уровне значимости 0.05 мы можем отклонить нулевую гипотезу о том, что коэффициент равен 0 в пользу альтернативной гипотезы о том, что коэффициент не равен 0.

Статистически значимые коэффициенты предполагают, что:

Таким образом, подтверждаются обе первоначальные гипотезы  в отношении факторов, которые определяют выбор фирмой типа финансирования.

Ни одна из двух оставшихся независимых переменных не является статистически значимой на уровне 0.05 в этом анализе.

Абсолютные значения z-статистик для этих двух переменных составляют 1.50 или менее, поэтому ни одно из них не достигает критического значения 1.96, необходимого для отклонения нулевой гипотезы (о том, что связанный коэффициент значительно отличается от 0).

Этот результат показывает, что после того, как мы учитываем факторы, включенные в анализ, другие факторы - срок инвестиций (LN(INVESTMENT LIFE)) и неопределенность срока инвестиций (INVESTMENT LIFE UNCERTAINTY) - не обладают силой объяснять выбор финансирования.

Коэффициентом регрессии для независимой переменной является изменение «логарифма отношения шансов» на то, что инвестиции финансируются за счет капитала, на 1 единицу изменения в этой независимой переменной, при неизменных всех прочих независимых переменных.

Рассмотрим инвестиции, не относящиеся к R&D, для которых переменная R&D принимает значение 0. Предположим, что для этих инвестиций, после того, как мы укажем значения переменной R&D и всех других независимых переменных логит-модели, мы получим -0.6577.

Таким образом, логарифм отношения шансов для этих инвестиций, которые не являются R&D и финансируются за счет капитала, равен -0.6577.

Коэффициент регрессии 0.90 для R&D подразумевает, что если эти инвестиции являются R&D, при неизменных всех прочих независимых переменных, логарифм отношения шансов для этих инвестиций, финансируемых капиталом, увеличится до -0.6577 + 0.90 = 0.2423.

Следовательно, шансы на эти R&D инвестиции, финансируемые акционерным капиталом, будут равны exp(0.2423) = 1.2742.

 

Другими словами, вероятность финансирования акционерным капиталом будет примерно в 1.27 раза выше, чем вероятность долгового финансирования:

\( \dst {p \over 1-p} = 1.2742 \),

где \(p\) - вероятность того, что инвестиции финансируются за счет капитала.

Решение этого уравнения для \(p\) дает результат 0.5603 или 56.03%. Мы также можем рассчитать это, используя Уравнение 15:

\( \dst p = {1 \over 1 \exp [-(0.2423)]} = 0.5603 \)

Экспонента коэффициента регрессии 0.90 для R&D равна:

exp(0.90) = 2.4596 (или 1.2742 / 0.5180).

Этот «логарифм отношения шансов» является коэффициентом отношения шансов на то, что инвестиции финансируются капиталом, если являются R&D, к шансам на то, что инвестиции финансируются капиталом, если они не являются R&D.