CFA - Бизнес-риск и его компоненты
Рассмотрим компоненты бизнес-риска, связанного с операционной прибылью компании - риск продаж и операционный риск, а также концепции степени операционного рычага (DOL) и маржинальной прибыли, - в рамках изучения корпоративных финансов по программе CFA.
Риск возникает как от операционной, так и от финансовой деятельности компании. Здесь мы рассматриваем, как это происходит, а также показатели, доступные аналитику для оценки риска в каждом конкретном случае.
Бизнес-риск (англ. 'business risk') представляет собой риск, связанный с операционной прибылью. Операционная прибыль подвержена риску, поскольку общая выручка также подвержена риску, как и операционные расходы.
Выручка зависит от большого числа факторов, в том числе от экономических условий, динамики отрасли (в том числе действий конкурентов), государственного регулирования и демографии.
Таким образом, цены на товары или услуги компании, или объем продаж могут отличаться от ожидаемого. Неопределенность относительно цены и количества проданных товаров и услуг мы описываем термином риск продаж (англ. 'sales risk').
Операционный риск (англ. 'operating risk') представляет собой риск, связанный со структурой операционных расходов, в частности, использования в деятельности постоянных затрат. Чем больше постоянные операционные расходы относительно переменных операционных расходов, тем выше операционный риск. Поэтому бизнес-риск представляет собой сочетание риска продаж и операционного риска.
Компании, которые работают в одном и том же направлении бизнеса в целом имеют схожие бизнес-риски.
Риск продаж.
Рассмотрим пример Impulse Robotics еще раз. Предположим, что прогнозируемый объем произведенных и проданных единиц продукции в следующем периоде составляет 100,000, но стандартное отклонение объема проданных единиц составляет 20,000.
И предположим, что цена продажи, как ожидается, составит $10, а стандартное отклонение составит $2.
Сравните эту ситуацию с компанией Tolley Aerospace, Inc., которая имеет ту же структуру затрат, но стандартное отклонение проданных единиц составляет 40,000, а стандартное отклонение цены продажи $4.
Если мы предположим, для простоты, что постоянные операционные расходы известны с достаточной определенностью, и что количество проданных единиц и цена за единицу соответствуют нормальному распределению, мы можем увидеть влияние различных рисков на операционную прибыль двух компаний посредством моделирования; полученные результаты приведены в Иллюстрации 4.
Здесь мы видим различные распределения операционной прибыли, которые являются результатом распределений количества проданных единиц и цены за единицу. Таким образом, даже если компании имеют одинаковую структуру затрат, различия в риске продаж влияют на потенциальную изменчивость прибыльности компании.
В нашем примере, Tolley Aerospace имеет более широкое распределение возможных исходов с точки зрения операционной прибыли. Такая большая изменчивость операционной прибыли означает, что Tolley Aerospace имеет больший риск продаж, чем Impulse Robotics.
Иллюстрация 4. Симуляция операционной прибыли Impulse Robotics и Tolley Aerospace.
Панель A: Impulse Robotics.
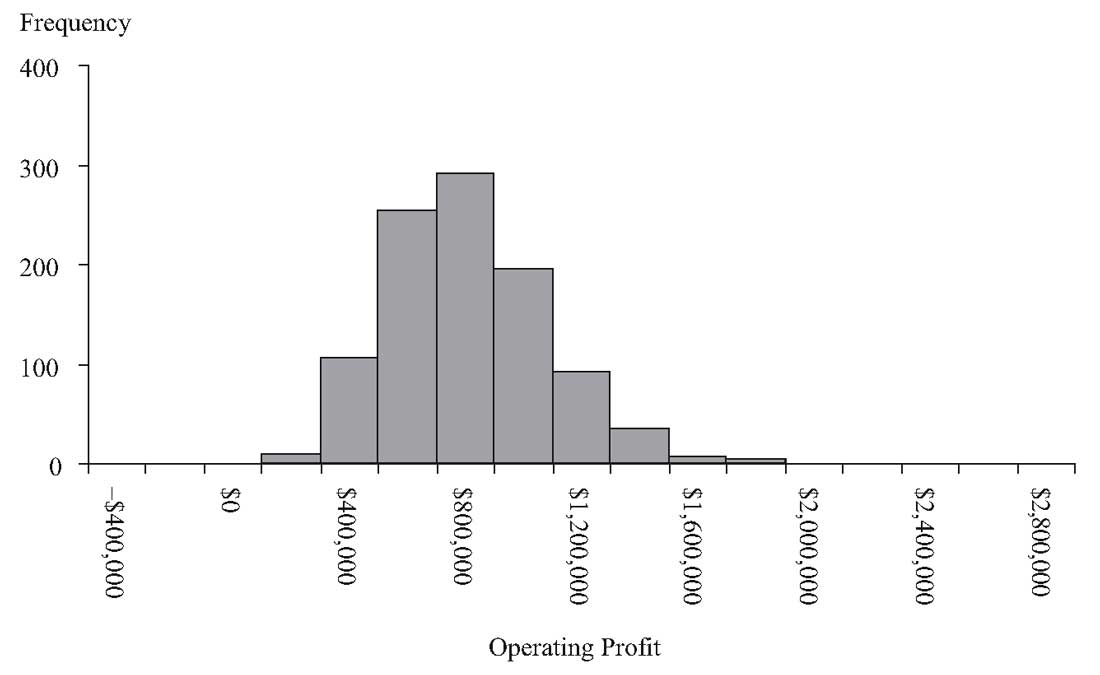
Симуляция операционной прибыли Impulse Robotics.
Панель B: Tolley Aerospace.
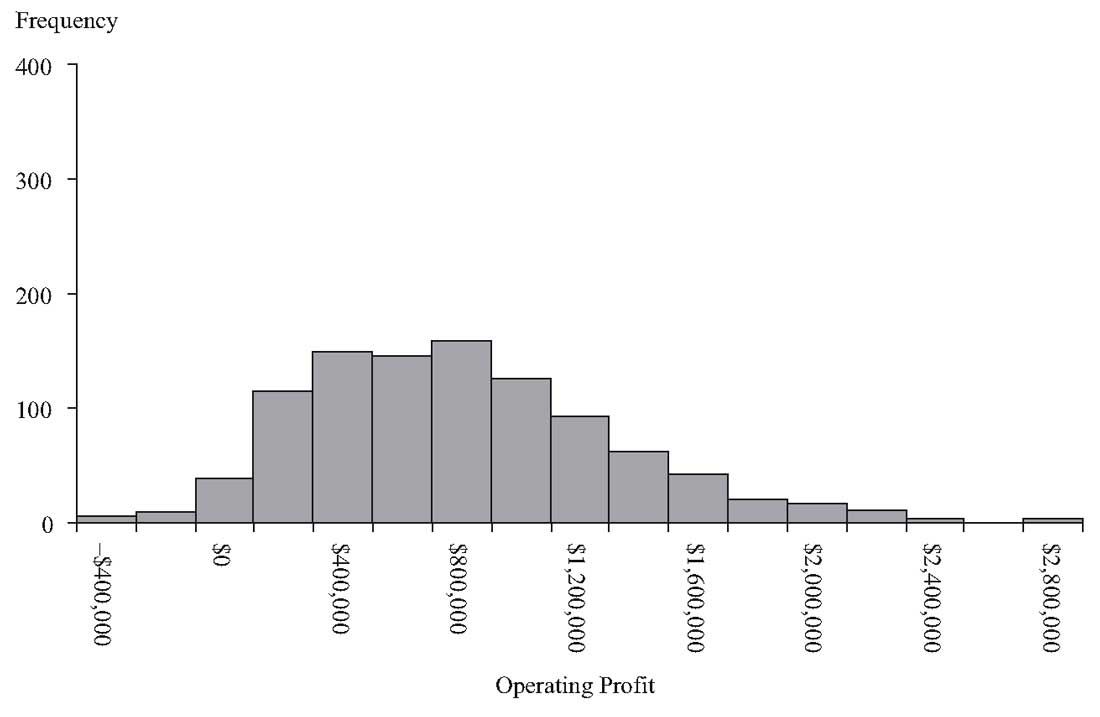
Симуляция операционной прибыли Tolley Aerospace.
Операционный риск.
Чем больше постоянная составляющая затрат, тем труднее компании скорректировать свои операционные расходы под изменения в продажах.
Соотношение постоянных и переменных расходов во многом зависит от типа бизнеса.
Даже в пределах одного направления бизнеса, компании могут менять в некоторой степени свои постоянные и переменные расходы.
Риск, возникающий из сочетания постоянных и переменных затрат мы называем термином операционный риск (англ. 'operating risk'). Чем больше постоянные операционные расходы относительно переменных операционных расходов, тем выше операционный риск.
Степень операционного рычага (эластичность операционной прибыли).
Далее мы рассмотрим, как операционный риск влияет на волатильность (изменчивость) денежных потоков.
В рамках микроэкономики вы изучали концепцию эластичности (спроса, предложения ...), которая является просто показателем чувствительности изменений одного элемента к изменениям в другом элементе.
Мы можем применить эту концепцию, чтобы понять, насколько чувствительна операционная прибыль компании к изменениям в спросе по показателю объема продаж.
Мы рассчитаем эластичность операционной прибыли, которую мы называем степенью [эффектом, уровнем, силой] операционного рычага (DOL, англ. 'degree of operating leverage').
DOL является количественным показателем операционного риска.
Степень операционного рычага представляет собой коэффициент - отношение процентного изменения операционной прибыли к процентному изменению объема продаж (количества проданных единиц).
Для упрощения предположим, что компания продает все, что она производит в тот же период. Тогда,
\(
\def\DOL{{\rm DOL}}
\)\( \dst \DOL = { \text{Процентное изменение операционной прибыли} \over \text{Процентное изменение объема продаж} } \) (Формула 1)
Например, если DOL при данном уровне объема продаж составляет 2.0, то 5-процентное увеличение объема продаж предположительно приведет к (2.0)(5%) = 10-процентному увеличению операционной прибыли.
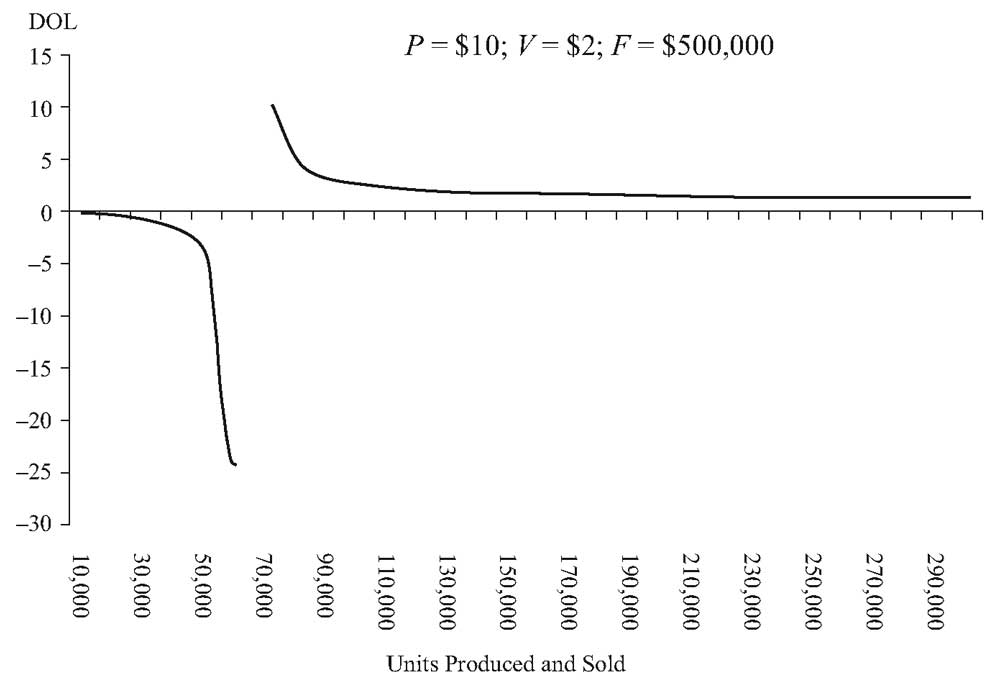
Ниже в Иллюстрации 6 показана зависимость DOL компании от уровня объема продаж.
В примере с Impulse Robotics, цена за единицу составляет $10, переменные затраты на единицу составляет $2, а общие постоянные операционные затраты составляют $500,000.
Если объем производства Impulse Robotics изменится со 100,000 единиц до 110,000 единиц, то количество проданных единиц увеличится на 10%, а операционная прибыль увеличится с $300,000 до $380,000:
Иллюстрация 5. Операционный леверидж Impulse Robotics.
|
Статья |
Продажа 100,000 ед. |
Продажа 110,000 ед. |
Процентное изменение |
|---|---|---|---|
|
Выручка |
$1,000,000 |
$1,100,000 |
+10.00 |
|
Минус переменные затраты |
200,000 |
220,000 |
+10.00 |
|
Минус постоянные затраты |
500,000 |
500,000 |
0.00 |
|
Операционная прибыль |
$300,000 |
$380,000 |
+26.67 |
Мы используем переменные и постоянные операционные расходы в наших примерах в этом чтении, чтобы проиллюстрировать концепции левериджа и точек безубыточности.
В действительности, однако, финансовый аналитик не имеет этих данных, а сталкивается с их бухгалтерской интерпретацией в отчетности, которая часто сочетает переменные и постоянные затраты, а также производственные затраты различных продуктовых линеек.
Операционная прибыль увеличивается на 26.67% при увеличении объема продаж на 10%.
Что произойдет, если объем продаж уменьшится на 10%, со 100,000 до 90,000?
Операционная прибыль составит $220,000, снизившись на 26.67%.
Мы видим, что при изменении объема продаж на 1%, операционная прибыль меняется в 2.67% в том же направлении. Если объем продаж увеличивается на 10%, операционная прибыль увеличивается на 26.7%; если объем продаж сокращается на 20%, операционная прибыль сокращается на 53.3%.
Мы можем представить степень операционного рычага, как показано в Формуле 1, разложив ее на базовые элементы:
- цену за единицу,
- переменные затраты на единицу,
- количество проданных единиц и
- постоянные операционные расходы.
Операционный прибыль - это выручка минус общие операционные расходы (переменные и постоянные компоненты затрат):
\( \dst \begin{aligned}
\stBfL {Операционная}{прибыль} &=
\text{Цена за ед. $\times$ Объем продаж} \\ &-
\text{Переменные затраты на ед. $\times$ Объем продаж} \\[1ex] &-
\text{Постоянные расходы}
\end{aligned} \)
или
\( \begin{aligned}
\stBfL {Операционная}{прибыль} &=
\underbrace { \text{Объем продаж $\bigl($Цена за ед. $-$ Переменные затраты на ед.$\bigr)$}}_{\large \text{Маржинальная прибыль}} \\ &-
\text{Постоянные расходы}
\end{aligned} \)
Маржинальная прибыль на единицу или вклад на покрытие на единицу (англ. 'per unit contribution margin') - это сумма, которую каждая проданная единица продукции вкладывает в покрытие постоянных расходов, то есть это разница между ценой за единицу и переменными затратами на единицу.
Эта разница, умноженная на объем продаж представляет собой маржинальную прибыль или вклад на покрытие (англ. 'contribution margin'), которая равна выручке за вычетом переменных затрат.
Как меняется операционная прибыль при изменении объема продаж?
Постоянные затраты не меняются. Таким образом, операционная прибыль меняется за счет маржинальной прибыли. Процентное изменение операционной прибыли для данного изменения объем продаж можно представить в виде формулы:
\( \dstl \DOL = {Q(P-V) \over Q(P-V) - F} \) (Формула 2)
где:
- \( Q \) - объем продаж,
- \( Р \) - цена за единицу,
- \( V \) - переменные операционные затраты на единицу, а
- \( F \) - постоянные операционные расходы.
Следовательно, \( P - V \) представляет собой маржинальную прибыль на единицу, а \( Q(P - V) \) является маржинальной прибылью.
Применяя формулу для DOL к данным примера Impulse Robotics, мы можем вычислить чувствительность к изменению объема продаж в 100,000 единиц:
\( \dst \DOL_{100,000} = { 100,000 ($10 - $2) \over 100,000($10 - $2) - $500,000} = 2.67 \)
DOL = 2.67 означает, что изменение объема продаж на 1% приведет к \( 1\% \times 2.67 = 2.67\% \) изменению операционной прибыли; DOL = 5 означает, что изменение объема продаж на 1% приведет к 5% изменению операционной прибыли и так далее.
Почему мы указываем в формуле, что DOL относится к определенному объему продаж (в данном случае, 100,000 единиц)? Потому что DOL отличается в зависимости от объема произведенных и проданных единиц.
Так, например, для 200,000 единиц:
\( \dst \DOL_{200,000} = { 200,000 ($10 - $2) \over 200,000($10 - $2) - $500,000} = 1.45 \)
Мы можем увидеть чувствительность DOL для различного объема произведенной и проданной продукции на графике в Иллюстрации 6.
Когда операционная прибыль отрицательна, DOL также отрицательна.
В позиции чуть ниже и чуть выше точки, где операционная прибыль равна $0, операционная прибыль наиболее чувствительна к изменениям количества произведенных и проданных единиц.
В точке, где операционная прибыль равна $0 (62,500 произведенных и проданных единиц, в этом примере), DOL не определена, так как знаменатель при расчете DOL равен $0.
После этой точки DOL постепенно снижается, поскольку все больше единиц производится и продается.
Иллюстрация 6. Степень операционного рычага Impulse Robotics для различного объема произведенных и проданных единиц продукции.
Теперь взглянем на аналогичную ситуации, в которой компания сместила часть операционных расходов с постоянных расходов в переменные расходы.
Malvey Aerospace имеет цену продажи $10, переменные затраты $6 на единицу, и $150,000 постоянных расходов.
Изменение объема продаж с 100,000 до 110,000 (на 10%) меняет операционную прибыль с $250,000 до $290,000, или на 16%. DOL в этом случае будет равен 1.6:
\( \dst \DOL_{100,000} = { 100,000(10 - $6) \over 100,000(10 - $6)- $150,000} = 1.6 \)
Изменение операционной прибыли составляет 16%:
\( \dst \begin{aligned}
\stBfL{Процентное изменение}{операционной прибыли} &=
\DOL \times \stRmL{Процентное изменение}{объема продаж} \\ &=
(1.6)(10\%) = 16\%
\end{aligned} \)
Мы можем увидеть разницу в леверидже компании Impulse Robotics and Malvey Aerospace в Иллюстрации 7.
В Панели А, мы видим, что Impulse Robotics имеет более высокую операционную прибыль, чем Malvey Aerospace, когда обе компании производят и продают более 87,500 единиц, но более низкую операционную прибыль, чем Malvey, когда обе компании производят и продают менее 87,500 единиц.
Мы можем вычислить количество единиц, которые приносят одну и ту же операционную прибыль этим двум компаниям путем приравнивания операционной прибыли и нахождения числа единиц из этого уравнения.
Пусть \( X \) - число единиц. \( X \), при котором Malvey Aerospace и Impulse Robotics получают одну и ту же операционную прибыль равно \( X \), которое решает следующее уравнение:
\( 10X - 2X - 500,000 = 10X - 6X - 150,000 \);
то есть, \( Х = 87,500 \).
Иллюстрация 7. Рентабельность и DOL для Impulse Robotics and Malvey Aerospace.
Impulse Robotics: P = $10; V = $2; F = $500,000
Malvey Aerospace: P = $10; V = $6; F = $150,000
Панель A: Операционная прибыль и количество произведенных и проданных единиц продукции.
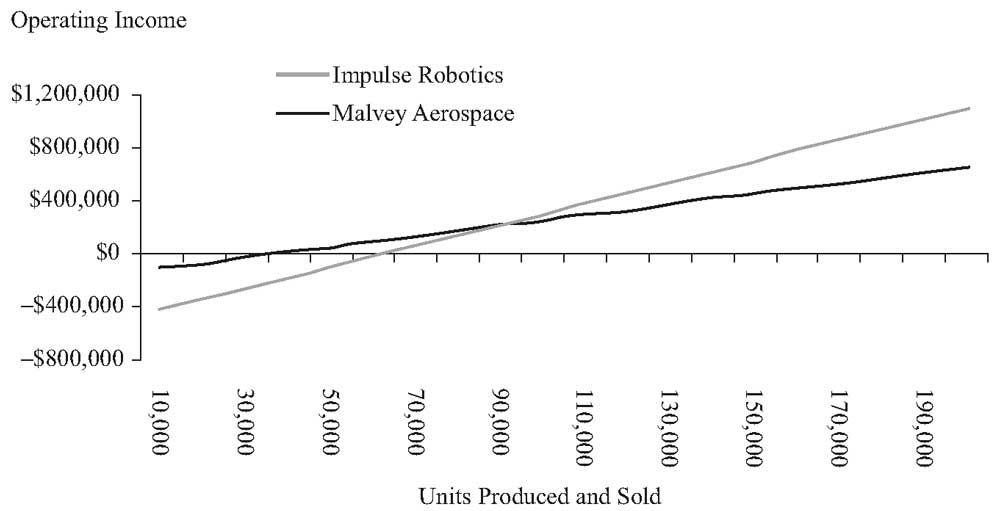
Операционная прибыль и количество произведенных и проданных единиц продукции.
Панель B: Степень операционного рычага (DOL).
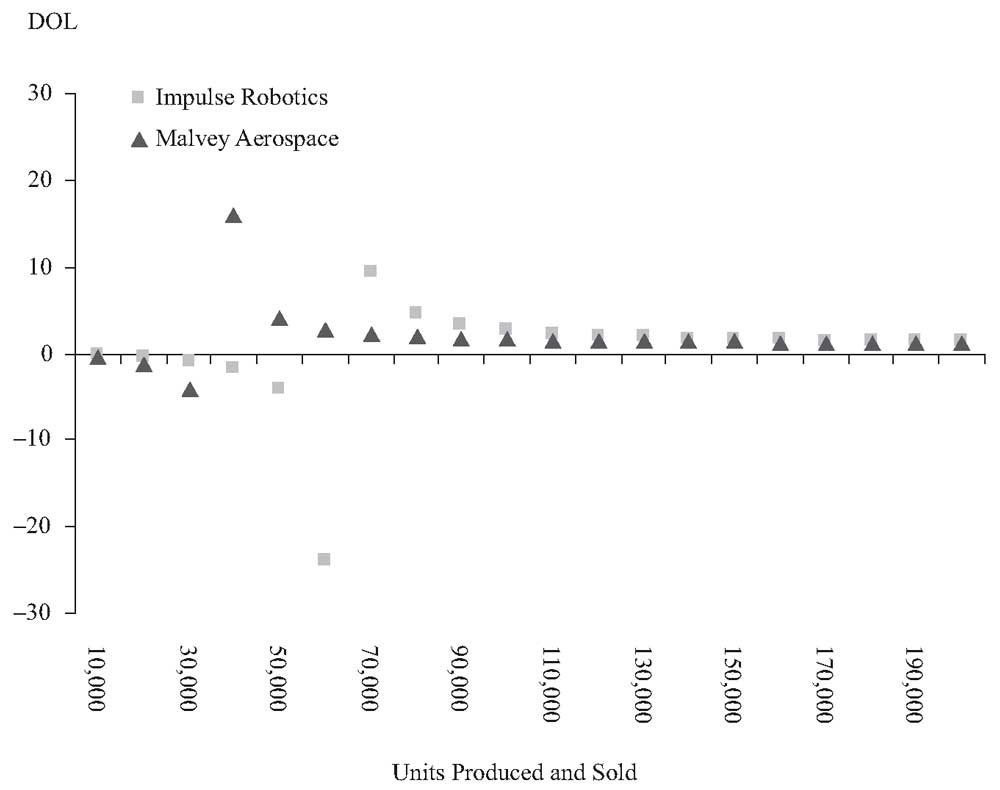
Степень операционного рычага (DOL).
Этот пример подтверждает то, что мы видели ранее в наших рассуждениях о постоянных и переменных расходах: чем больше используются постоянные расходы относительно переменных, тем более чувствительна операционная прибыль к изменениям объема продаж и, следовательно, тем выше операционный риск.
Impulse Robotics имеет больший операционный риск, поскольку у нее больший операционный рычаг. Однако, как показывает Панель B Иллюстрации 7, степени операционного рычага одинаковы для двух компаний при большом количестве произведенных и проданных единиц.
На бизнес-риски компании влияет как риск продаж, так и операционный риск. И оба этих риска определяются в значительной степени типом бизнеса компании.
Но руководство компании имеет больше возможностей для управления и контроля над операционным риском, чем над риском продаж.
Предположим, что компания решает, какое оборудование купить для производства конкретного продукта. Риск продаж при этом будет таким же, независимо от того, какое оборудование будет выбрано для производства продукта.
Но имеющееся оборудование может отличаться с точки зрения постоянных и переменных операционных затрат на производство продукта. Финансовые аналитики должны рассмотреть, как структура операционных расходов компании влияет на риск компании.
Пример (1) расчета степени операционного рычага.
Аналитик изучает потенциальное воздействие улучшения экономики на прибыль Global Auto, одного из крупнейших в мире производителей автомобилей, чья штаб-квартира находится Берлине. Global Auto производит легковые автомобили, и ее годовая выручка составляет €168 млрд.
Аналитик прогнозирует рост продаж на 10% в связи с увеличением спроса на автомобили. Он хочет видеть, как прибыль Global может отреагировать на такой уровень увеличения продаж.
Сначала он анализирует степени левериджа Global, начиная с операционного рычага.
Global продала 6 миллионов легковых автомобилей в 2017 году, со средней ценой за автомобиль €28,000; постоянными расходами, приходящимися на легковые автомобили €15 млрд. в год; и переменными затратами на автомобиль €20,500.
Какой будет степень операционного рычага Global Auto?
Решение:
\( \dst \DOL_{6 \text{ млн.}} = { 6 \text{ млн.} (\€28,000 - \€20,500) \over 6 \text{ млн.} (\€28,000 - \€20,500) - \€15 \text{ млн.}} = 1.5 \)
Операционная прибыль составляет:
[6 млн. \( \times \) (€28,000 - €20,500)] - €15 млн. = €30 млн.
При 10-процентном увеличении объема продаж автомобилей, операционная прибыль увеличивается на 1.50 \( \times \) 10% = 15.0%.
Отрасли с высокими операционными рычагами - это, как правило, те, в которых необходимы предварительные капитальные инвестиции в производство продукта, но требуется относительно мало средств на само изготовление и распространение продукта.
Этому описанию, например, соответствуют разработчики программного обеспечения и фармацевтические компании.
Кроме того, розничные торговцы имеют низкие операционные рычаги, потому что большая часть стоимости проданного товара приходится на переменные затраты.
Поскольку большинство компаний производят более одного продукта, внешнему аналитику трудно получить соотношение переменных и постоянных расходов.
Мы можем получить представление об операционном леверидже компании, глядя на взаимосвязь изменений в операционной прибыли с изменениями в продажах всей компании.
Эту взаимосвязь можно оценить с помощью регрессии изменения операционной прибыли (объясняемая переменная) с изменением в продажах (объясняющая переменная) за последний период времени.
Регрессия методом наименьших квадратов (англ. 'least-squares regression') представляет собой процедуру нахождения оптимальной кривой (так называемой кривой регрессии наименьших квадратов) с помощью набора точек данных путем минимизации квадратов отклонений от кривой.
См.: CFA - Простая линейная регрессия.
Хотя этот подход не обеспечивает точную оценку операционного риска, он может помочь получить общее представление о величине имеющихся операционных рычагов.
Например, сравните взаимосвязь между операционной прибылью и выручкой транспортной компании Delta Air Lines и розничной компании Wal-Mart Stores, как показано в Иллюстрации 8.
Следует отметить, что наклон кривой регрессии больше у Delta Air Lines (с коэффициентом наклона 0.1702), чем у Wal-Mart (с коэффициентом наклона 0.0493).
При этом не следует полагаться на визуальное сравнение наклонов, поскольку масштабы осей X и Y различны на графиках этих двух регрессий.
Мы можем видеть, что операционная прибыль более чувствительна к изменениям в выручке для более высокого операционного рычага Delta Air Lines по сравнению с более низким операционным рычагом Wal-Mart Stores.
Иллюстрация 8. Взаимосвязь между операционной прибылью и выручкой.
Панель A: Операционная прибыль и выручка Delta Airlines, 1990-2017.
Расчет регрессии:
Операционная прибыль = -$2,249 + 0.1702
Выручка \( R^2 \) = 64.73%.
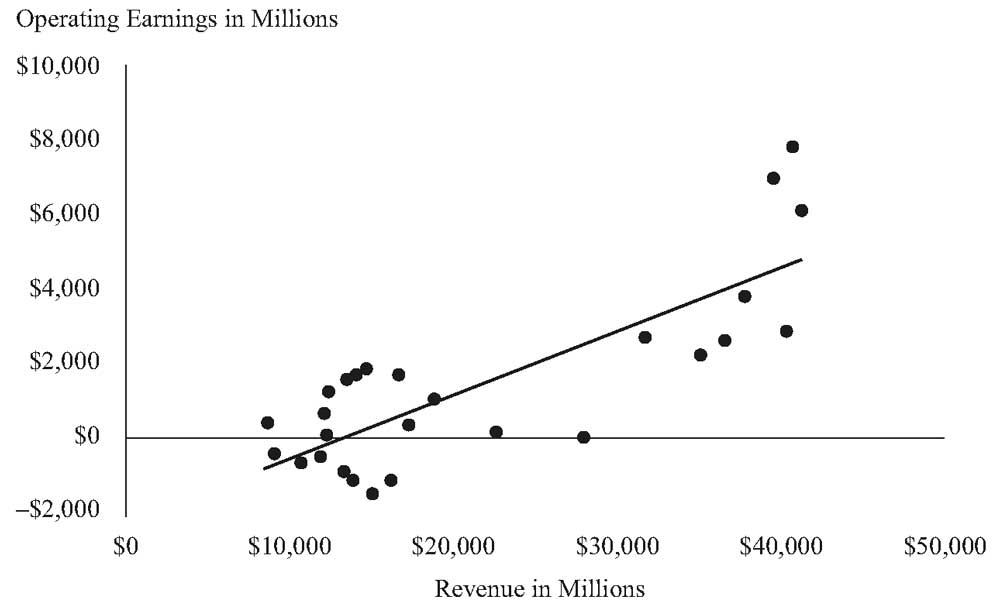
Операционная прибыль и выручка Delta Airlines, 1990-2017.
Панель B: Операционная прибыль и выручка Wal-Mart Stores, 1990-2017.
Расчет регрессии:
Операционная прибыль = $253.16 + 0.0493
Выручка \( R^2 \) = 94,89%.
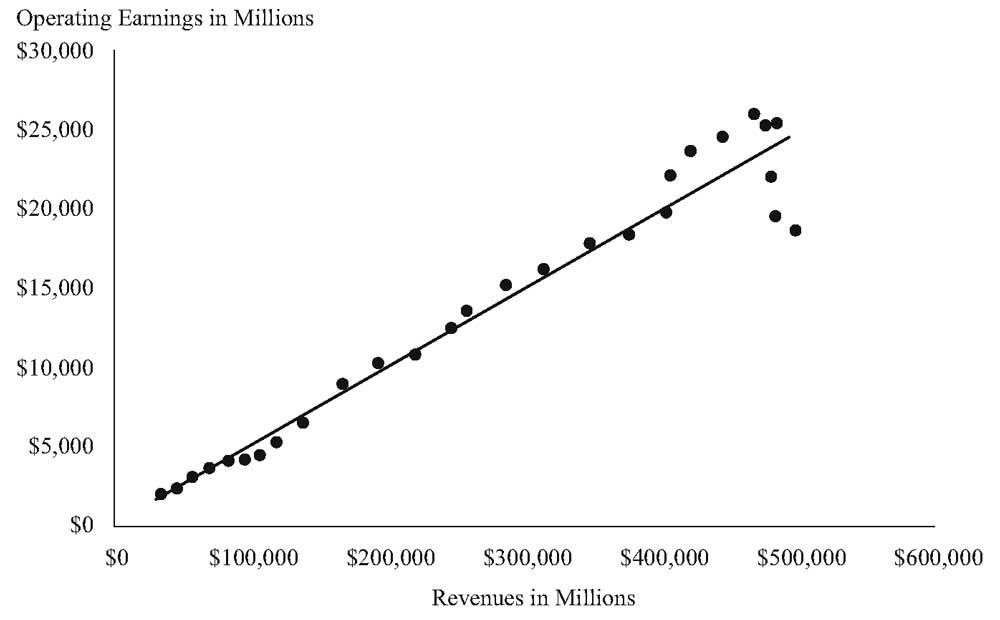
Операционная прибыль и выручка Wal-Mart Stores, 1990-2017.
Источники: Формы 10-K Delta Airlines 10-K и Wal-Mart Stores.