CFA - Простая линейная регрессия
Рассмотрим простую линейную регрессию на примере анализа факторов, управляющих рентабельностью активов (ROA), - в рамках изучения количественных методов по программе CFA (Уровень II).
Финансовым аналитикам часто требуется выяснить, полезна ли переменная для объяснения другой переменной.
Например, аналитик может захотеть узнать, помогает ли рост прибыли или, возможно, рост денежных потоков объяснить стоимость компании на рынке. Регрессионный анализ (англ. 'regression analysis') - это инструмент для решения вопросов этого типа.
Предположим, что аналитик изучает рентабельность активов (ROA) в отрасли и наблюдает за ROA шести компаний, показанных в Иллюстрации 1.
Среднее значение этих ROA составляет 12.5%, но диапазон значений составляет от 4% до 20%.
Иллюстрация 1. Рентабельность активов отдельных компаний.
|
Компания |
ROA (%) |
|
A |
6 |
|
B |
4 |
|
C |
15 |
|
D |
20 |
|
E |
10 |
|
F |
20 |
Пытаясь понять, почему ROA этих компаний отличаются друг от друга, мы могли бы разобраться,
- почему ROA компании A отличается от ROA компании B,
- почему ROA компании A отличается от ROA компании D,
- почему ROA компании F отличается от ROA компании C,
- и т.д., сравнивая каждую пару ROA.
Более простой способ провести это исследование - попытаться понять, почему ROA каждой компании отличается от среднего ROA в 12.5%.
Для этого мы смотрим на сумму квадратных отклонений наблюдений от среднего значения, чтобы понять вариации ROA по отношению к их среднему значению.
Пусть \(Y\) представляет переменную, которую мы хотели бы объяснить, которая в данном случае является рентабельностью активов.
Пусть \(Y\) представляет наблюдаемое ROA компании, и пусть \(\overline{Y}\) представляет среднее ROA для выборки размера \(n\).
Мы можем описать вариацию ROA как:
\( \dstl
\text{Вариация } \ Y = \sum^{n}_{i=1} (Y_i - \overline Y) ^2
\) (1)
Наша цель состоит в том, чтобы понять, что движет этой рентабельностью активов или, другими словами, что объясняет вариацию \(Y\).
Вариацию \(Y\) часто называют общей суммой квадратов (SST, sum of squares total) или суммой квадратов отклонений.
Теперь мы спрашиваем, можно ли объяснить вариацию ROA, используя другую переменную, которая также варьируется среди компаний.
Обратите внимание, что если эта другая переменная является постоянной или случайной величиной, она не поможет объяснить, почему ROA отличаются друг от друга.
Предположим, что аналитик считает, что капитальные затраты за предыдущий период, связанные с закупкой основных средств, являются движущей силой переменной ROA.
Давайте представляем эту переменную капитальных затрат как CAPEX в Иллюстрации 2.
Иллюстрация 2. Рентабельность активов и капитальные затраты.
|
Компания |
ROA (%) |
CAPEX (%) |
|
A |
6.0 |
0.7 |
|
B |
4.0 |
0.4 |
|
C |
15.0 |
5.0 |
|
D |
20.0 |
10.0 |
|
E |
10.0 |
8.0 |
|
F |
20.0 |
12.5 |
|
Среднее арифметическое |
12.50 |
6.10 |
Вариация \(X\), в данном случае CAPEX, рассчитывается как:
\( \dstl
\text{Вариация } \ X = \sum^{n}_{i=1} (X_i - \overline X) ^2
\) (2)
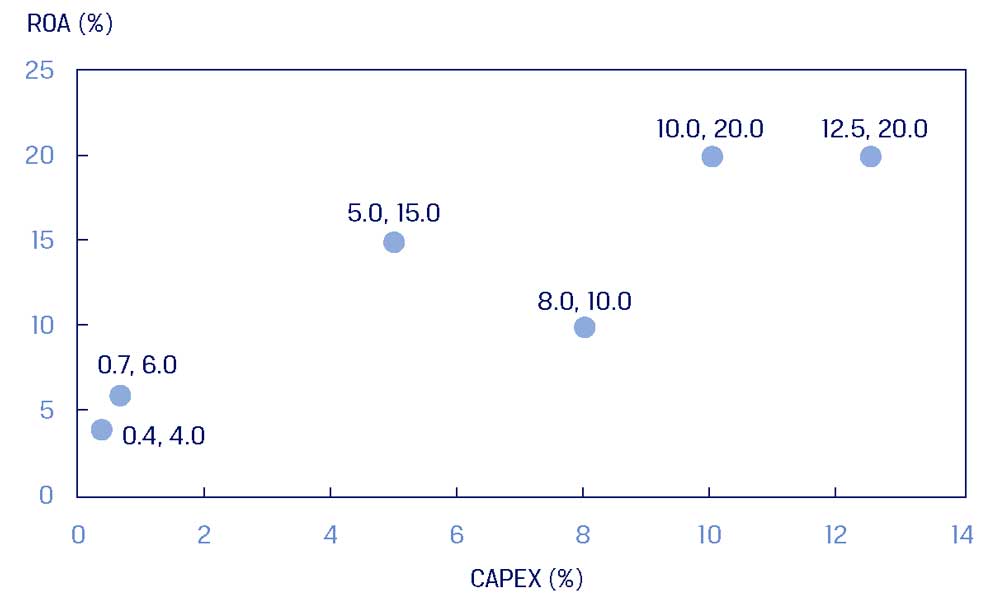
Мы можем увидеть связь между ROA и CAPEX на диаграмме рассеяния (рассеивания) или точечном графике (англ. 'scatter plot') в Иллюстрации 3, который показывает две переменные в двух измерениях.
Как правило, мы представляем переменную, чье изменение (вариацию) мы хотим объяснить по вертикальной оси, а переменную, чье изменение мы хотим использовать для объяснения этого изменения (вариации) - на горизонтальной оси.
Каждая точка на этом точечном графике представляет собой парное наблюдение, которое состоит из CAPEX и ROA.
Простой визуальный осмотр позволяет сделать вывод, что по-видимому, существует положительная связь между ROA и CAPEX: компании с более высоким CAPEX, как правило, имеют более высокий ROA.
Иллюстрация 3. График рассеяния ROA и CAPEX.
В примере с ROA мы используем капитальные затраты, чтобы объяснить рентабельность активов.
Мы называем переменную, вариация которой объясняется, зависимой переменной (англ. 'dependent variable') или объясняемой переменной (англ. 'explained variable'); она обычно обозначается как \(Y\).
Мы называем переменную, вариация которой используется для объяснения вариации зависимой переменной - независимой переменной (англ. 'independent variable') или объясняющей переменной (англ. 'explanatory variable'); она обычно обозначается как \(X\).
Следовательно, в нашем примере ROA является зависимой переменной \(Y\), а CAPEX является независимой переменной \(X\).
Общим методом нахождения зависимых и независимых переменных является оценка линейной связи, которая подразумевает описание взаимосвязи между двумя переменными, представленной прямой линией.
Если у нас есть только одна независимая переменная, мы называем этот метод простой линейной регрессией (SLR, simple linear regression).
Если у нас есть больше одной независимой переменной, мы называем этот метод множественной регрессией (multiple regression).
Линейная регрессия позволяет нам проверять гипотезы о взаимосвязи между двумя переменными, путем количественной оценки силы взаимосвязи между двумя переменными, и использовать одну переменную для прогнозирования другой переменной.
Здесь мы уделяем внимание линейной регрессии с одной независимой переменной, то есть простой линейной регрессии.
Пример 1. Выявление зависимых и независимых переменных в регрессии.
Аналитик изучает взаимосвязь между ростом прибыли и доходностью акций корпорации. В частности, она интересуется, влияет ли пересмотр прибыли на доходность акций за тот же период.
Она собирает ежемесячные данные за 5 лет об EPS (прибыли на акцию) для выборки из 100 компаний, а также их ежемесячную доходность цены на акции в течение пятилетнего периода.
Каковы зависимые и независимые переменные в ее модели?
Решение.
Зависимой переменной является ежемесячная доходность цен на акции, а независимая переменная - это EPS, поскольку в модели аналитика вариация ежемесячной доходности цен на акции объясняется вариацией EPS.