CFA - Проблема нескольких IRR и проблема отсутствия IRR
Нестандартные модели денежных потоков инвестиционного проекта могут привести к множественным значения IRR и отсутствию IRR. Рассмотрим эти проблемы и их решение на примерах, - в рамках изучения корпоративных финансов по программе CFA.
Одна из проблем с использованием критерия IRR - это «проблема множественной IRR» (англ 'multiple IRR problem').
Мы можем проиллюстрировать эту проблему на следующей нетрадиционной модели движения денежных потоков:
|
Время |
0 |
1 |
2 |
|
Денежный поток |
-1,000 |
5,000 |
-6,000 |
*Этот пример адаптирован из Hirschleifer.
IRR для этих денежных потоков удовлетворяет следующему уравнению:
\( \dst -1,000 + {5,000 \over (1+\IRR)^1}+ {-6,000 \over (1+\IRR)^2} = 0 \)
Оказывается, что есть два значения IRR, которые удовлетворяют уравнению:
IRR = 1 = 100% и IRR = 2 = 200%.
Чтобы еще лучше понять эту проблему, рассмотрите профиль NPV для этой инвестиции, который показан в иллюстрациях 14 и 15.
Как вы можете видеть в профиле NPV, NPV равна нулю при IRR = 100% и IRR = 200%. NPV отрицательна для ставок дисконтирования ниже 100%, затем положительна для ставок от 100% до 200%, а затем опять отрицательна для ставок выше 200%. NPV достигает наивысшего значения, когда ставка дисконтирования составляет 140%.
Также бывают инвестиционные проекты без IRR.
«Проблема отсутствия IRR» (англ. 'no-IRR problem') возникает при такой модели денежных потоков:
|
Время |
0 |
1 |
2 |
|
Денежный поток |
100 |
-300 |
250 |
IRR для этих денежных потоков удовлетворяет следующему уравнению:
\( \dst 100 + {-300 \over (1+\IRR)^1}+ {250 \over (1+\IRR)^2} = 0 \)
Для этих денежных потоков не существует ставки дисконтирования, которая приводит к нулевой NPV.
Означает ли это, что проект не подходит для инвестиции?
В данном случае проект на самом деле является выгодным для инвестиций. Как показывают иллюстрации 16 и 17, NPV является положительным для всех ставок дисконтирования.
Самый низкий NPV, со значением 10, соответствует ставке дисконтирования 66.67%, и NPV всегда выше нуля. Следовательно, IRR не существует.
Иллюстрация 14. Профиль NPV при множественной IRR.
|
Ставка дисконтирования (%) |
NPV |
|---|---|
|
0 |
-2,000.00 |
|
25 |
-840.00 |
|
50 |
-333.33 |
|
75 |
-102.04 |
|
100 |
0.00 |
|
125 |
37.04 |
|
140 |
41.67 |
|
150 |
40.00 |
|
175 |
24.79 |
|
200 |
0.00 |
|
225 |
-29.59 |
|
250 |
-61.22 |
|
300 |
-125.00 |
|
350 |
-185.19 |
|
400 |
-240.00 |
|
500 |
-333.33 |
|
1,000 |
-595.04 |
|
2,000 |
-775.51 |
|
3,000 |
-844.95 |
|
4,000 |
-881.62 |
|
10,000 |
-951.08 |
|
1,000,000 |
-999.50 |
Иллюстрация 15. График профиля NPV при множественной IRR.
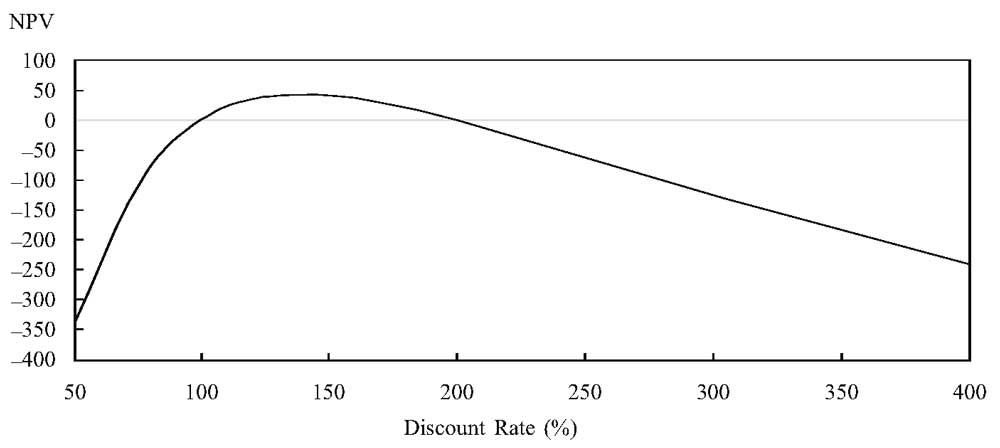
График профиля NPV при множественной IRR.
Иллюстрация 16. Профиль NPV для инвестиционного проекта без IRR.
|
Ставка дисконтирования (%) |
NPV |
|---|---|
|
0 |
50.00 |
|
25 |
20.00 |
|
50 |
11.11 |
|
66.67 |
10.00 |
|
75 |
10.20 |
|
100 |
12.50 |
|
125 |
16.05 |
|
150 |
20.00 |
|
175 |
23.97 |
|
200 |
27.78 |
|
225 |
31.36 |
|
250 |
34.69 |
|
275 |
37.78 |
|
300 |
40.63 |
|
325 |
43.25 |
|
350 |
45.68 |
|
375 |
47.92 |
|
400 |
50.00 |
Иллюстрация 17. График профиля NPV для инвестиционного проекта без IRR.
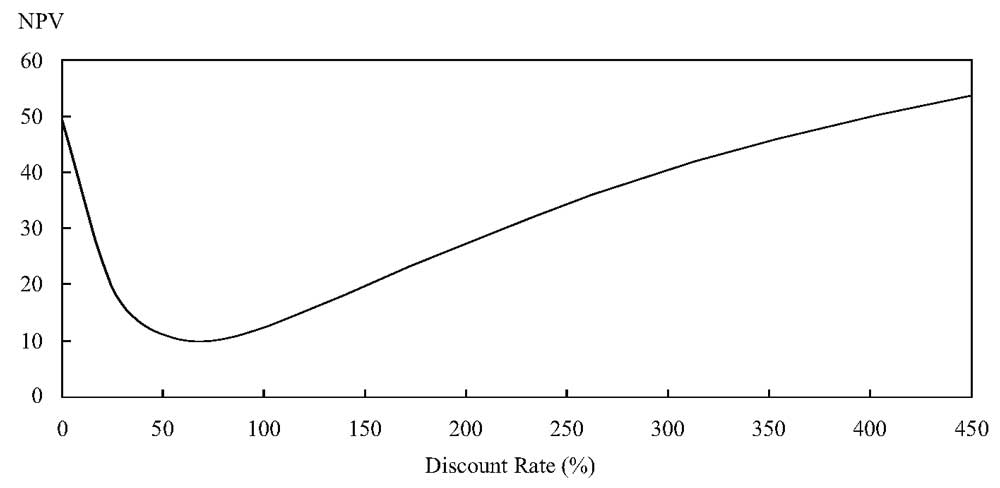
График профиля NPV для инвестиционного проекта без IRR.
Для обычных проектов, в которых за первоначальными затратами следуют денежные поступления (отрицательные потоки денежных средств с последующим положительным потоками денежных средств) - проблемы с несколькими IRR нет.
Однако для нетрадиционных проектов, как в примере выше, может возникнуть проблема множественной IRR.
См. также: об отличиях моделей денежных потоков.
Уравнение IRR по существу является полиномом n-й степени. Математически, полином n-й степени может иметь до n решений, хотя количество его реальных решений не может превышать количество изменений знака денежных потоков.
Например, проект с двумя изменениями знака может иметь 0, 1 или 2 IRR. Наличие двух изменений знака не означает, что у вас будет несколько IRR; это просто означает, что такое возможно.
К счастью, при бюджетировании капитала большинство проектов имеют только одну IRR. Финансовые аналитики должны знать о необычных моделях денежных потоков, которые могут привести к проблеме с несколькими значениями IRR.
