CFA - Взаимосвязь между ценой и характеристиками облигации
Рассмотрим зависимости между ценой облигации и ее основными характеристиками: рыночной ставкой дисконтирования, сроком погашения, купоном и прочими факторами ценообразования, - в рамках изучения ценных бумаг с фиксированным доходом по программе CFA.
Цена облигации с фиксированной ставкой будет меняться при изменении рыночной ставки дисконтирования.
Есть четыре зависимости между изменением цены облигаций и рыночной ставкой дисконтирования:
- Цена облигаций обратно зависима от рыночной ставки дисконтирования. Когда рыночная ставка дисконтирования увеличивается, цена облигации уменьшается (обратный эффект).
- Для той же купонной ставки и оставшегося срока погашения процентное изменение цены будет выше (в абсолютном значении, т.е. без учета знака изменения), когда рыночная ставка дисконтирования уменьшается, чем когда она увеличивается (эффект выпуклости).
- Для того же оставшегося срока погашения у облигации с меньшим купоном будет большее процентное изменение цены, чем у облигации с большим купоном, когда их рыночные ставки дисконтирования изменяются на одинаковое значение (эффект купона).
- Как правило, для той же купонной ставки у облигации с более длинным сроком погашения будет большее процентное изменение цены, чем у облигации с более коротким сроком погашения, когда их рыночные ставки дисконтирования изменяются на одинаковое значение (эффект срока погашения).
Иллюстрация 1 показывает эти зависимости на примере девяти облигаций с годовыми купонными выплатами. Облигации имеют разные купонные ставки и оставшиеся сроки погашения, но в остальном они одинаковы с точки зрения риска.
Ставки купона составляют 10%, 20%и 30% для облигаций со сроком погашения 10, 20 и 30 лет, соответственно.
Сначала все облигации оцениваются по рыночной ставке дисконтирования 20%. Для оценки используется Формула 1.
Затем рыночная ставка дисконтирования снижается на 1 процентный пункт, с 20% до 19%, а затем увеличивается с 20% до 21%.
Иллюстрация 1. Взаимосвязь между ценами и характеристиками облигаций.
|
Ставки |
Ставки |
||||||
|---|---|---|---|---|---|---|---|
|
Облигация |
Купонная ставка |
Срок погашения |
Цена при |
Цена при |
% изменение |
Цена при |
% изменение |
|
A |
10.00% |
10 |
58.075 |
60.950 |
4.95% |
55.405 |
-4.60% |
|
B |
20.00% |
10 |
100.000 |
104.339 |
4.34% |
95.946 |
-4.05% |
|
C |
30.00% |
10 |
141.925 |
147.728 |
4.09% |
136.487 |
-3.83% |
|
D |
10.00% |
20 |
51.304 |
54.092 |
5.43% |
48.776 |
-4.93% |
|
E |
20.00% |
20 |
100.000 |
105.101 |
5.10% |
95.343 |
-4.66% |
|
F |
30.00% |
20 |
148.696 |
156.109 |
4.99% |
141.910 |
-4.56% |
|
G |
10.00% |
30 |
50.211 |
52.888 |
5.33% |
47.791 |
-4.82% |
|
H |
20.00% |
30 |
100.000 |
105.235 |
5.23% |
95.254 |
-4.75% |
|
I |
30.00% |
30 |
149.789 |
157.581 |
5.20% |
142.716 |
-4.72% |
Первая зависимость заключается в том, что цена облигаций и рыночная ставка дисконтирования имеют обратную зависимость. Все цены облигаций в Иллюстрации 1 растут, когда ставки снижаются с 20% до 19%, и все цены снижаются, когда ставки повышаются с 20% до 21%.
Это происходит из-за фиксированных денежных потоков у облигации с фиксированной ставкой. Числитель в Формуле 1 не меняется, когда рыночная ставка дисконтирования в знаменателе растет или падает. Следовательно, цена (PV) меняется обратно пропорционально рыночной ставке дисконтирования (\(r\)).
Вторая зависимость отражает эффект выпуклости. В Иллюстрации 1 процентные изменения цены рассчитываются с использованием этой формулы:
\( \textbf{% Изменение} = \dst {\textbf{Новая цена} \ - \ \textbf{Старая цена} \over \textbf{Старая цена} } \)
Например, когда ставка дисконтирования рынка падает для Облигации A, ее цена увеличивается с 58.075 до 60.950. Процентное увеличение цены составляет 4.95%.
\( \textbf{% Изменение} = \dst { 60.950 - 58.075 \over 58.075 } = 0.0495 \)
Для каждой облигации процентное увеличение цены в абсолютном значении больше, чем снижение цены в процентном выражении.
Это подразумевает, что взаимосвязь между ценой облигации и рыночной ставкой дисконтирования не является линейной; вместо этого она представляет кривую. Эту кривую можно описать как «выпуклую вниз». Эффект выпуклости показан в Иллюстрации 2 для 10% 10-летней облигации.
Иллюстрация 2. Выпуклая вниз кривая зависимости между рыночной ставкой дисконтирования и ценой 10-летней 10% облигации.
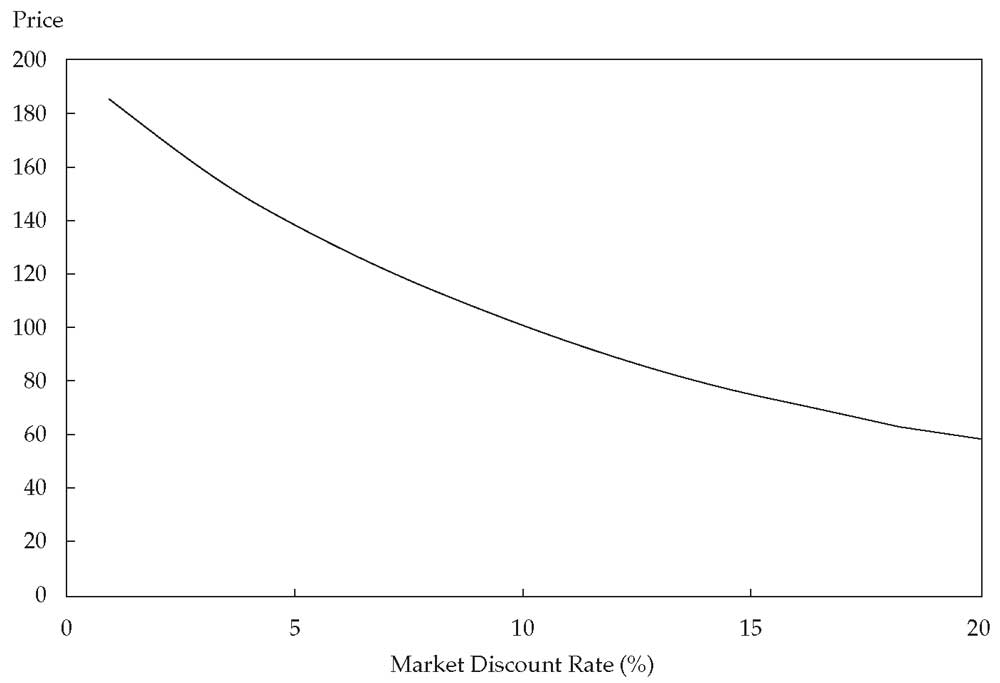
Выпуклая вниз кривая зависимости между рыночной ставкой дисконтирования и ценой 10-летней 10% облигации.Третья зависимость - это эффект купона. Рассмотрим Облигации A, B и C со сроком погашения 10 лет. Как при уменьшении, так и при увеличении доходности к погашению Облигация A имеет большее процентное изменение цены, чем Облигация B, а Облигация B имеет большее изменение, чем Облигация C.
Тот же принцип действует также для 20-летних и 30-летних облигаций. Следовательно, облигации с более низким купоном имеют большую ценовую волатильность, чем облигации с более высоким купоном, при прочих равных.
Четвертая зависимость - это эффект срока погашения. Сравните результаты для Облигаций A и D, для Облигаций B и E, а также для Облигаций C и F. 20-летние облигации имеют большее процентное изменение цены, чем 10-летние облигации, как при увеличении, так и при уменьшении рыночной ставки дисконтирования.
В целом, долгосрочные облигации имеют большую ценовую волатильность, чем краткосрочные облигации, при прочих равных.
Из эффекта срока погашения есть исключения. Вот почему слово «в целом» присутствует в вышеприведенном утверждении. Сравните результаты в Иллюстрации 1 для Облигаций D и G, для Облигаций E и H, а также для Облигаций F и I.
Облигаций с большим купоном F и I продаются с премией. Эти 30-летние облигации имеют большее процентное изменение цен, чем 20-летние облигации. Тот же принцип действует для облигаций E и H, которые первоначально оценивались по номинальной стоимости.
Исключение показано в результатах для облигаций D и G, которые оцениваются с дисконтом, поскольку их ставка купона ниже, чем рыночная ставка дисконтирования. 20-летняя 10% облигация имеет более высокое процентное изменение цены, чем 30-летняя 10% облигации.
Исключения из эффекта срока погашения редки на практике. Они встречаются только для долгосрочных облигаций с низким купоном (но не бескупонных облигаций), которые продаются с дисконтом.
Эффект срока погашения всегда присутствует для бескупонных облигаций, как и для облигаций, оцененных по номинальной стоимости или с премией к номинальной стоимости.
Последний момент, который следует отметить в Иллюстрации 1, заключается в том, что Облигации B, E и H с купонной ставкой 20% продаются по номинальной стоимости, когда рыночная ставка дисконтирования составляет 20%. Облигация, имеющая ставку купона, равную рыночной ставке дисконтирования, оценивается по номинальной стоимости на дату выплаты купона, независимо от количества лет до погашения.
Пример 3. Процентное изменение цен облигаций в зависимости от купона и оставшегося срока погашения.
Инвестор рассматривает следующие шесть государственных облигаций с годовым купоном:
|
Облигация |
Купонная ставка |
Оставшийся |
Доходность |
|---|---|---|---|
|
A |
0% |
2 года |
5.00% |
|
B |
5% |
2 года |
5.00% |
|
C |
8% |
2 года |
5.00% |
|
D |
0% |
4 года |
5.00% |
|
E |
5% |
4 года |
5.00% |
|
F |
8% |
4 года |
5.00% |
- Исходя из зависимости между ценами и характеристиками облигаций, какая облигация увеличится в цене больше всех на процентной основе, если доходность всех облигаций снизится с 5.00% до 4.90%?
- Исходя из зависимости между ценами и характеристиками облигаций, какая облигация уменьшится в цене меньше всех на процентной основе, если доходность всех облигаций увеличится с 5.00% до 5.10%?
Решение для части 1:
Облигация D будет расти в цене на процентной основе больше всех, потому что она имеет самую низкую купонную ставку (эффект купона) и более длительный срок погашения (эффект срока погашения).
В этих облигациях нет исключения из эффекта срока погашения, потому среди них нет облигаций с низким купоном, продающихся с дисконтом.
Решение для части 2:
Облигация C снизится в цене на процентной основе меньше всех, потому что она имеет самую высокую купонную ставку (эффект купона) и более короткий сроку погашения (эффект срока погашения).
Из эффекта срока погашения нет исключений, потому что Облигации C и F оцениваются с премией к номиналу.
Иллюстрация 2 демонстрирует влияние на цену облигаций, исходя из предположения, что оставшийся срок до погашения не меняется.
Цены на облигации меняются с течением времени, даже если рыночная ставка дисконтирования остается прежней. Со временем держатель облигации приближается к моменту получения номинальной стоимости при погашении.
Траектория цены при постоянной доходности иллюстрирует изменение цены на облигацию с фиксированным доходом с течением времени. Эта траектория показывает влияние эффекта «стремления номиналу» на цену облигации, продающейся с премией или дисконтом к номинальной стоимости.
Если эмитент не подвергается дефолту, цена облигации стремится к номинальной стоимости по мере того, как ее оставшийся срок погашения стремится к нулю.
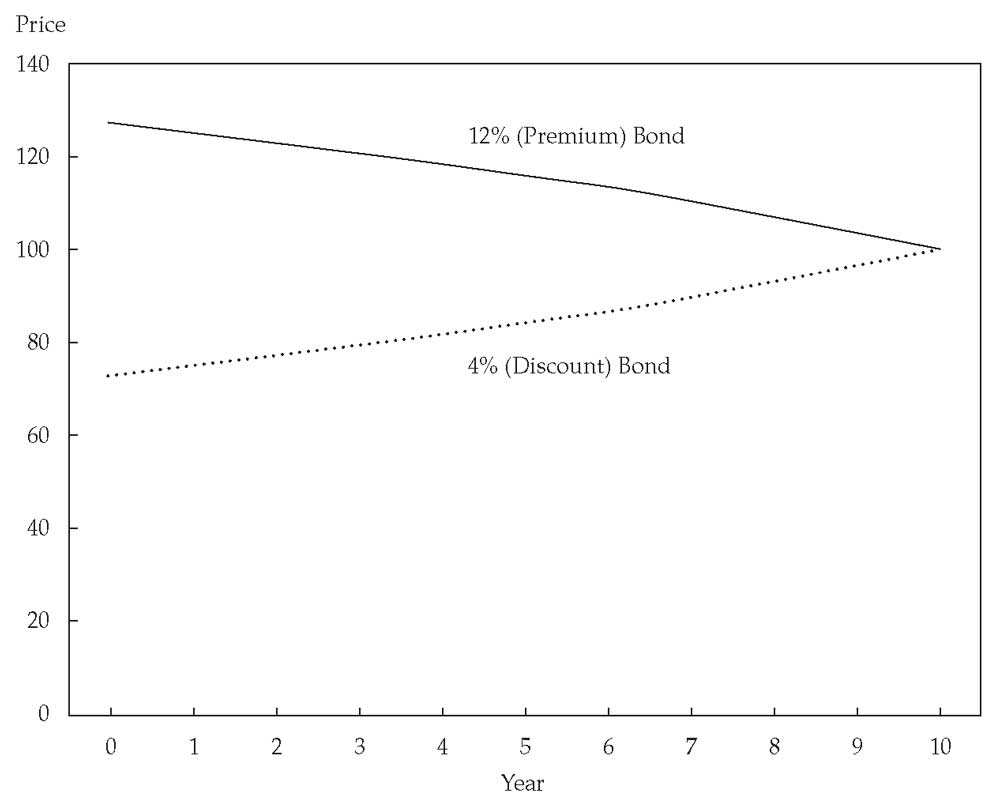
Иллюстрация 3 показывают траектории цен для 10-летних облигаций с 4% и 12% годовыми купонными выплатами. Обе облигации имеют рыночную ставку дисконтирования 8%. Первоначальная цена 4% облигации составляет 73.160 на 100 номинальной стоимости.
Цена увеличивается каждый год и стремится к номинальной стоимости по мере приближения даты погашения. Первоначальная цена 12% облигации составляет 126.840, и она уменьшается с каждым годом, приближаясь к номинальной стоимости по мере приближения срока погашения. Обе цены «стремятся к номиналу».
Иллюстрация 3. Траектории цен 10-летних облигаций с 4% и 12% годовыми купонными выплатами при рыночной ставке дисконтирования 8%.
|
Дисконтная облигация |
73.160 |
75.012 |
77.013 |
79.175 |
81.508 |
84.029 |
86.751 |
89.692 |
92.867 |
96.296 |
100.00 |
|
Премиумная облигация |
126.84 |
124.98 |
122.98 |
120.82 |
118.49 |
115.97 |
113.24 |
110.30 |
107.13 |
103.70 |
100.00 |