Есть множество причин, по которым может отличаться доходность к погашению любых двух облигаций.

Предположим, что доходность к погашению выше по Облигации X, чем по Облигации Y. Ниже приведены некоторые возможные причины разницы между доходностью:

  • Валюта - Облигация X может быть номинирована в валюте с более высоким ожидаемым темпом инфляции, чем валюта, в которой номинирована Облигация Y.
  • Кредитный риск - Облигация X может иметь кредитный рейтинг BB неинвестиционного уровня, а Облигация Y может иметь рейтинг инвестиционного уровня AA.
  • Ликвидность - Облигация X может быть неликвидной, а Облигация Y может активно обращаться.
  • Налоговый статус - Процентный доход по Облигации X может облагаться налогом, тогда как процентный доход по Облигации Y может быть освобожден от налогообложения.
  • Периодичность - Облигация X может выплачивать один годовой купон, а ее доходность к погашению может котироваться с периодичностью 1. Облигация Y может выплачивать купон ежемесячно, а ее доходность к погашению может быть аннуализирована с периодичностью 12.

Очевидно, что еще одна причина заключается в том, что Облигация X и Облигация Y могут иметь разные оставшиеся сроки погашения. Этот фактор, объясняющий различия в доходности, называется структурой сроков погашения процентных ставок (англ. 'maturity structure', 'term structure').

Структура сроков погашения включает анализ кривых доходности, которые отражают взаимосвязь между доходностью к погашению и оставшимся сроком погашения. Существуют различные типы кривых доходности, в зависимости от характеристик облигаций.

Теоретически, структуру сроков погашения следует анализировать для облигаций, обладающих одинаковыми характеристиками, кроме оставшихся сроков погашения.

Облигации должны быть номинированы в одинаковой валюте и иметь одинаковый кредитный риск, ликвидность и налоговый статус. Их годовые ставки должны котироваться с одинаковой периодичностью. Кроме того, они должны иметь одинаковую ставку купона, чтобы каждая из них имела одинаковый уровень риска реинвестирования купонов.

На практике структура сроков погашения анализируется для облигаций, для которых эти строгие допущения плохо соблюдаются.

Идеальным набором данных для анализа будет доходность к погашению по серии государственных бескупонных облигаций с полным диапазоном сроков погашения. Эти данные представляют собой кривую спотовых ставок доходности или спотовую кривую (англ. 'spot curve') государственной облигации, которую иногда называют нулевой или «раздельной» (strip) кривой, потому что купонные платежи «отделены» от облигаций.

Спотовая кривая представляет собой последовательность ставок доходности к погашению по бескупонным облигациям. Часто эти государственные спотовые ставки интерпретируются как «безрисковая» доходность; в этом контексте «безрисковый» относится только к риску дефолта. Для инвестора все еще может быть значительный риск инфляции, а также риск ликвидности.

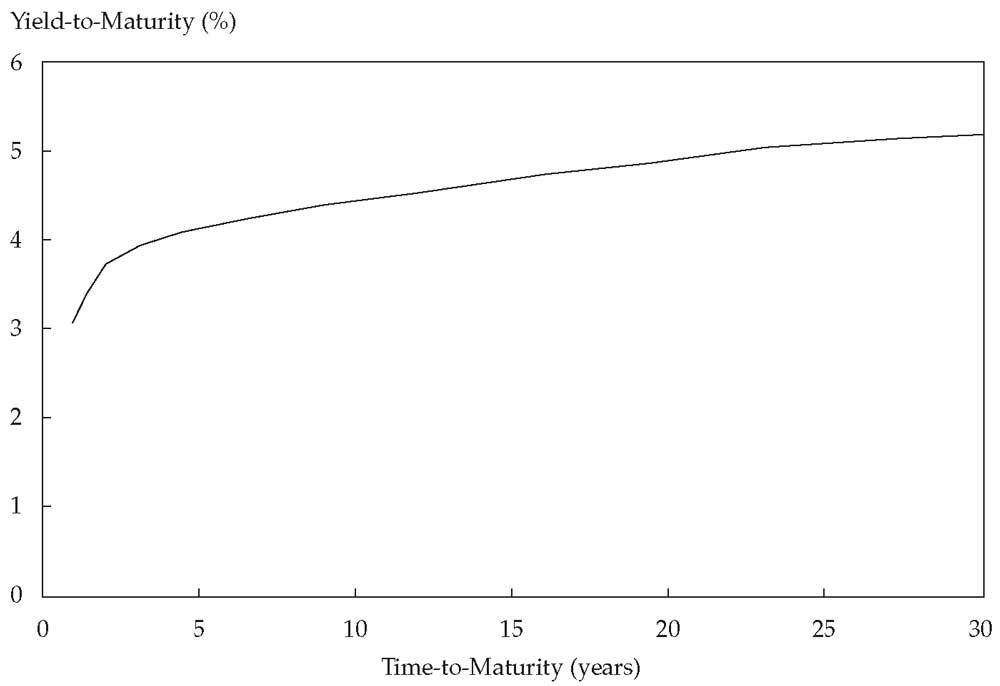
Спотовая кривая государственной облигаций показана в Иллюстрации 5 для сроков погашения от 1 до 30 лет. Годовая доходность указывается на полугодовой основе, что облегчает сравнение с купонными облигациями, которые производят полугодовые выплаты.

Иллюстрация 5. Спотовая кривая государственной облигации.

Спотовая кривая государственной облигации. Доходность к погашению (%) / Оставшийся срок погашения (годы).
Спотовая кривая государственной облигации. Доходность к погашению (%) / Оставшийся срок погашения (годы).

Эта спотовая кривая наклонена вверх и постепенно сглаживается для более длительных сроков погашения. Долгосрочные государственные облигации обычно имеют более высокую доходность, чем облигации с более коротким сроком. Эта модель типична в нормальных рыночных условиях.

Иногда спотовая кривая наклоняется вниз там, где более краткосрочная доходность выше, чем более долгосрочная доходность. Эта наклоненная вниз кривая называется инвертированной или перевернутой кривой доходности (англ. 'inverted yield curve'). Теории, которые пытаются объяснить форму кривой доходности и ее влияние на будущие условия финансового рынка, рассматриваются в следующих разделах.

Эта гипотетическая спотовая кривая идеально подходит для анализа структуры сроков погашения, потому что она наилучшим образом соответствует допущению о «разных вещах, которые одинаковы». Эти государственные облигации, по-видимому, имеют одинаковую валюту, кредитный риск, ликвидность и налоговый статус.

Самое важное, что у них нет риска реинвестирования купонов, потому что нет купонов для реинвестирования. Тем не менее, наиболее активно обращающиеся государственные и корпоративные облигации выплачивают купон. Следовательно, анализ структуры сроков погашения обычно основан на данных о ценах на государственные облигации, которые производят купонные платежи.

Эти купонные облигации могут иметь разную ликвидность и налоговый статус. Старые («выдержанные») облигации [т.е. обращающиеся на вторичном рынке], как правило, менее ликвидны, чем новая эмиссия долга [первичный рынок], потому что они удерживаются долгосрочными институциональным и розничными инвесторами.

Правительства выпускают новый долг со стандартными сроками погашения, например, 5-летние и 10-летние облигации. Текущая 6-летняя облигация может быть 10-летней облигацией, которая была выпущена 4 года назад.

Кроме того, из-за колебания процентных ставок более старые облигации оцениваются с дисконтом или премией к номиналу, что может привести к налоговым различиям. В некоторых странах прирост капитала имеет другой налоговый режим, чем убыток капитала и процентный доход.

Аналитики обычно используют только самые последние выпуски облигаций и наиболее активно обращающиеся государственные облигации для создания кривой доходности. Эти облигации имеют одинаковую ликвидность, и, поскольку они оцениваются ближе к номинальной стоимости, они имеют меньше налоговых эффектов.

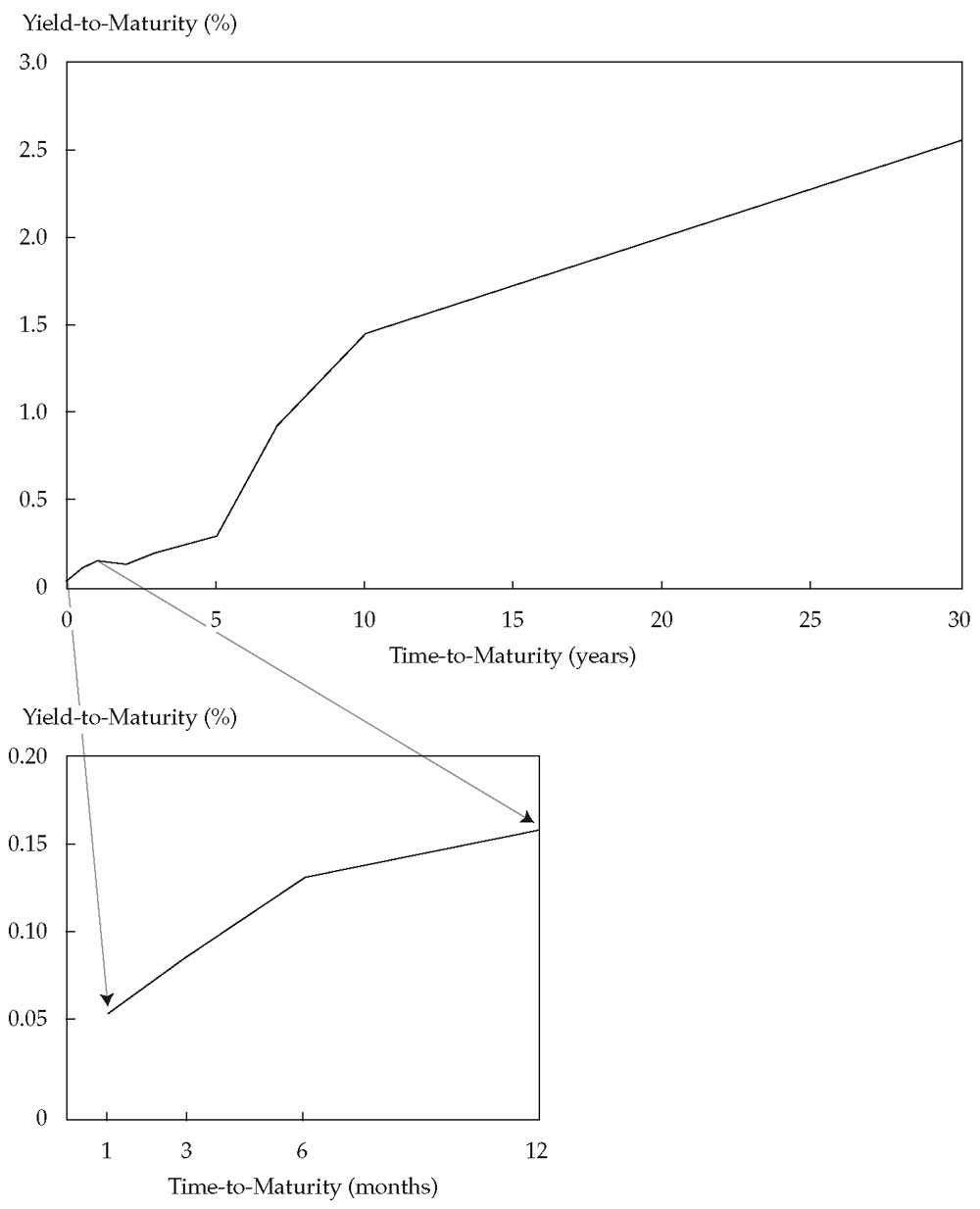
Проблема заключается в ограниченных данных для полного диапазона сроков погашения. Поэтому необходима интерполяция между наблюдаемыми кривыми доходности. Иллюстрация 6 показывает кривую доходности для 2-летних, 3-летних, 5-летних, 7-летних, 10-летних и 30-летних государственных облигаций с полугодовыми купонными выплатами. На кривой доходности купонных облигаций между этими точками используется прямая интерполяция.

Иллюстрация 6. Кривая доходности государственной облигации.

Кривая доходности государственной облигации. Доходность к погашению (%) / Оставшийся срок погашения (годы, месяцы).
Кривая доходности государственной облигации. Доходность к погашению (%) / Оставшийся срок погашения (годы, месяцы).

Иллюстрация 6 также включает доходность для краткосрочных государственных ценных бумаг, имеющих 1 месяц, со сроком до погашения 3 месяца, 6 месяцев и 12 месяцев. Хотя эти инструменты денежного рынка могут выпускаться и продаваться на основе ставки дисконтирования, они, как правило, представляются в отчетах как эквивалентная доходность по облигации.

Аналитику важно знать, были ли их ставки преобразованы в ту же периодичность, что и более долгосрочные государственные облигации. Если нет, то наблюдаемая кривая доходности может вводить в заблуждение, потому что количество периодов в году не совпадает.

В дополнение к кривой доходности по купонным облигациям и спотовой кривой по бескупонным облигациям, структуру сроков погашения можно оценивать с помощью кривой номинальной стоимости. Кривая номинальной стоимости или номинальная кривая (англ. 'par curve') - это последовательность ставок доходности к погашению, в которой каждая облигация оценивается по номинальной стоимости.

Предполагается, что облигации имеют одинаковую валюту, кредитный риск, ликвидность, налоговый статус и годовую доходность при одинаковой периодичности. Также предполагается, что в промежутках между датами выплаты купона фиксированная цена (но не полная цена) равна номинальной стоимости.

Номинальная кривая получена из спотовой кривой. На дату выплаты купона можно использовать следующую формулу для расчета ставки номинала с учетом данной последовательности спотовых ставок.

\( \begin{aligned} \dst
\def\PMT{{\rm PMT}}
100 = {\PMT \over (1+z_1)^1} + {\PMT \over (1+z_2)^2} + \ldots + {\PMT + 100 \over (1+z_N)^N}
\end{aligned} \)
(Формула 13)

Эта формула очень похожа на Формулу 2, за счет то го, что PV = FV = 100. Проблема заключается в том, чтобы вывести PMT алгебраически. Тогда PMT/100 будет равно ставке номинала за период.

Этот пример иллюстрирует расчет номинальной кривой с учетом спотовой кривой. Предположим, что спотовые ставки по государственным облигациям составляют 5.263% за 1 год, 5.616% за 2 года, 6.359% за 3 года и 7.008% за 4 года. Это эффективные годовые ставки.

1-летняя номинальная ставка составляет 5.263%.

\( \begin{aligned} \dst
\def\PMT{{\rm PMT}}
100 = {\PMT + 100 \over 1.05263^1} , \PMT = 5.263
\end{aligned} \)

2-летняя номинальная ставка составляет 5.606%.

\( \begin{aligned} \dst
\def\PMT{{\rm PMT}}
100 &= {\PMT \over 1.05263^1} + {\PMT + 100 \over 1.05616^2}, \\[1ex]
\PMT &= 5.606
\end{aligned} \)

3-летняя и 4-летняя номинальные ставки составляют 6.306% и 6.899% соответственно.

\( \begin{aligned} \dst
\def\PMT{{\rm PMT}}
100 &= {\PMT \over 1.05263^1} + {\PMT \over 1.05616^2} + {\PMT + 100 \over 1.06359^3}, \\[1ex]
\PMT &= 6.306
\end{aligned} \)

\( \begin{aligned} \dst
\def\PMT{{\rm PMT}}
100 &= {\PMT \over 1.05263^1} + {\PMT \over 1.05616^2} + {\PMT \over 1.06359^3}, \\[1ex]
&+ {\PMT + 100 \over 1.07008^4}, \\[1ex]
\PMT &= 6.899
\end{aligned} \)

До сих пор ценные бумаги с фиксированным доходом, которые мы рассматривали, были ценными бумагами денежного рынка. Ценные бумаги денежного рынка (англ. 'cash market securities') часто урегулируются в «тот же день», т.е. в день денежных расчетов.

Для других ценных бумаг есть временная разница между датой торгов и датой урегулирования.

Например, если государственные облигации торгуются на основе схемы T + 1, есть 1-дневная разница между датой торгов и датой урегулирования. Если корпоративная облигация торгуется на основе схемы T + 3, продавец предоставляет облигацию, а покупатель производит оплату в течение 3-х рабочих дней.

Денежные рынки также называют спотовыми или срочными рынками (англ. 'spot markets'), что может ввести в заблуждение, потому что термин «спотовая ставка» (spot rate) может иметь два значения. Он может означать «ставку по облигации, обращающейся на спотовом или денежном рынке». Он также может означать «доходность по бескупонной облигации», что является смыслом спотовой ставки, используемым в этом чтении.

Форвардный рынок (англ. 'forward market') предназначен для обеспечения будущей поставки, за рамками обычного периода урегулирования на денежном рынке. Договоренность о сроках сделки соответствует дате торгов, но передача ценной бумаги и ее оплата откладываются на будущую дату.

Форвардная ставка (англ. 'forward rate') - это процентная ставка по инструменту рынка облигаций или денежного рынка, который обращается на форвардном рынке. Например, предположим, что на денежном рынке 5-летняя бескупонная облигация оценивается в 81 на 100 номинальной стоимости. Ее доходность к погашению составляет 4.2592% на полугодовой основе.

\( \begin{aligned}
&81 = {100 \over (1+r)^{10}}, \\[1ex]
&r = 0.021296, \times 2 = 0.042592
\end{aligned} \)

Предположим, что дилер соглашается предоставить 5-летнюю облигацию через 2 года в будущем по цене 75 на 100 номинальной стоимости. Кредитный риск, ликвидность и налоговый статус этой облигации, обращающейся на форвардном рынке, такие же, как и на денежном рынке.

Форвардная ставка составляет 5.8372%.

\( \begin{aligned}
&75 = {100 \over (1+r)^{10}}, \\[1ex]
&r = 0.029186, \times 2 = 0.058372
\end{aligned} \)

Важно понимать нотацию (условное обозначение) форвардных ставок. Хотя авторы финансовых учебников используют различные обозначения, наиболее распространенной рыночной практикой является обозначение «2y5y». Оно произносится как «два года в пятилетней ставке» (the two-year into five-year rate) или просто «the 2's, 5's».

Смысл этой нотации в том, что первое число (2 года) относится к продолжительности форвардного периода в годах с сегодняшнего дня, а второе число (5 лет) относится к тенору облигации. Тенор - это оставшийся срок до погашения облигации (или производного договора).

Таким образом, 5.8372% - это форвардная ставка в нотации «2y5y» для бескупонной облигации, т.е. 5-летняя доходность через 2 года в будущем. Обратите внимание, что облигация, которая станет 5-летней через 2 года, в настоящее время имеет 7 лет до погашения.

На денежном рынке форвардная ставка обычно относится к месяцам. Например, аналитик может запросить форвардную ставку Euribor «1m6m», которая соответствует 6-месячной ставке Euribor через 1 месяц в будущем.

Подразумеваемая форвардная ставка (англ. 'implied forward rate'), также известная как форвардная доходность (англ. 'forward yield'), рассчитывается по спотовым ставкам.

Подразумеваемая форвардная ставка - это ставка безубыточного реинвестирования. Она связывает доходность инвестиций в краткосрочную бескупонную облигацию с доходностью инвестиций в более долгосрочную бескупонную облигацию.

Предположим, что срок погашения более краткосрочной облигации наступает через A периодов, а срок погашения более долгосрочной облигации наступает через B периодов. Доходность к погашению за период по этим облигациям обозначается как \(z_A\) и \(z_B\).

Подразумеваемая форвардная ставка за временной промежуток между периодом A и периодом B обозначается как \({\rm IFR}_{A, B-A}. Это форвардная ставка по ценной бумаге, которая начинается в период A и заканчивается в период B.

Ее тенор - это количество периодов \(B - A\).

Формула 14 является общей формулой, отражающей взаимосвязь между двумя спотовыми ставками и подразумеваемой форвардной ставкой.

\( \begin{aligned} \dst
\def\IFR{\rm IFR}
(1+z_A)^A \times (1+ \IFR_{A,B-A})^{B-A} = (1+z_B)^B
\end{aligned} \)
(Формула 14)

Предположим, что доходность к погашению по 3-летней и 4-летней бескупонным облигациям составляет 3.65% и 4.18% на полугодовой основе, соответственно. Аналитик хочет выяснить подразумеваемую форвардную ставку «3y1y», что означает подразумеваемую 1-летнюю форвардную доходность через 3 года в будущем.

Следовательно, \(A = 6\) (периодов), \(B = 8\) (периодов), \(B - A = 2\) (периода), \(Z_6 = 0.0365/2 \) (за период) и \( Z_8 = 0.0418/2 \) (за период).

\( \dst
\def\IFR{\rm IFR}
\left(1 + {0.0365 \over 2} \right)^6 \times (1 + \IFR_{6,2})^2
= \left(1 + {0.0418 \over 2} \right)^8
\)

\( \dst
\def\IFR{\rm IFR}
\IFR_{6,2} = 0.02889, \ \times 2 = 0.05778
\)

Подразумеваемая форвардная доходность «3y1y» составляет 5.778%, что является годовой ставкой с периодичностью 2.

Формулу 14 можно использовать для построения форвардной кривой. Форвардная кривая (англ. 'forward curve') - это последовательность форвардных ставок, каждая из которых имеет одинаковый временной шаг. Эти форвардные ставки можно наблюдать в операциях на рынке производных инструментов.

Форвардные ставки часто возникают в результате операций на рынке денежных средств. Иллюстрация 7 показывает форвардную кривую, которая рассчитывается на основе спотовой кривой государственной облигации, показанной в Иллюстрации 5. Это 1-летние форвардные ставки, указанные на полугодовой основе.

Иллюстрация 7. Спотовая кривая и форвардная кривая по государственной облигации.

Спотовая кривая и форвардная кривая по государственной облигации.
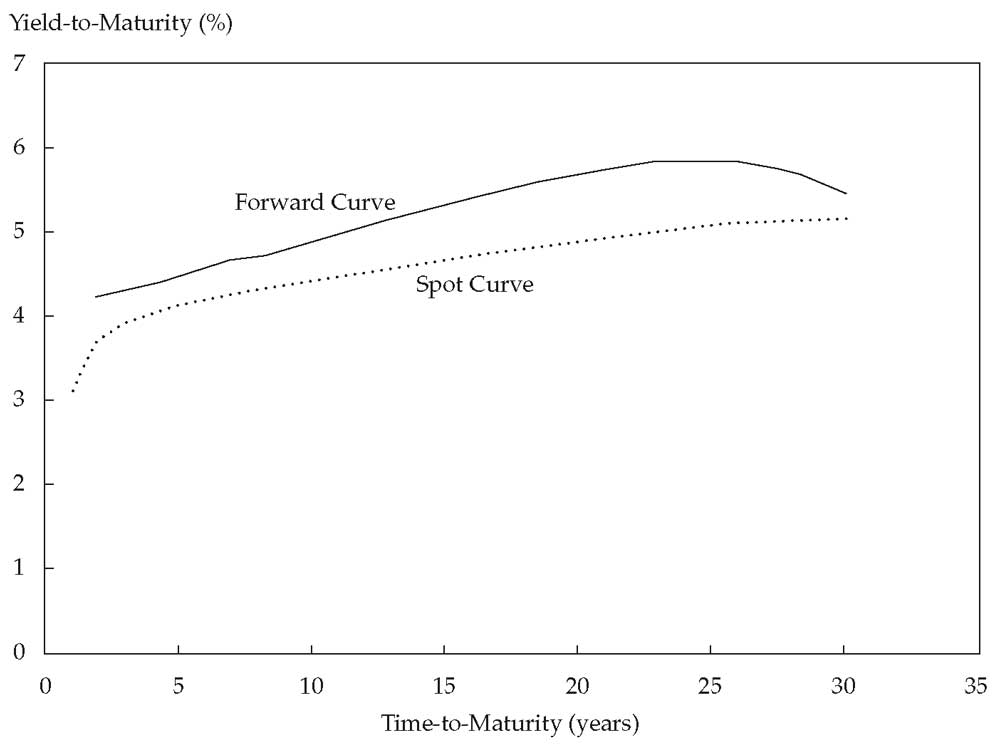
Спотовая кривая и форвардная кривая по государственной облигации.

Форвардную ставку можно интерпретировать как дополнительную или предельную доходность, поскольку она увеличивает оставшийся до погашения срок на дополнительный период времени.

Предположим, что инвестор рассматривает 4-летний инвестиционный горизонт и выбирает между покупкой 3-летней бескупонной облигацией с доходностью 3.65% и 4-летней бескупонной облигацией с доходностью 4.18%.

Дополнительная или предельная доходность за 4-й год составляет 5.778%, что является подразумеваемой форвардной ставкой «3y1y». Если мнение инвестора о будущей доходности облигаций заключается в том, что 1-летняя доходность через 3 года, вероятно, составит менее 5.778%, инвестор может предпочесть купить 4-летнюю облигацию.

Однако, если инвестор считает, что 1-летняя доходность будет больше, чем подразумеваемая форвардная ставка, инвестор может предпочесть 3-летнюю облигацию и возможность реинвестировать по более высокой ставке.

Это объясняет, почему подразумеваемая форвардная ставка является ставкой безубыточного реинвестирования. Подразумеваемые форвардные ставки очень полезны как для инвесторов, так и для эмитентов облигаций при принятии решений о сроках погашения.

Пример (11) расчета форвардных ставок.

Предположим, что инвестор наблюдает следующие цены и доходность к погашению по бескупонным государственным облигациям:

Срок погашения

Цена

Доходность к погашению

1 год

97.50

2.548%

2 года

94.25

2.983%

3 года

91.75

2.891%

Цены указаны на 100 д.е. номинальной стоимости. Доходность к погашению указана на полугодовой основе.

1. Рассчитайте подразумеваемые форвардные ставки «1y1y» и «2y1y», указанные на полугодовой основе.

2. Инвестор рассматривает 3-летний инвестиционный горизонт и выбирает между:

  • (1) покупкой 2-летней бескупонной облигации и реинвестированием в другую 1-летнюю бескупонную облигацию через 2 года и
  • (2) покупкой и удержанием до погашения 3-летней бескупонной облигации.

Инвестор решает купить 2-летнюю облигацию. Основываясь на этом решении, что из нижеперечисленного является минимальной доходностью к погашению, которую инвестор ожидает по 1-летней бескупонной облигации через 2 года?

  1. 2.548%
  2. 2.707%
  3. 2.983%

Решение для части 1:

Подразумеваемая форвардная ставка «1y1y» составляет 3.419%. В Формулу 14 подставляем \(A = 2\) (периода), \(B = 4\) (периода), \(B - A = 2\) (периода), \(z_2 = 0.02548/2 \) (за период) и \(z_4 = 0.02983/2 \) (за период).

\( \begin{aligned}
\def\IFR{{\rm IFR}}
&\left( 1 + {0.02548 \over 2} \right)^2 \times (1 + \IFR_{2,2})^2 =
\left( 1 + {0.02983 \over 2} \right)^4, \\[1ex]
&\IFR_{2,2} = 0.017095, \ \times 2 = 0.03419
\end{aligned} \)

Подразумеваемая форвардная ставка «2y1y» составляет 2.707%. В Формулу 14 подставляем \(A = 4\) (периода), \(B = 6\) (периода), \(B - A = 2\) (периода), \(z_4 = 0.02983/2 \) (за период) и \(z_6 = 0.02891/2 \) (за период).

\( \begin{aligned}
\def\IFR{{\rm IFR}}
&\left( 1 + {0.02983 \over 2} \right)^4 \times (1 + \IFR_{4,2})^2 =
\left( 1 + {0.02891 \over 2} \right)^6, \\[1ex]
&\IFR_{4,2} = 0.013536, \ \times 2 = 0.02707
\end{aligned} \)

Решение для части 2:

Ответ B правильный. Инвестор предполагает, что 1-летняя доходность через 2 года будет больше или равна 2.707%.

Подразумеваемая форвардная ставка «2y1y» 2.707% - это ставка безубыточного реинвестирования. Если инвестор ожидает, что 1-летняя ставка через 2 года будет меньше, чем эта подразумеваемая форвардная ставка, от предпочтет купить 3-летнюю бескупонную облигацию.

Если инвестор ожидает, что 1-летняя ставка через 2 года превысит 2.707%, он может предпочесть купить 2-летнюю бескупонную облигацию и реинвестировать денежный поток.

Форвардная кривая имеет множество применений в анализе фиксированного дохода. Форвардные ставки используются для принятия решений о выборе сроков погашения. Они используются для выявления арбитражных возможностей между операциями на денежном рынке облигаций и на рынках деривативов.

Форвардные ставки важны при оценке деривативов, особенно процентных свопов и опционов. Эти применения форвардной кривой более подробно рассматриваются в следующих разделах.

Форвардные ставки могут использоваться для оценки ценных бумаг с фиксированным доходом таким же образом, как и спотовые ставки, поскольку они взаимосвязаны. Спотовую кривую можно рассчитать на основе форвардной кривой, а форвардную кривую - на основе спотовой кривой.

Любую кривую можно использовать для оценки облигаций с фиксированной ставкой. Следующий пример иллюстрирует это.

Предположим, что текущая форвардная кривая для 1-летних ставок выглядит следующим образом:

Временной период

Форвардная ставка

0y1y

1.88%

1y1y

2.77%

2y1y

3.54%

3y1y

4.12%

Эти годовые ставки имеют периодичность 1. Это эффективные годовые ставки. Первая ставка, «0y1y», является 1-летней спотовой ставкой. Остальные - 1-летние форвардные ставки. Учитывая это, спотовую кривую можно рассчитать как среднее геометрическое значение форвардных ставок.

2-летняя подразумеваемая спотовая ставка составляет 2.3240%.

\( (1.0188 \times 1.0277) = (1 + z_2)^2, \ z_2 = 0.023240 \)

Ниже приведены уравнения для 3-летних и 4-летних подразумеваемых спотовых ставок.

\( (1.0188 \times 1.0277 \times 1.0354) = (1 + z_3)^3 \),

\( z_3 = 0.027278 \)

\( (1.0188 \times 1.0277 \times 1.0354 \times 1.0412) = (1 + z_4)^4 \),

\( z_4 = 0.030741 \)

3-летняя подразумеваемая спотовая ставка составляет 2.7278%, а 4-летняя спотовая ставка составляет 3.0741%.

Предположим, что аналитик должен оценить 4-летнюю облигацию с доходностью 3.75% и годовым купоном, которая имеет те же риски, что и облигации, использованные для построения форвардной кривой.

Используя подразумеваемые спотовые ставки, можно оценить, что стоимость облигации составляет 102.637 на 100 номинальной стоимости.

\( \begin{aligned} \dst
{3.75 \over 1.0188^1} &+ {3.75 \over 1.023240^2} + {3.75 \over 1.027278^3} \\[1ex]
&+ {103.75 \over 1.030741^4} = 102.637
\end{aligned} \)

Облигацию также можно оценить с использованием форвардной кривой.

\( \begin{aligned} \dst
{3.75 \over 1.0188} &+ {3.75 \over 1.0188 \times 1.0277} + {3.75 \over 1.0188 \times 1.0277 \times 1.0354} \\[1ex]
&+ {103.75 \over 1.0188 \times 1.0277 \times 1.0354 \times 1.0412} = 102.637
\end{aligned} \)