Чтобы понять значение вероятности в инвестиционном контексте, нам необходимо различать два типа вероятности: безусловную и условную.

Как безусловные, так и условные вероятности удовлетворяют приведенному ранее определению вероятности, но они рассчитываются или оцениваются по-разному и имеют разные интерпретации. Они дают ответы на разные вопросы.

Вероятность в ответе на простой вопрос «Какова вероятность этого события \(A\)?» - это безусловная вероятность (англ. 'unconditional probability' или 'marginal probability'), обозначаемая \(P(A)\).

При анализе вероятностей, представленных в таблицах, безусловные вероятности обычно выводятся в конце или на полях таблицы, отсюда и термин marginal probability, от англ. 'margin' - поле страницы.

Из-за возможной путаницы с тем, что термин margin используется в экономике в другом смысле (например, как маржинальный применительно к прибыли), лучше использовать термин 'unconditional probability'.

Что такое безусловная вероятность?

Рассмотрим вопрос: «Какова вероятность того, что акция принесет доход выше безрисковой ставки (событие \(A\))»?

Ответ - это безусловная вероятность, которую можно рассматривать как соотношение двух величин.

Числитель - это сумма вероятностей доходности акций выше безрисковой ставки. Предположим, что эта сумма 0.70. Знаменатель равен 1, т.е. сумме вероятностей всех возможных ставок доходности.

Ответ на вопрос:

\(P(A) = 0.70\)

Что такое условная вероятность?

Сравните вопрос «Какова вероятность события \(A\)?» с вопросом «Какова вероятность события \(A\), учитывая, что событие \(B\) произошло?»

Вероятность в ответе на этот последний вопрос является условной вероятностью (англ. 'conditional probability'), обозначаемой как \( P(A|B) \) (читается как: «вероятность \(A\) при условии \(B\)»).

Предположим, мы хотим знать вероятность того, что акция принесет доход выше безрисковой ставки (событие \(A\)), при условии, что акция принесет положительный доход (событие \(B\)). Фразой «при условии» мы ограничиваем исход доходностью более 0%.

Условная вероятность рассчитывается как отношение двух величин.

Числитель - это сумма вероятностей доходности акций выше безрисковой ставки; в данном конкретном случае числитель такой же, как и в случае с безусловной вероятностью: 0.70.

Знаменатель, однако, изменяется от 1 до суммы вероятностей для всех исходов (ставок доходности) выше 0%.

Предположим, что знаменатель равен 0.80, что больше, чем 0.70, поскольку доходность от 0 до безрисковой ставки имеет некоторую положительную вероятность возникновения.

Тогда,

\( P(A | B) = 0.70/0.80 = 0.875 \)

Если мы наблюдаем, что акция приносит положительный доход, то вероятность доходности выше безрисковой ставки будет больше, чем безусловная вероятность, то есть вероятность события, не сопровождаемая никакой другой информацией. Результат интуитивно понятен.

В этом примере условная вероятность больше, чем безусловная вероятность. Тем не менее, в зависимости от фактов условная вероятность события может быть больше, равна или меньше безусловной вероятности.

Например, вероятность того, что акция принесет доход выше безрисковой ставки, при условии того, что акция принесет отрицательный доход, равна 0.

Уточним еще раз:

  • Безусловная вероятность - это вероятность события без каких-либо ограничений; она может даже рассматриваться как отдельная вероятность.
  • Условная вероятность, напротив, является вероятностью события, с учетом того, что произошло другое событие.

При обсуждении подходов к расчету вероятности мы дали одну эмпирическую оценку вероятности того, что изменение дивидендов является уменьшением дивидендов. Эта вероятность была безусловной вероятностью.

Учитывая дополнительную информацию о характеристиках компании, может ли инвестор уточнить эту оценку?

Инвесторы постоянно ищут информационное преимущество, которое поможет улучшить их прогнозы. С математической точки зрения они пытаются сформулировать свое видение будущего, используя вероятности, обусловленные соответствующей информацией или событиями. Инвесторы не игнорируют полезную информацию; они корректируют свои вероятности, чтобы учесть ее.

Таким образом, концепции условной вероятности, а также связанные с ними концепции, обсуждаемые далее, чрезвычайно важны в инвестиционном анализе и анализе финансовых рынков.

Что такое совместная вероятность?

Чтобы сформулировать точное определение условной вероятности, нам сначала нужно ввести понятие совместной вероятности (англ. 'joint probability').

Предположим, мы задаем вопрос: «Какова вероятность того, что произойдет и событие \(A\), и событие \(B\)?». Ответом на этот вопрос является совместная вероятность, обозначаемая \( P(AB) \) (читается как: «вероятность событий \(A\) и \(B\)»).

Если мы думаем о вероятности \(A\) и вероятности \(B\) как о наборах данных, построенных из результатов одной или нескольких случайных величин, совместная вероятность \(A\) и \(B\) является суммой вероятностей общих для них результатов.

Например, рассмотрим два события:

  • акция приносит доход выше безрисковой ставки \((A)\), а
  • акция приносит положительный доход \((B)\).

Результаты \(A\) содержатся в подмножестве результатов \(B\), поэтому \(P(AB)\)\) равно \(P(A)\).

Теперь мы можем сформулировать формальное определение условной вероятности, которое обеспечивает формулу для ее вычисления.

Определение условной вероятности.

Условная вероятность \(A\) при условии события \(B\) равна общей вероятности \(A\) и \(B\), деленной на вероятность \(B\) (предполагается, что она не равна 0).

\( \large P(A|B) = P(AB)/P(B), P(B) \neq 0 \) (Формула 1)

Иногда мы знаем условную вероятность \(P (A|B)\) и хотим знать общую вероятность \(P(AB)\). Мы можем получить общую вероятность из следующего правила умножения для вероятностей, которое выведено из Формулы 1.

Правило умножения для вероятности.

Совместная вероятность \(A\) и \(B\) может быть выражена как:

\( \large P(AB) = P(A|B)P(B) \) (Формула 2)

Пример (2). Условная вероятность и предсказуемость финансовых результатов взаимного фонда.

Французский исследователь Vidal-Garcia (2013) изучил, прогнозируют ли исторические показатели будущие результаты для выборки взаимных фондов, включающей 1050 активно управляемых фондов акций в 6 европейских странах в период с 1988 по 2010 год.

Фонды были классифицированы по 9 инвестиционным стилям на основе сочетаний инвестиционной направленности (рост, смешивание и стоимость) и рыночной капитализации фонда (малая, средняя и большая капитализация).

Один из подходов, использованных Vidal-Garcia, заключался в расчете годовой доходности, скорректированной по контрольным показателям каждого фонда, путем вычитания контрольной доходности из годовой доходности фонда.

В качестве ориентиров использовались индексы стиля MSCI (Morgan Stanley Capital International).

Для каждого инвестиционного стиля фонда в каждой стране фонды классифицировались как выигрышные или проигрышные в течение каждого из двух последовательных лет.

Первые 50% фондов по доходности, скорректированной по контрольным показателям, за данный год были названы выигрышными; остальные 50% были названы проигрышными.

Выдержка из результатов исследования для 135 французских фондов, классифицируемых как крупные фонды, приведена в Таблице 2. Она показывает процентную долю тех фондов, которые были выигрышными в течение 2 лет подряд, выигрышными в течение 1 года, а также сначала проигрышными, а затем выигрышными, и проигрышными в оба года.

Например, ячейка таблицы Выигрышный (год 2) / Выигрышный (год 1) показывает, что 65,5% фондов, выигрышных в 1-м году, также были выигрышными во 2-м году. Обратите внимание, что четыре значения в таблице можно рассматривать как условные вероятности.

Таблица 2. Постоянство доходности
крупных фондов во Франции: с 1988 по 2010 гг.

Выигрышный
(год 2)

Проигрышный
(год 2)

Выигрышный (год 1)

65.5%

34.5%

Проигрышный (год 1)

15.5%

84.5%

Источник: Vidal-Garcia (2013).

На основании данных Таблицы 2 сделайте следующее:

  1. Укажите четыре события, необходимые для определения четырех условных вероятностей.
  2. Сформулируйте четыре значения таблицы как условные вероятности, используя форму P(событие | событие) = значение.
  3. Определите, являются ли условные вероятности в части 2 эмпирическими, априорными или субъективными вероятностями?
  4. Используя информацию, приведенную в таблице, рассчитайте вероятность того, что фонд потерпел неудачу как в 1-м, так и в 2-м годах. (Обратите внимание, что, поскольку 50% фондов классифицируются как проигрышные в каждом году, безусловная вероятность того, что фонд будет классифицирован как проигрышный в любом году составляет 0.5).

Решение для части 1:

Четыре события, необходимые для определения условных вероятностей:

  • Фонд - выигрышный в 1 году
  • Фонд - проигрышный в 1 году
  • Фонд - проигрышный во 2 году
  • Фонд - выигрышный во 2 году

Решение для части 2:

Из ряда 1:

  • P(Фонд - выигрышный во 2 году | Фонд - выигрышный в 1 году) = 0.655
  • P(Фонд - проигрышный во 2 году | Фонд - выигрышный в 1 году) = 0.345

Из ряда 2:

  • P(Фонд - выигрышный во 2 году | Фонд - проигрышный в 1 году) = 0.155
  • P(Фонд - проигрышный во 2 году | Фонд - проигрышный в 1 году) = 0.845

Решение для части 3:

Эти вероятности рассчитываются на основе данных, поэтому они являются эмпирическими вероятностями.

Решение для части 4:

Расчетная вероятность составляет 0.423.

Если событие А означает, что фонд является проигрышным во 2-м года, а событие В - то, что фонд является проигрышным в 1-м года, то событие AB означает, что фонд является проигравшим как в 1-м, так и в 2-м году.

Берем соответствующие значения из Таблицы 2:

\( P(A|B) = 0.845\) и \(P(B) = 0.50\)

Таким образом, используя Формулу 2, мы находим:

\( P(AB) = P(A|B)P(B) = 0.845(0.50) = 0.4225\)

или вероятность приблизительно равную 0.423.

Формула 2 гласит, что совместная вероятность событий \(A\) и \(B\) равна вероятности \(A\), при условии \(B\), умноженной на вероятность \(B\).

Поскольку \( P(AB) = P(BA) \), выражение \( P(AB) = P(BA) = P(B|A)P(A) \) эквивалентно Формуле 2.

Когда у нас есть два события, \(A\) и \(B\) , которые нас интересуют, мы часто хотим знать вероятность того, что произойдет \(A\) или \(B\) . Здесь слово «или» является включающим, что означает, что происходит либо \(A\), либо \(B\) , либо \(A\) и \(B\) .

Иными словами, вероятность \(A\) или \(B\) - это вероятность того, что произойдет хотя бы одно из двух событий. Такие вероятности рассчитывается с использованием правила сложения для вероятностей.

Правило сложения для вероятностей.

При данных событиях \(A\) и \(B\) вероятность того, что произойдет \(A\) или \(B\) , или что произойдут оба события, равна вероятности того, что произойдет событие \(A\), плюс вероятность того, что произойдет событие \(B\) , минус вероятность того, что произойдут \(A\) и \(B\) .

\( \large P(A \small{\text{ или }} \large B) = P(A) + P(B) - P(AB)  \) (Формула 3)

Если мы рассматриваем отдельные вероятности \(A\) и \(B\) как наборы данных, построенные из результатов одной или нескольких случайных величин, первый шаг в вычислении вероятности \(A\) или \(B\) состоит в суммировании вероятностей результатов \(A\) для получения \(P(A)\).

Если \(A\) и \(B\) имеют какие-либо общие результаты, то, если бы мы теперь добавили \(P(B)\) к \(P(A)\), мы бы посчитали вдвое больше вероятностей этих общих результатов. Таким образом, мы добавляем к \(P(A)\) величину \([P(B) - P(AB)]\), которая является вероятностью результатов \(B\) за вычетом вероятности любых результатов, уже подсчитанных при вычислении \(P(A)\).

Рисунок 1 иллюстрирует этот процесс; мы избегаем двойного подсчета результатов на пересечении \(A\) и \(B\) , вычитая P(AB).

В качестве примера расчета,

если \( P(A) = 0.50, P(B) = 0.40\), и \(P(AB) = 0.20\),
то \( P(A \text{ или } B) = 0.50 + 0.40 - 0.20 = 0.70\).

Только в случае если два события \(A\) и \(B\) являются взаимоисключающими, \( P(AB) \) будет равно 0.

Было бы правильно заявить, что \( P(A \text{ или } B) = P(A) + P(B) \).

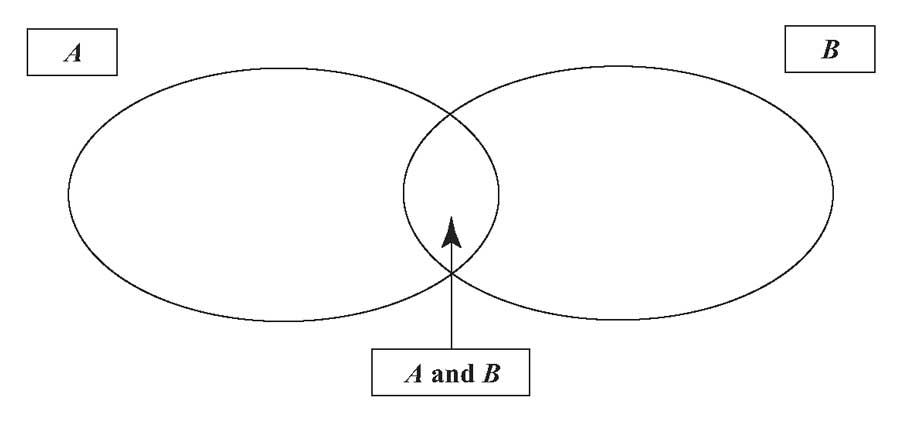Рисунок 1. Правило сложения для вероятностей. Рисунок 1. Правило сложения для вероятностей.

Следующий пример показывает, сколько полезной информации можно получить, используя несколько правил вероятности, представленных на данный момент.

Пример (3) вероятности выполнения заявки на покупку акций с ограничением цены.

У вас есть две неисполненных лимитных заявки на одну и ту же акцию.

Лимитная заявка на покупку акций по заявленной цене (или заявка с ограничением цены, от англ. 'limit order') - это заявка на покупку по указанной цене или ниже.

См. также:

CFA - Биржевые заявки: инструкции исполнения заявок.

Ряд поставщиков, в том числе используемая вами интернет-служба, предоставляют предполагаемую вероятность того, что лимитная заявка будет исполнена в течение установленного периода времени, с учетом текущей цены акций и лимита цены.

Одна лимитная заявка (Заявка 2) была размещена по цене $10. Вероятность того, что она будет исполнена в течение одного часа, составляет 0.35.

Вторая лимитная заявка (Заявка 2) была размещена по цене $9.75; вероятность ее исполнения в течение одного часа составляет 0.25.

  1. Какова вероятность того, что Заявка 1 или Заявка 2 будут исполнены?
  2. Какова вероятность того, что Заявка 2 будет исполнена, при условии, что Заявка 1 также будет исполнена?

Решение для части 1:

Вероятность составляет 0.35.

Даны две вероятности: Р(Заявка 1 исполнена) = 0.35 и Р(Заявка 2 исполнене) = 0.25.

Обратите внимание, что если Заявка 2 исполнена, то, несомненно, что Заявка 1 также исполнена, потому что цена должна превысить $10, что больше $9.75.

Таким образом,

Р(Заявка 1 исполнена | Заявка 2 исполнена) = 1

а также,

Р(Заявка 1 исполнена И Заявка 2 исполнена) =
Р(Заявка 1 исполнена | Заявка 2 исполнена)
\(\times\) P(Заявка 2 исполнена) =
= 1(0.25) = 0.25

Чтобы ответить на вопрос, мы используем правило сложения для вероятностей:

Р(Заявка 1 исполнена ИЛИ Заявка 2 исполнена) =
Р(Заявка 1 исполнена) + Р(Заявка 2 исполнена) - Р(Заявка 1 исполнена И Заявка 2 исполнена) =
= 0.35 + 0.25 - 0.25 = 0.35

Обратите внимание, что результаты, для которых Заявка 2 исполнена, являются подмножеством результатов, для которых исполнена Заявка 1.

Если вы посчитаете вероятность того, что Заявка 1 исполнена, то также посчитаете вероятность того, что исполнена Заявка 2.

Следовательно, вероятностью того, что Заявка 1 исполнена, будет 0.35.

Решение для части 2:

Если Заявка 1 исполняется, вероятность исполнения Заявки 2 составляет 0.714.

В решении для части 1 вы обнаружили, что Р(Заявка 1 исполнена И Заявка 2 исполнена) = 1(0.25) = 0.25.

Эквивалентный способ выразить эту совместную вероятность будет полезен и здесь:

Р(Заявка 1 исполнена И Заявка 2 исполнена) = 0.25 = Р(Заявка 2 исполнена | Заявка 1 исполнена) \(\times\) P(Заявка 1 исполнена)

Поскольку известно, что P(Заявка 1 исполнена) = 0.35, у вас есть одно уравнение с одним неизвестным:

0.25 = Р(Заявка 2 исполнена | Заявка 1 исполнена) (0.35)

Вы определяете, что

Р(Заявка 2 исполнена | Заявка 1 исполнена) = 0.25/0.35 = 5/7 или примерно 0.714.

Вы также можете использовать Формулу 1, чтобы такое же решение.