CFA - Анализ вариации простой линейной регрессии
Рассмотрим разложение общей суммы квадратов регрессионной модели на компоненты, а также расчет и интерпретацию коэффициента детерминации, F-статистику и стандартную ошибку простой линейной регрессии, - в рамках изучения количественных методов по программе CFA (Уровень II).
Модель простой линейной регрессии иногда довольно хорошо описывает зависимость между двумя переменными, но иногда это не так.
Финансовые аналитики должны различать эти два случая для эффективного использования регрессионного анализа.
Помните, что наша цель - объяснить изменение зависимой переменной. Итак, насколько хорошо мы достигли этой цели, учитывая наш выбор независимой переменной?
Разложение общей суммы квадратов на компоненты.
Мы начинаем с получения общей или полной суммы квадратов (SST, sum of squares total), а затем раскладываем ее на две части: сумму квадратов ошибки или остатков (SSE, sum of squares error) и сумму квадратов регрессии.
Сумма квадратов регрессии или объясненная сумма квадратов (SSR, sum of squares regression) - это сумма квадратов разностей между прогнозируемым значением зависимой переменной \(\hat Y_i\), полученным на основе линии регрессии, и средним значением зависимой переменной \( \overline Y \):
\( \Large \sum^n_{i=1} (\hat Y_i - \overline Y)^2 \) (9)
Мы уже определили общую сумму квадратов, которая представляет собой общую вариацию (дисперсию) в \(Y\), а также сумму квадратов ошибки, которая представляет собой необъясненную вариацию (дисперсию) в \(Y\).
Обратите внимание, что сумма квадратов регрессии - это объясненная вариация в \(Y\).
Таким образом, как показано в Иллюстрации 19, SST = SSR + SSE, что означает, что общая вариация в \(Y\) равна сумме объясненной вариации в \(Y\) и необъясненной вариации в \(Y\).
Иллюстрация 19. Разложение вариации (дисперсии) зависимой переменной.
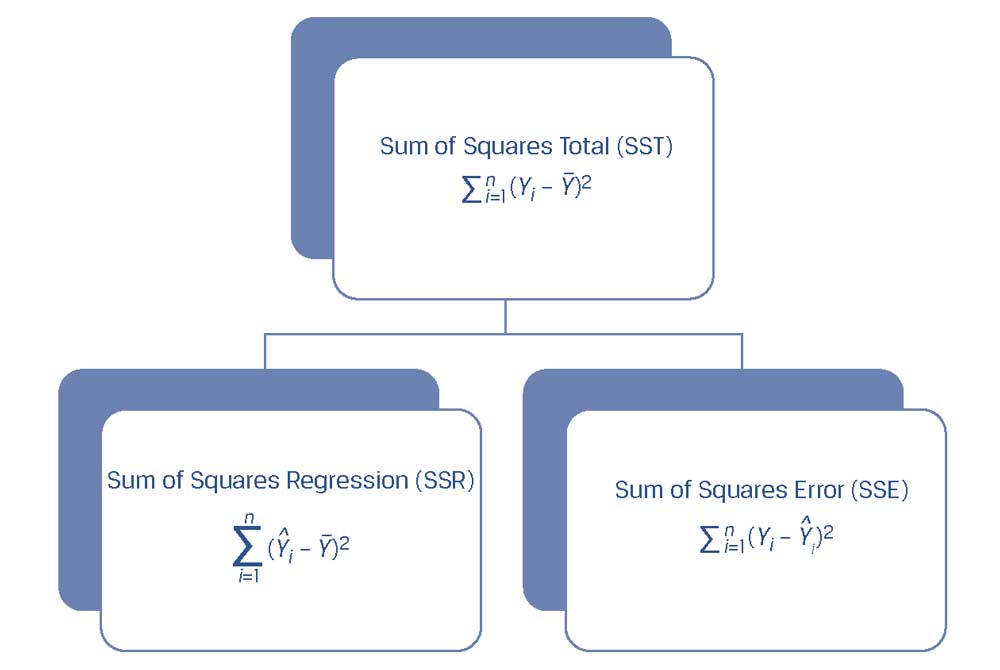
Разложение вариации (дисперсии) зависимой переменной.
Мы покажем разложение формулы общей суммы на примере регрессии ROA, представленной в Иллюстрации 20. Общая вариация ROA, которую мы хотим объяснить (SST), составляет 239.50.
Это число включает в себя необъясненную вариацию (SSE), 47.88, а также объясненную вариацию (SSR), 191.63. Эти суммы квадратов являются важными исходными данными для анализа правильности построения регрессии.
Далее мы рассмотрим показатели, с помощью которых проводится оценивается соответствие построенной регрессии исходным данным.
Иллюстрация 20. Разложение общей суммы квадратов для модели регрессии ROA.
|
Компания |
ROA \((Y_i)\) |
CAPEX \((X_i)\) |
Прогнозируемая ROA \((\hat Y)\) |
Вариация, которую нужно объяснить \((Y_i - \overline Y)^2 \) |
Необъясненная вариация \((Y_i - \hat Y)^2 \) |
Объясненная вариация \((\hat Y_i - \overline Y)^2 \) |
|
A |
6.0 |
0.7 |
5.750 |
42.25 |
0.063 |
45.563 |
|
B |
4.0 |
0.4 |
5.375 |
72.25 |
1.891 |
50.766 |
|
C |
15.0 |
5.0 |
11.125 |
6.25 |
15.016 |
1.891 |
|
D |
20.0 |
10.0 |
17.375 |
56.25 |
6.891 |
23.766 |
|
E |
10.0 |
8.0 |
14.875 |
6.25 |
23.766 |
5.641 |
|
F |
20.0 |
12.5 |
20.500 |
56.25 |
0.250 |
64.000 |
|
239.50 |
47.88 |
191.625 |
||||
|
Среднее значение |
12.50 |
- Общая сумма квадратов = 239.50.
- Сумма квадратов ошибок = 47,88.
- Сумма квадратов регрессии = 191,63.
Показатели правильности построения (степени согласия) регрессии.
Есть несколько показателей, которые мы можем использовать для оценки степени согласия (goodness of fit), то есть того, насколько хорошо регрессионная модель подходит к исходным данным.
К этим показателям относятся коэффициент детерминации, F-статистика для проверки соответствия регрессионной модели и стандартная ошибка регрессии.
Коэффициент детерминации (coefficient of determination), который также называют R-квадратом или \(R^2\), представляет собой процентное выражение дисперсии зависимой переменной, которая объясняется независимой переменной:
\( \dst \large
\text{Коэффициент детерминации} = \large {
\text{Сумма квадратов регрессии} \over \text{Общая сумма квадратов}
} \)
\( \dst \large
\text{Коэффициент детерминации} = \large \dst {
\sum^n_{i=1} (\hat Y_i - \overline Y)^2 \over \sum^n_{i=1} (Y_i - \overline Y)^2
} \) (10)
Значение коэффициента детерминации колеблется от 0% до 100%.
В нашем примере с ROA коэффициент детерминации составляет 191.625 + 239.50, или 0.8001 (80.01%). Поэтому 80.01% является вариацией ROA, объясненной CAPEX.
В простой линейной регрессии квадрат парной корреляции равен коэффициенту детерминации:
\( \dst \large
r^2 = \dst { \sum^n_{i=1} (\hat Y_i - \overline Y)^2 \over
\sum^n_{i=1} (Y_i - \overline Y)^2 } = R^2
\)
В нашем анализе регрессии ROA, который мы провели ранее, \(r\) = 0.8945, поэтому теперь мы видим, что \(r^2\) действительно равен коэффициенту детерминации \((R^2)\), поскольку \( (0.8945)^2 = 0.8001 \).
Коэффициент детерминации - это часть вариации (дисперсии) зависимой переменной, объясненной независимой переменной. Учитывая, что он является описательным показателем, он не является статистическим критерием.
Чтобы выяснить, может ли наша регрессионная модель быть статистически значимой, нам нужно построить F-статистику.
В целом, мы используем F-распределенную статистику для сравнения двух вариаций (дисперсий).
В регрессионном анализе мы можем использовать F-распределенную статистику, чтобы проверить (нулевую) гипотезу о том, равны ли коэффициенты наклона регрессии нулю. Эти наклоны обозначаются как \(b_i\).
Альтернативная гипотеза заключается в том, что, по крайней мере, один наклон не равен нулю:
\( H_0 \): \( b_1 = b_2 = b_3 = \ \ldots \ = b_k = 0 \).
\( H_a \): По крайней мере один наклон \(b_k\) не равен нулю.
Для простой линейной регрессии эти гипотезы упрощаются до вида:
\( H_0 \): \( b_1 = 0 \).
\( H_a \): \( b_1 \neq 0 \).
F-распределенная статистика строится с использованием суммы квадратов регрессии и суммы квадратов ошибки, каждая из которых корректируется с учетом степеней свободы. Другими словами, это отношение двух дисперсий.
Мы делим сумму квадратов регрессии на количество независимых переменных, представленных \(k\). В случае простой линейной регрессии \(k = 1\), поэтому мы получаем среднеквадратическую регрессию (MSR, mean square regression), которая совпадает с суммой квадратов регрессии:
\( \begin{aligned}
{\rm MSR} &= \dst { \text{Сумма квадратов регрессии} \over k} \\[1ex]
&= \dst { \dst \sum^n_{i=1} (\hat Y_i - \overline Y)^2 \over 1 }
\end{aligned} \)
Итак, для простой линейной регрессии,
\( \dst \Large {\rm MSR} = \sum^n_{i=1} (\hat Y_i - \overline Y)^2 \) (11)
Затем мы рассчитываем среднеквадратическую ошибку (MSE, mean square error), которая представляет собой сумму квадратов ошибки, деленную на степени свободы, которые составляют \( n - k - 1 \).
В простой линейной регрессии выражение \( n - k - 1 \) приводится к \( n - 2 \):
\( \begin{aligned} \Large
{\rm MSE} &= \dst { \text{Сумма квадратов ошибки} \over n-k-1} \\
&= \dst { \dst \sum^n_{i=1} ( Y_i - \hat Y_i)^2 \over n-2 }
\end{aligned} \) (12)
Следовательно, F-распределенная статистика (MSR/MSE) равна:
\(
F = \dst {
\large { \text{Сумма квадратов регрессии} \over k } \over
\large { \text{Сумма квадратов ошибки} \over n-k-1} } = {{\rm MSR} \over {\rm MSE}}
\)
\dst { \sum^n_{i=1} ( \hat Y_i - \overline Y )^2 \over 1 } \over
\dst { \sum^n_{i=1} ( Y_i - \hat Y_i)^2 \over n-2 }
} \), (13)
которая распределяется с \(1\) и \(n - 2\) степенями свободы в простой линейной регрессии.
F-статистика в регрессионном анализе односторонняя, с областью отклонения гипотезы с правой стороны, поскольку нас интересует, является ли вариация в объясненной переменной \(Y\) (числитель) больше, чем вариация в необъясненной переменной \(Y\) (знаменатель).
