CFA - Допущения простой линейной регрессии
Рассмотрим допущения, лежащие в основе модели простой линейной регрессии, а также как остатки и графики остатков регрессии указывают на нарушение этих допущений, - в рамках изучения количественных методов по программе CFA (Уровень II).
Мы обсудили, как интерпретировать коэффициенты в модели простой линейной регрессии. Теперь мы обращаемся к статистическим допущениям, лежащим в основе этой модели.
Предположим, что у нас есть \(n\) наблюдений как зависимой переменной \(Y\), так и независимой переменной \(X\), и мы хотим оценить простую линейную регрессию \(Y\) по \(X\).
Нам нужно сделать следующие четыре ключевых предположения (допущения), чтобы получить обоснованные выводы из простой линейной регрессии:
- Линейность (linearity): зависимость между зависимой переменной \(Y\) и независимой переменной \(X\) является линейной.
- Гомоскедастичность (homoskedasticity): дисперсия остатков (случайных ошибок) регрессии одинакова для всех наблюдений.
- Независимость (independence): парные наблюдения \(Y\) и \(X\) не зависят друг от друга. Это подразумевает, что остатки регрессии не коррелируют между наблюдениями.
- Нормальность (normality): остатки регрессии нормально распределены.
Теперь мы более подробно рассмотрим каждое из этих допущений и объясним «наилучшую практику» анализа графика остатков результатов регрессии, позволяющую выявить потенциальные нарушения этих ключевых допущений.
Допущение 1: Линейность.
Мы строим линейную модель, поэтому мы должны предположить, что истинная взаимосвязь или зависимость между зависимыми и независимыми переменными является линейной.
Если зависимость между независимыми и зависимыми переменными является нелинейной по параметрам, то оценка этой зависимости с помощью модели простой линейной регрессии даст неверные результаты: модель будет смещена (т.е. ошибочна), поскольку она будет недооценивать и переоценивать зависимую переменную в определенных точках.
Например, зависимость \(Y_i = b_0 e^{b_1 X_i} + \epsilon_i \) является нелинейной по \(b_1\), поэтому мы не должны применять к ней модель линейной регрессии.
В Иллюстрации 10 показан пример этой экспоненциальной модели с указанной линией регрессии.
Вы можете видеть, что эта линия плохо соответствует этой взаимосвязи: для более низких и более высоких значений \(X\) линейная модель недооценивает \(Y\), тогда как для средних значений линейная модель переоценивает \(X\).
Иллюстрация 10. Иллюстрация нелинейной связи, оцененной как линейная связь.
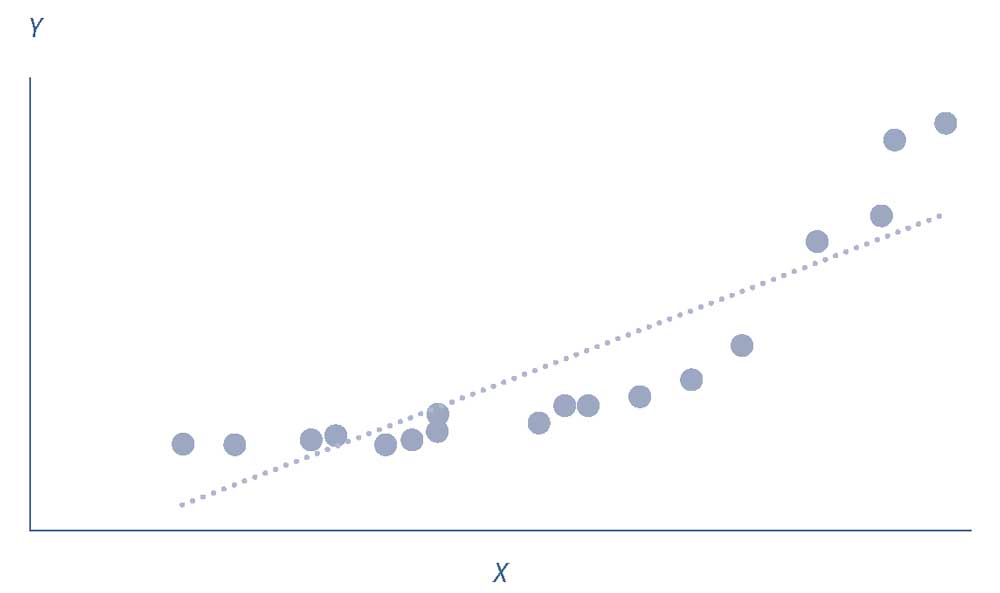
Иллюстрация нелинейной связи, оцененной как линейная связь.
Еще одно значение этого допущения заключается в том, что независимая переменная \(X\) не должна быть случайной; то есть она нестохастическая или неслучайная.
Если независимая переменная является случайной, это означает, что между зависимыми и независимыми переменными нет линейной связи.
Хотя мы можем первоначально предполагать, что независимая переменная в регрессионной модели не является случайной величиной, это допущение не всегда может быть истинным.
Когда мы рассматриваем остатки модели, мы ожидаем, что остатки являются случайными. Остатки не должны демонстрировать определенный шаблон (т.е. закономерность) при нанесении на график независимой переменной.
Как показано в Иллюстрации 11, остатки линейной регрессии из Иллюстрации 10, по-видимому, не являются случайными, а, скорее, демонстрируют связь с независимой переменной \(X\), опускающуюся ниже некоторого диапазона \(X\) и поднимающуюся выше другого диапазона.
Иллюстрация 11. Иллюстрация остатков в нелинейной связи, оцененной как линейная связь.
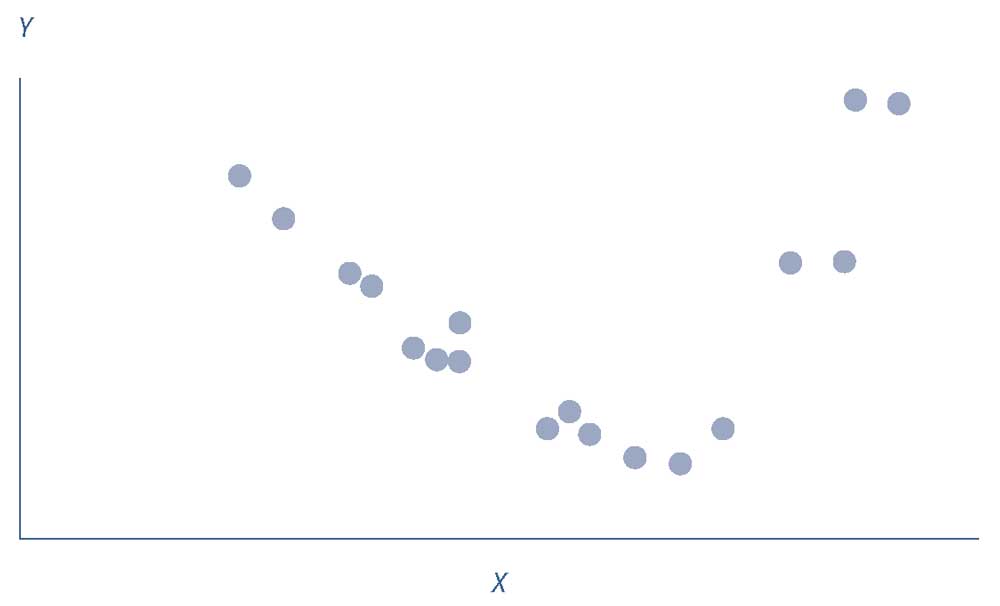
Иллюстрация остатков в нелинейной связи, оцененной как линейная связь.
Допущение 2: Гомоскедастичность.
Предположение о том, что дисперсия остатков одинакова для всех наблюдений, известно как допущение о гомоскедастичности.
Математически, это допущение выражается в квадратных остатках:
\( \Large E \big( \epsilon^2_i \big) = \sigma^2_{\epsilon} , \ i = 1, \ldots , n \) (8)
Если остатки не являются гомоскедастическими, то есть, если дисперсия остатков неодинакова для наблюдений, то мы называем это гетероскедастичностью (heteroskedasticity).
Предположим, вы изучаете временные ряды краткосрочных процентных ставок в качестве зависимой переменной и показатели инфляции в качестве независимой переменной за промежуток в 16 лет.
Мы можем полагать, что краткосрочные процентные ставки \((Y)\) и показатели инфляции \((X)\) должны быть связаны (то есть процентные ставки растут при более высоком уровне инфляции).
Если рассматриваемый временной горизонт охватывает много лет, и в последние 8 лет центральный банк предпринимал определенные меры, которые искусственно снижали краткосрочные процентные ставки, то, вероятно, остатки в этой предполагаемой модели будут соответствовать двум разным моделям.
Мы будем называть первые 8 лет Режимом 1 (нормальные ставки) и вторые 8 лет Режимом 2 (низкие ставки). Если модель по-разному вписывается в эти два режима, то остатки и их дисперсии будут разными.
Вы можете увидеть эту ситуацию в Иллюстрации 12, которая показывает точечный график с построенной линией регрессии.
Коэффициент наклона линии регрессии в течение всех 16 лет составляет 1.1979.
Иллюстрация 12. Точечный график процентных ставок \((Y)\) и показателей инфляции \((X)\).
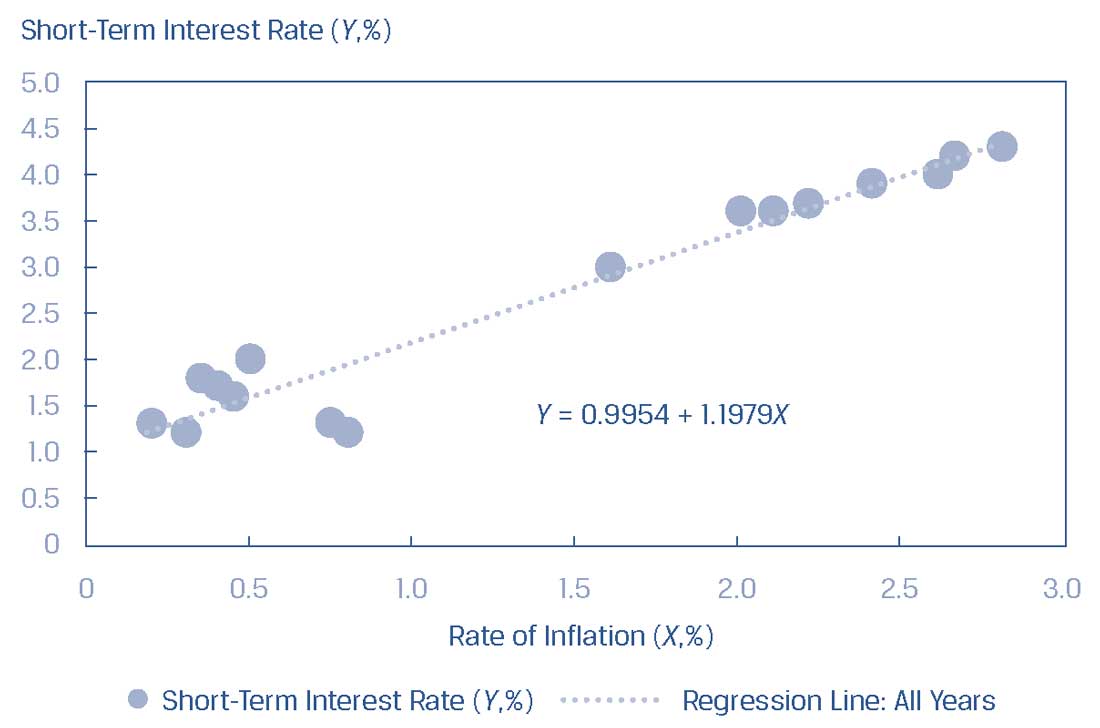
Точечный график процентных ставок \((Y)\) и показателей инфляции \((X)\).
На этом графике мы показываем остатки этой модели из Иллюстрации 13.
На графике указано расстояние двух стандартных отклонений от нуля (среднее значение остатков) в течение первых восьми лет, а затем в течение вторых восьми лет.
Как вы можете видеть, остатки выглядят разными для двух режимов: дисперсия (вариация) остатков в течение первых восьми лет намного меньше, чем дисперсия за вторые восьми лет.
Иллюстрация 13. График остатков регрессии для процентных ставок \((Y)\) и показателей инфляции \((X)\).
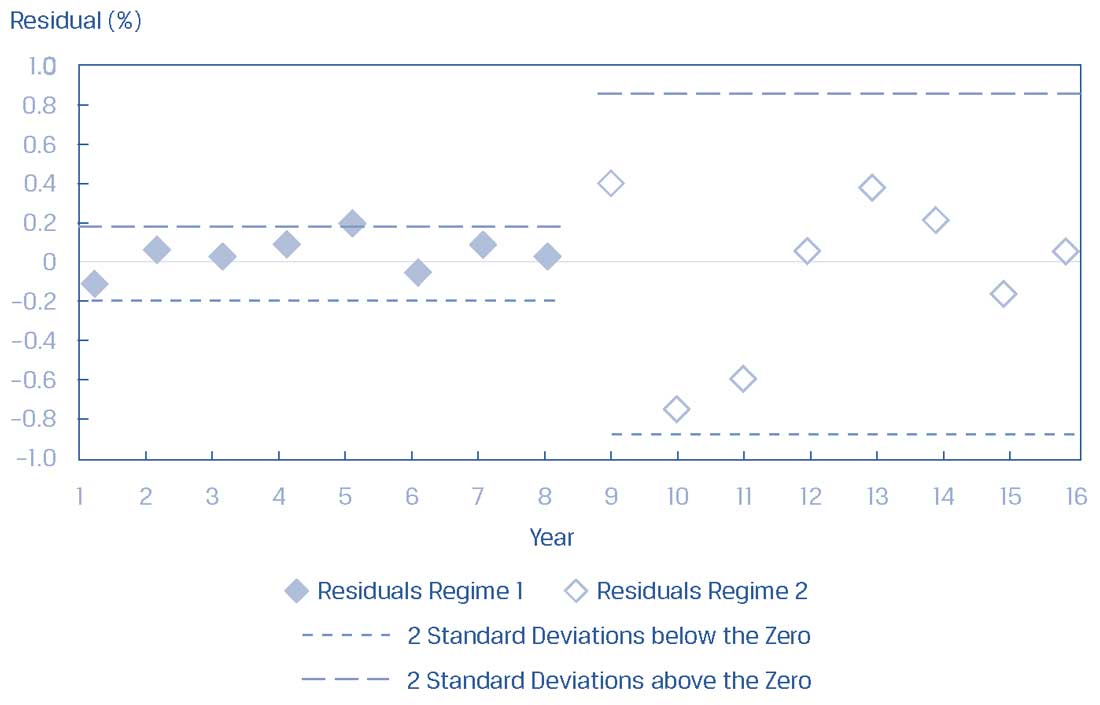
График остатков регрессии для процентных ставок \((Y)\) и показателей инфляции \((X)\).
Почему это происходит?
Модель кажется подходящей, но когда мы исследуем остатки (Иллюстрация 13), мы видим, что модель лучше подходит в течение одного периода по сравнению с другим периодом.
Такой анализ остатков на графике является важным этапом оценки соответствия модели.
Разница в дисперсии остатков между двумя режимами очевидна благодаря гораздо более широкой полосе разброса остатков для режима 2 (период низких ставок). Это указывает на явное нарушение допущения о гомоскедастичности.
Если мы изучим линию регрессии для каждого режима, мы увидим, что модели для двух режимов совершенно различны, что показано в Иллюстрации 14.
Для Режима 1 (нормальные ставки) наклон составляет 1.0247, тогда как для Режима 2 (низкие ставки) наклон составляет -0.2805.
В целом, кластеризация остатков в двух группах с совершенно разными дисперсиями ясно указывает на существование различных режимов зависимости между краткосрочными процентными ставками и показателями инфляции.
Иллюстрация 14. Линии регрессии для двух режимов.
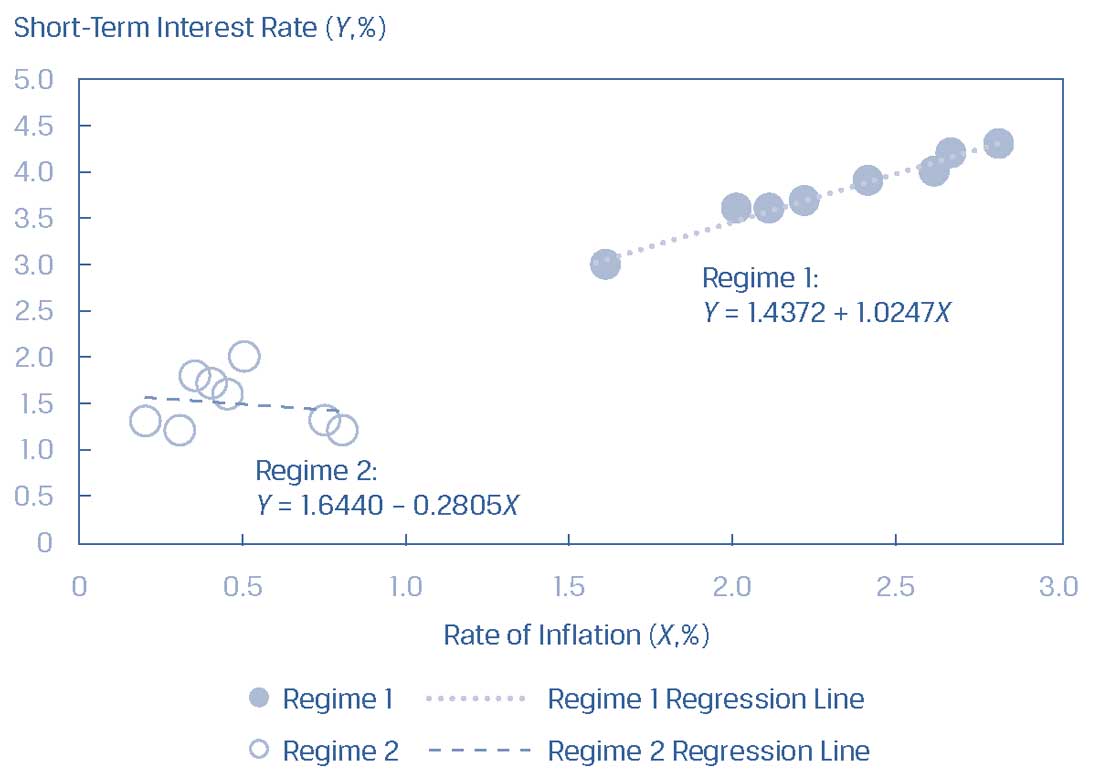
Линии регрессии для двух режимов.
Допущение 3: Независимость.
Мы допускаем, что парные наблюдения \(Y\) и \(X\) не коррелируют друг с другом, что означает, что они независимы.
Если существует корреляция между наблюдениями (то есть автокорреляция), они не являются независимыми, и остатки будут коррелировать.
Допущение о том, что остатки не коррелируют между наблюдениями, также необходимо для правильной оценки дисперсий оценочных параметров \(b_0\) и \(b_1\) (то есть \(\hat b_0\) и \(\hat b_1\)), которые мы используем в проверке гипотез о точке пересечения и наклоне соответственно.
Важно выяснить, демонстрируют ли остатки шаблон, что означает нарушение этого допущения. Поэтому нам необходимо визуально и статистически исследовать остатки для регрессионной модели.
Рассмотрим ежеквартальную выручку компании, регрессирующую в течение более 40 кварталов, как показано в Иллюстрации 15. На графике также построена линия регрессии.
Понятно, что эта выручка отображает сезонный шаблон, что свидетельствует об автокорреляции.
Иллюстрация 15. Регрессия квартальной выручки по 40 квартальным периодам.
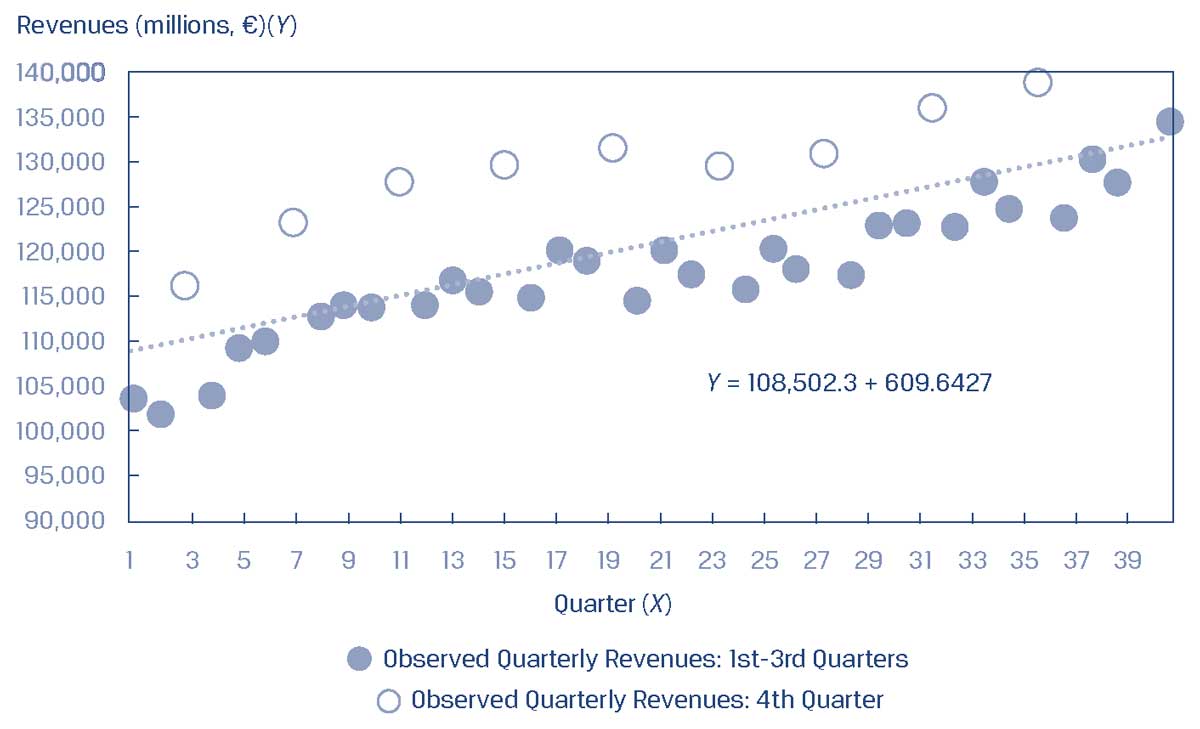
Регрессия квартальной выручки по 40 квартальным периодам.
В Иллюстрации 16 мы строим на графике остатки из этой модели и видим, что в них есть шаблон. Эти остатки коррелируют, в частности, резко повышаются в 4-м квартале, а затем откатываются в последующий квартал.
В целом, шаблоны (закономерности) в обеих Иллюстрациях 15 и 16 указывают на нарушение допущения о независимости.
Иллюстрация 16. График остатков для квартальной выручки.
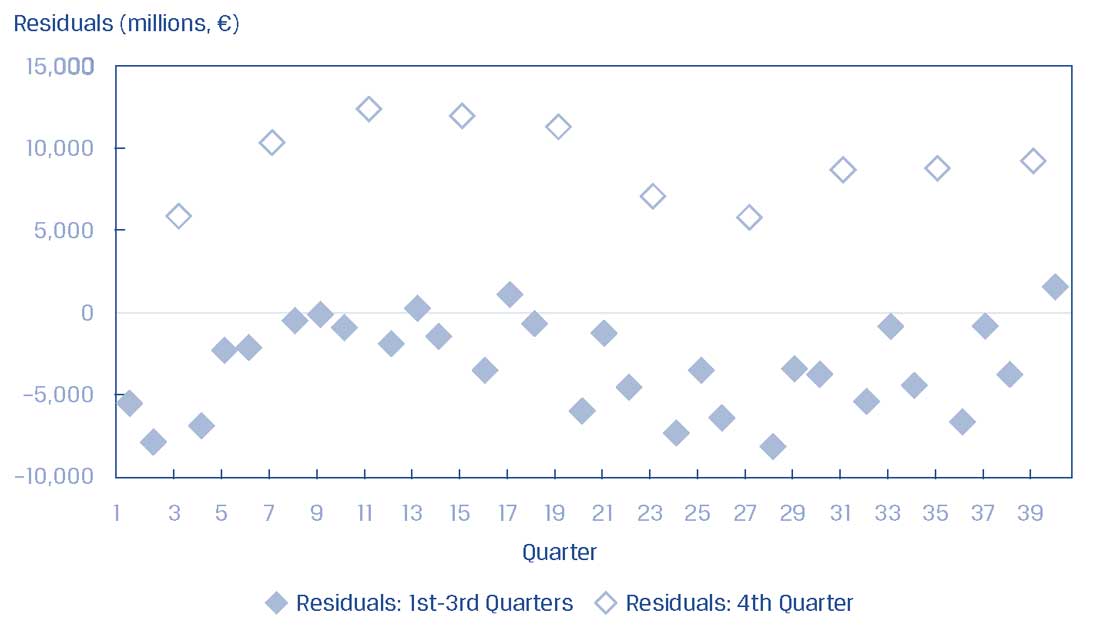
График остатков для квартальной выручки.
Допущение 4: Нормальность.
Допущение о нормальности требует, чтобы остатки были нормально распределены.
Это не означает, что зависимые и независимые переменные должны быть нормально распределены; это только означает, что остатки модели нормально распределены.
Тем не менее, при оценке любой модели хорошей практикой является анализ распределения зависимых и независимых переменных для изучения выбросов.
Выброс в одной или обеих переменных может существенно изменить построение линии регрессии таким образом, что модель будет плохо соответствовать большинству других наблюдений.
При нормально распределенных остатках мы можем проверить конкретную гипотезу о модели линейной регрессии.
При больших размерах выборки мы можем отказаться от допущения о нормальности, обратившись к центральной предельной теореме.
Асимптотическая теория (которая занимается большими выборками) показывает, что во многих случаях статистические критерии, создаваемые стандартными программами регрессии, являются верными, даже если остатки модели не соответствуют нормальному распределению.
Пример 4. Допущения простой линейной регрессии.
Аналитик исследует доходы компании и оценивает простую линейную модель временных рядов, регрессируя выручку по временным периодам, которые измеряются в годах - \(1, 2 , \ \ldots \ , 15\).
Она представляет на графике наблюдаемую выручку компании и линию регрессии, как показано в Иллюстрации 17. Она также представляет на графике остатки этой регрессионной модели, как показано в Иллюстрации 18.
Иллюстрация 17. Сравнение выручки за периоды с использованием простой линейной регрессии.
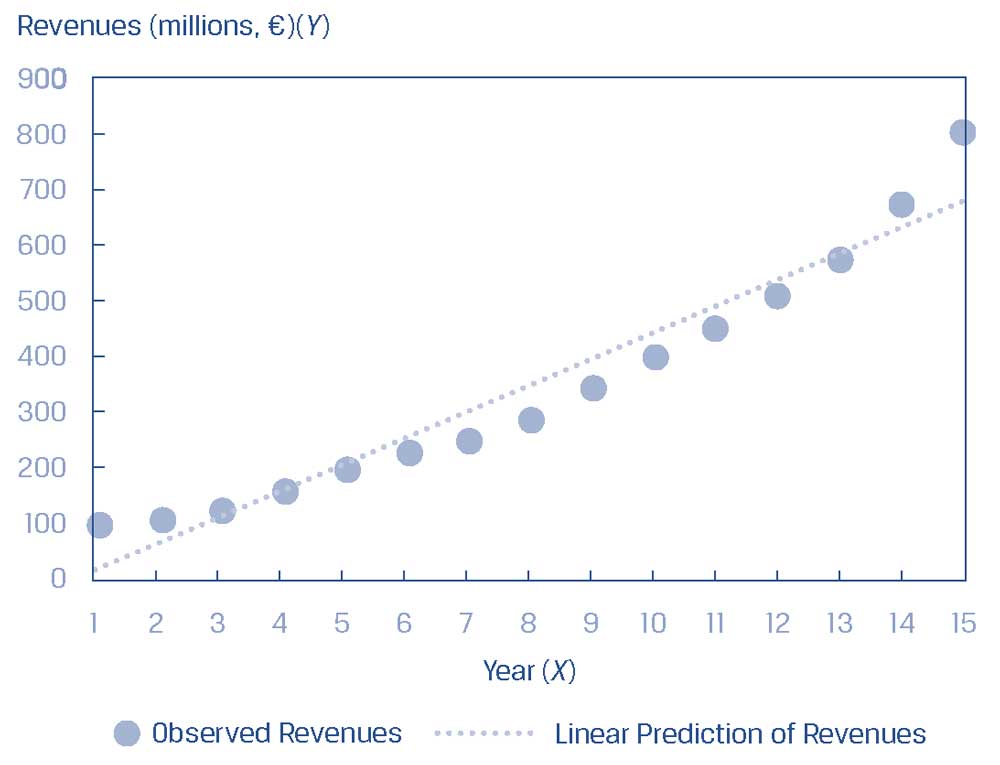
Сравнение выручки за периоды с использованием простой линейной регрессии.
Иллюстрация 18. График остатков для выручки за годовые периоды.
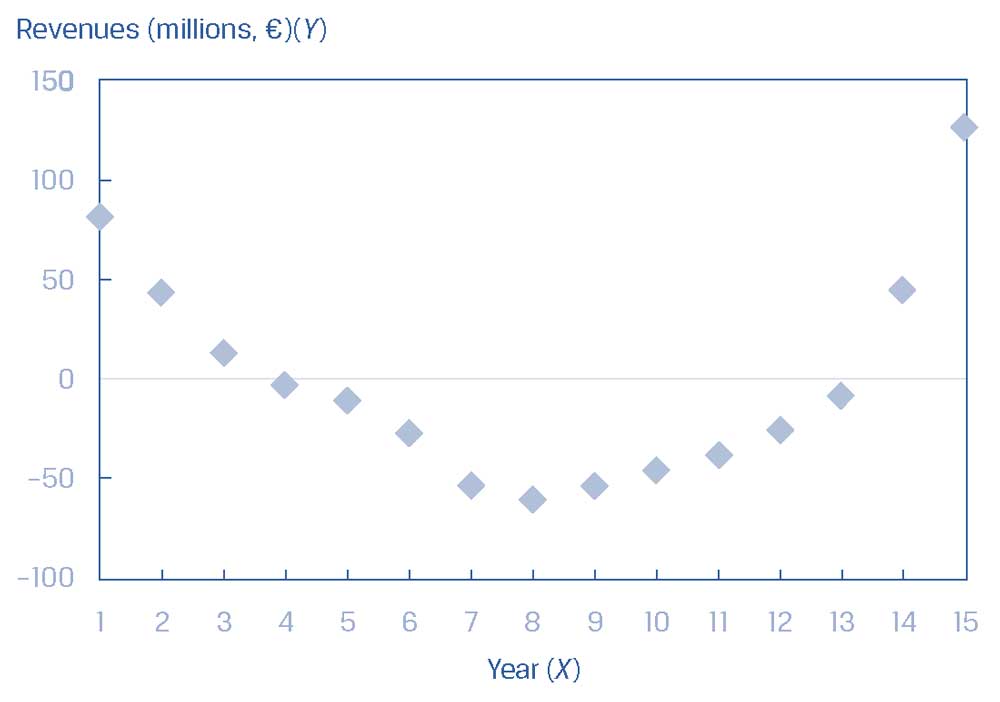
График остатков для выручки за годовые периоды.
Основываясь на иллюстрациях 17 и 18, опишите, какие допущения о простой линейной регрессии может нарушать модель аналитика.
Решение.
Правильная модель не является линейной, как видно из шаблона выручки в Иллюстрации 17.
В ранние годы (т.е. 1 и 2) и более поздние годы (т.е. 14 и 15) линейная модель недооценивает выручку, тогда как в средние годы (т.е. 7-11) линейная модель переоценивает выручку.
Более того, изогнутый шаблон остатков в Иллюстрации 18 указывает на потенциальную гетероскедастичность (остатки имеют неравные дисперсии), отсутствие независимости наблюдений и ненормальность (что является проблемой, учитывая небольшой размер выборки \(n = 15\)).
В целом, аналитик должен быть обеспокоен тем, что модель нарушает все допущения, регулирующие простую линейную регрессию (линейность, гомоскедастичность, независимость и нормальность).
