CFA - Выбор правильной функциональной формы регрессии
Рассмотрим особенности выбора подходящей функциональной формы простой линейной регрессии, - в рамках изучения количественных методов по программе CFA (Уровень II).
Ключом к подбору подходящей функциональной формы простой линейной регрессии является изучение степени согласия показателей - коэффициента детерминации (\(R^2\)), F-статистики и стандартной ошибки оценки (\(s_e\)), а также изучение того, есть ли закономерности в остатках регрессии.
В дополнение к подбору критериев, большинство статистических пакетов строят графики остатков как часть результатов расчета регрессии, что позволяет визуально изучить остатки. В этих графиках важно проанализировать случайность остатков.
В качестве примера рассмотрим взаимосвязь между ежемесячной доходностью акций DEF и ежемесячной доходностью индекса акций EAA, как показано в Панели A Иллюстрации 39, где приведена соответствующая линия регрессии.
Используя уравнение для этой линии регрессии, мы рассчитываем остатки и отражаем их на графике для индекса акций EAA, как показано в Панели B Иллюстрации 39. Остатки, по-видимому, являются случайными, и не несут в себе связь с независимой переменной.
Распределение остатков, показанное в Панели C Иллюстрации 39, показывает, что остатки приблизительно нормально распределены.
Используя статистическое ПО, мы можем продолжить исследование, изучив распределение остатков, включая использование графика нормального распределения вероятности или критериев для проверки нормальности остатков.
Иллюстрация 39. Ежемесячная доходность акций DEF регрессирует по доходности индекса EAA.
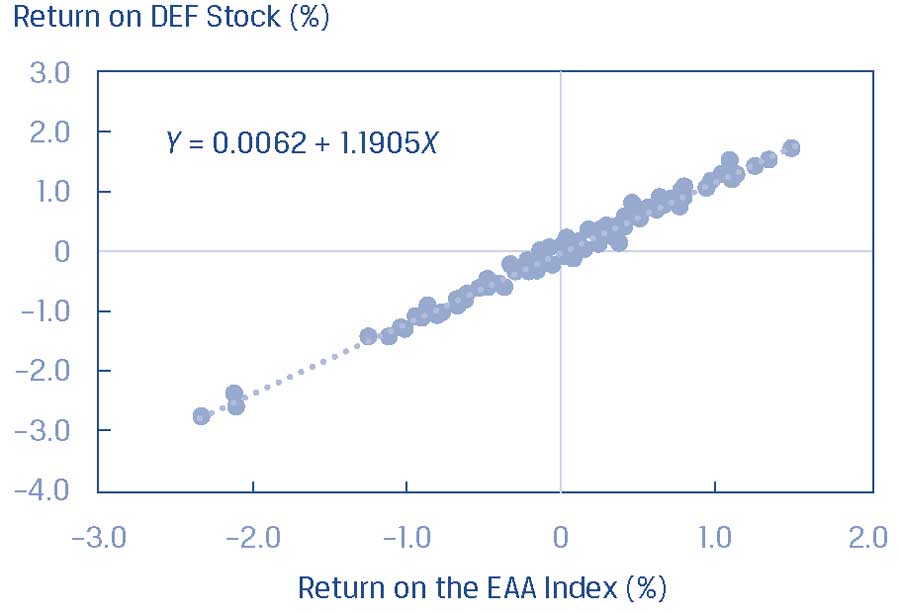
Панель A. График рассеяния доходности акций DEF и доходности индекса EAA.
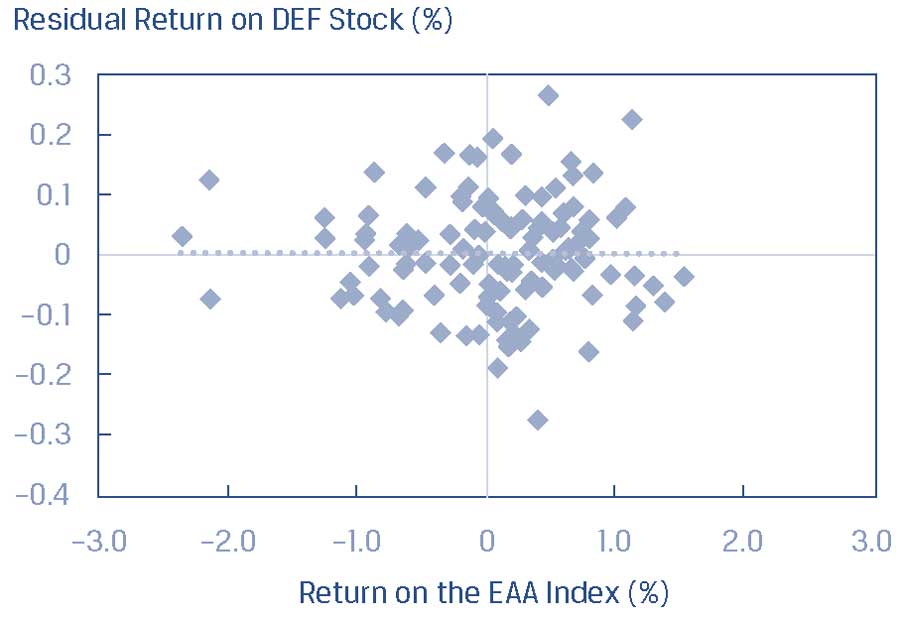
Панель B. График рассеяния остатков и доходности индекса EAA.
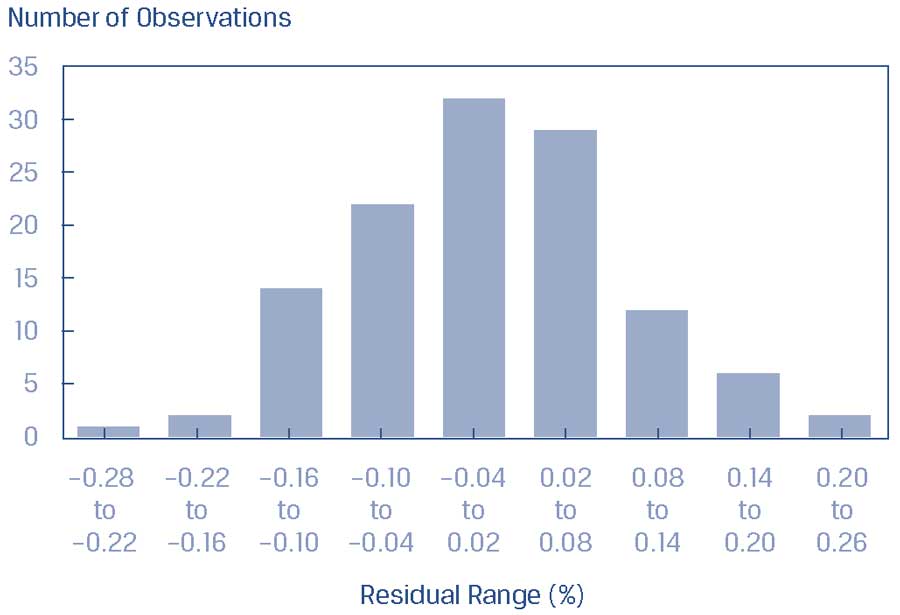
Панель C. Гистограмма остатков.
Пример 8. Сравнение функциональных форм.
Аналитик исследует взаимосвязь между годовым ростом потребительских расходов (CONS) в стране и годовым ростом ВВП страны (GGDP).
Аналитик оценивает следующие две модели:
|
Модель 1 |
Модель 2 |
|
|---|---|---|
|
\( {\rm GGDP}_i = b_0 + b_1 {\rm CONS}_i + \epsilon_i \) |
\( {\rm GGDP}_i = b_0 + b_1 \ln {\rm CONS}_i + \epsilon_i \) |
|
|
Точка пересечения (константа) |
1.040 |
1.006 |
|
Наклон |
0.669 |
1.994 |
|
\(R^2\) |
0.788 |
0.867 |
|
Стандартная ошибка оценки |
0.404 |
0.320 |
|
F-статистика |
141.558 |
247.040 |
- Определите функциональную форму, используемую в этих моделях.
- Объясните, какая модель имеет лучшую степень согласия с данными выборки.
Решение.
- Модель 1 - это простая линейная регрессия без преобразования переменной, тогда как Модель 2 - это модель lin-log с натуральным логарифмом переменной CONS в качестве независимой переменной.
- Модель 2 - это модель lin-log, которая лучше подходит данным.
Поскольку зависимая переменная одинакова для двух моделей, мы можем сравнить соответствие моделей, используя либо относительные показатели (\(R^2\) или F-статистику), либо абсолютную меру соответствия, стандартную ошибку оценки.
Стандартная ошибка оценки ниже для Модели 2, тогда как \(R^2\) и F-статистика выше для модели 2 по сравнению с Моделью 1.
