fin-accounting

воскресенье, 4 февраля 2024

CFA - Расчет параметров простой линейной регрессии

Рассмотрим основы расчета простой линейной регрессии, построение линии регрессии, а также практический пример регрессионного анализа рентабельности активов (ROA) по капитальным затратам (CAPEX), - в рамках изучения количественных методов по программе CFA (Уровень II).

Основы простой линейной регрессии.

Регрессионный анализ начинается с определения зависимой переменной (dependent variable) - т.е., переменной, чью вариацию (изменение) вы хотите объяснить.

Независимая переменная (independent variable) - это переменная, чья изменение вы используете для объяснения вариации (изменений) зависимой переменной.

Например, вы можете попытаться объяснить доходность акций (зависимая переменная), используя ставки доходности индекса S&P 500 (независимая переменная).

Или вы можете попытаться объяснить уровень инфляции в стране (зависимая переменная) как функцию роста денежной массы (независимая переменная).

Как следует из названия, линейная регрессия (linear regression) предполагает линейную связь между зависимыми и независимыми переменными.

Цель состоит в том, чтобы построить линию на точечном графике между парными наблюдениями переменных \(Y\) и \(X\) так, чтобы минимизировать квадратные отклонения от этой линии.

Это называется критерием наименьших квадратов или критерием по методу наименьших квадратов (least squares criterion) - поэтому такую регрессию также называют регрессией наименьших квадратов (least squares regression).

Из-за широкого практического применения линейную регрессию часто называют обычной регрессией наименьших квадратов (OLS, ordinary least squares).

Линейное соотношение между зависимыми и независимыми переменными описывается следующей формулой:

\( \dstl Y_i = b_0 + b_1 X_i + \epsilon_i, \ i=1, \ \ldots \ , n \) (3)

Уравнение 3 - это модель, которая не требует, чтобы каждая пара значений \((Y, X))\ для наблюдения падала на линию регрессии.

Это уравнение гласит, что зависимая переменная \(Y\) равна точке пересечения \(b_0\) плюс коэффициент наклона \(b_1\), умноженный на независимую переменную \(X\), плюс случайная ошибка \(\epsilon\).

Точка пересечения (intercept) \(b_0\), которую также называют константой, - это значение зависимой переменной \(Y\), при котором независимая переменная \(X\) равна нулю. То есть, это точка пересечения линии регрессии с осью \(Y\).

Случайная ошибка или просто ошибка (error term), представляет собой разницу между наблюдаемым значением \(Y\) и значением, ожидаемым в результате зависимости между \(Y\) и \(X\) в их общей истинной совокупности.

Мы называем точку пересечения \(b_0\) и коэффициент наклона \(b_1\) коэффициентами регрессии (англ. 'regression coefficients').

Мы часто описываем эту зависимость простой линейной регрессии:

как регрессию переменной \(Y\) и по переменной \(X\) или
как то, что \(Y\) регрессирует по \(X\).

Рассмотрим диаграмму рассеяния ROA и CAPEX из Иллюстрации 3, использовав ее в Иллюстрации 4 и добавив в нее линию регрессии.

Эта линия представляет среднюю взаимосвязь между ROA и CAPEX; не каждое наблюдение попадает на линию, но линия описывает взаимосвязь по среднему значению между ROA и CAPEX.

Иллюстрация 4. Линия регрессии для ROA и CAPEX.

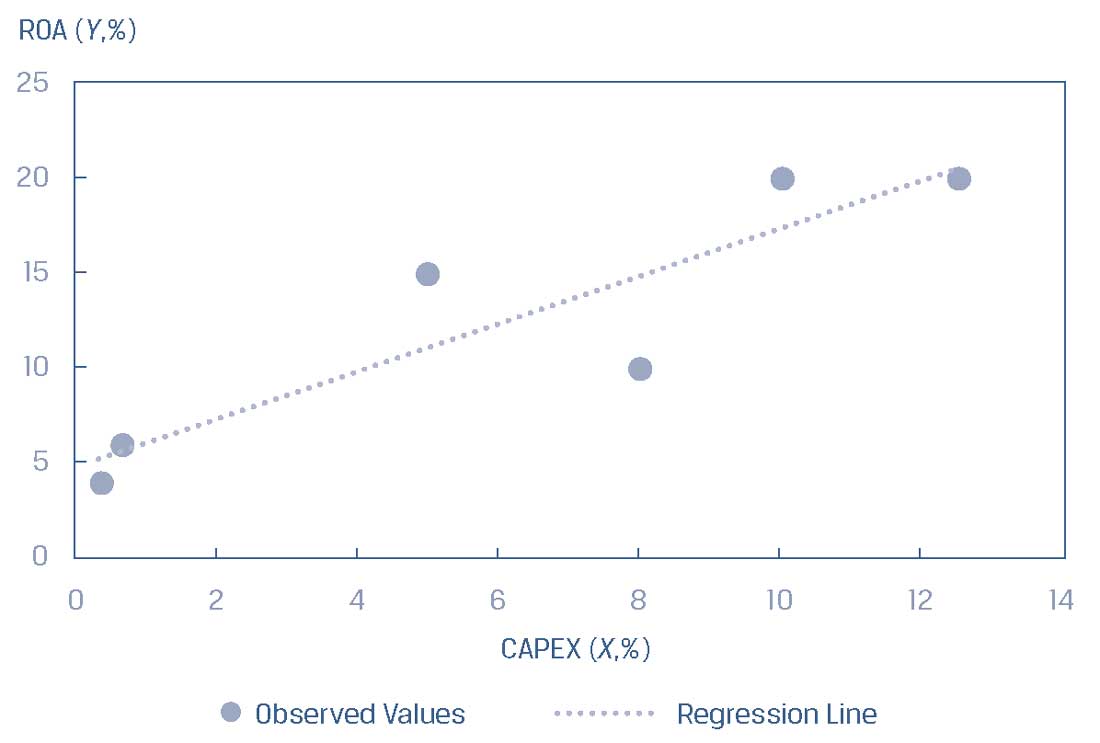
Линия регрессии для ROA и CAPEX.

Как рассчитать линию регрессии?

Мы не можем наблюдать за значениями параметров \(b_0\) и \(b_1\) в регрессионной модели.

Вместо этого мы наблюдаем только \(\hat b_0\) и \( \hat b_1\), которые являются оценками (на что указывают «шапки» над коэффициентами) параметров совокупности, основанными на выборке.

Таким образом, прогнозы должны основываться на оценочных значениях параметров, а проверка прогнозов основана на оценочных значениях в отношении гипотетических значений совокупности.

Мы оцениваем линию регрессии как линию, которая наилучшим образом соответствует наблюдениям.

В простой линейной регрессии оценочная константа \(\hat b_0\) и оценочный коэффициент наклона \(\hat b_1\) таковы, что сумма квадратных вертикальных расстояний от наблюдений до установленной линии регрессии сводится к минимуму.

Основное внимание здесь уделяется сумме квадратов разниц между наблюдениями переменной \(Y_i\) и соответствующим оценочным значением \(\hat Y_i\) на линии регрессии.

Мы представляем значение зависимой переменной для \(i\)-го наблюдения, которое падает на линию регрессии как \(\hat Y_i\), которое равно \(\hat b_0 + \hat b_1 X_i\).

\(\hat Y_i\) - это то, каким будет оценочное значение переменной \(Y\) для \(i\)-го наблюдения, основанного на средней взаимосвязи между \(Y\) и \(X\).

Отклонение или остаток (residual) для \(i\)-го наблюдения \(e_i\), показывает, насколько наблюдаемое значение \(Y_i\) отличается от значения \(\hat Y_i\), оцененного с использованием линии регрессии: \( e_i = Y_i - \hat Y_i \).

Обратите внимание на тонкую разницу между терминами ошибка и остаток:

Oшибка \(\epsilon\) относится к отклонению от истинной зависимости всей совокупности, тогда как остаток относится к отклонению от линейной зависимости, установленной на основе выборки из совокупности.

Расчет линии регрессии требует минимизации суммы квадратов ошибок (SSE, sum of squares error), также известной как остаточная сумма квадратов или остаточная дисперсия (residual sum of squares):

\( \begin{aligned} \dstl
{\rm SSE} &= \sum^{n}_{i=1} (Y_i - \hat Y_i) ^2 \\[1ex]
&= \sum^{n}_{i=1}
\left [Y_i - \Big(\hat b_0 + \hat b_1 X_i \Big) \right]^2 \\[1ex]
&= \sum^{n}_{i=1} e^2_i
\end{aligned} \) (4)

Используя регрессию наименьших квадратов для оценки значений параметров совокупности \(b_0\) и \(b_1\), мы можем провести линию через наблюдения \(X\) и \(Y\), которая объясняет значение, которое \(Y\) принимает для любого конкретного значения \(X\).

Как видно из Иллюстрации 5, отклонения (остатки) представлены вертикальными расстояниями от установленной линии регрессии (см. третье и пятое наблюдения для компаний C и E соответственно) и, следовательно, они выражены в единицах измерения зависимой переменной.

Остаток выражен в той же единице измерения, что и зависимая переменная: если зависимая переменная выражена в евро, то ошибка также выражена в евро, а если зависимая переменная является темпом роста, то и ошибка выражена как темп роста.

Иллюстрация 5. Отклонения (остатки) линейной регрессии.

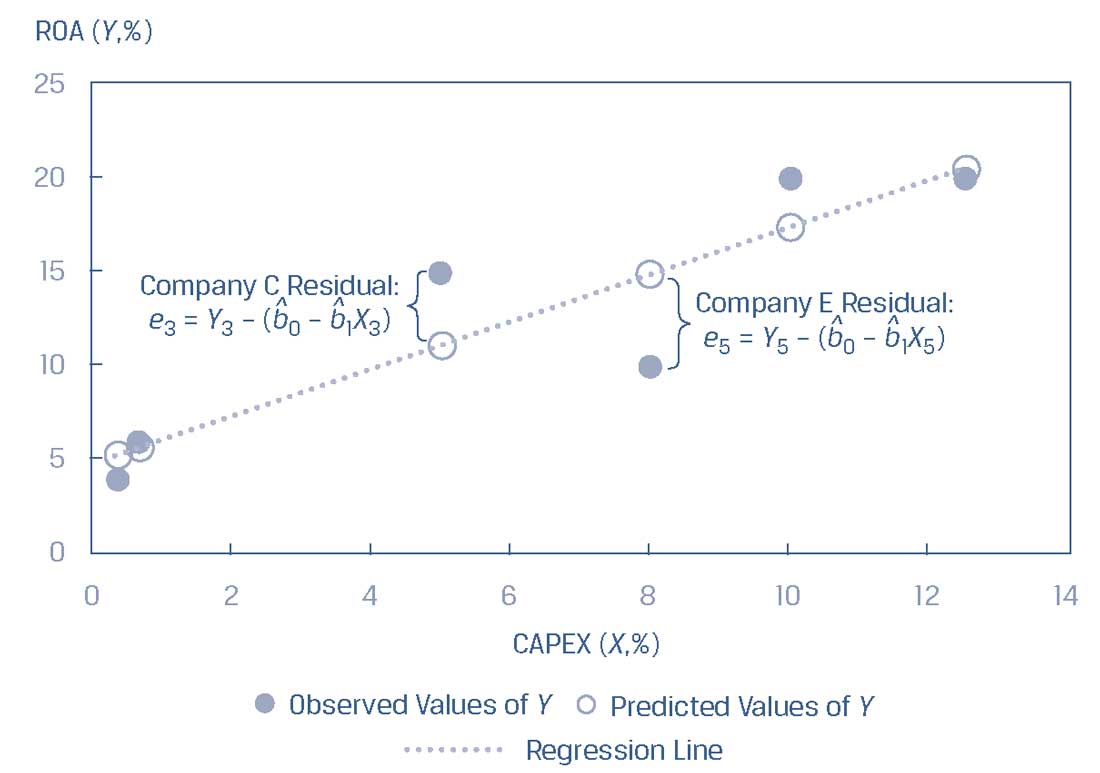
Отклонения (остатки) линейной регрессии

Как рассчитать константу \(\hat b_0\) и наклон \(\hat b_0\) для данной выборки парных наблюдений \( (Y, X) \)?

Наклон - это отношение ковариации между \(Y\) и \(X\) к дисперсии \(X\), где \(\overline Y\) - среднее значение переменной \(Y\) , а \(\overline X\) - среднее значение переменной \(X\):

\( \begin{aligned} \dst
\hat b_1 &= { \text{Ковариация } Y \text{ и } X \over
\text{Дисперсия } X} \\[1ex]
&= { \dst
{ \dst \sum^{n}_{i=1} (Y_i - \overline Y)(X_i - \overline X)
\over n-1}
\over
{ \dst \sum^{n}_{i=1} (X_i - \overline X)^2 \over n-1} }
\end{aligned} \)

Упростим до формулы:

\( \dstl
\hat b_1 = { \dst \sum^{n}_{i=1} (Y_i - \overline Y)(X_i - \overline X)
\over \dst \sum^{n}_{i=1} (X_i - \overline X)^2 }
\) (5)

Теперь, когда мы рассчитали наклон, мы можем определить константу (точку пересечения), используя среднее значение \(Y\) и среднее значение \(X\):

\( \dstl \hat b_0 = \overline Y - \hat b_1 \overline X \) (6)

Мы показываем расчет наклона и константы в Иллюстрации 6.

Иллюстрация 6. Расчет наклона и константы для модели регрессии ROA.

Компания	ROA \( (Y_i) \)	CAPEX \( (X_i) \)	\( (Y_i - \overline Y)^2 \)	\( (X_i - \overline X)^2 \)	\( (Y_i - \overline Y)(X_i - \overline X) \)
A	6.0	0.7	42.25	29.16	35.10
B	4.0	0.4	72.25	32.49	48.45
C	15.0	5.0	6.25	1.21	-2.75
D	20.0	10.0	56.25	15.21	29.25
E	10.0	8.0	6.25	3.61	-4.75
F	20.0	12.5	56.25	40.96	48.00
Сумма	75.0	36.6	239.50	122.64	153.30
Среднее арифметическое	12.5	6.100

Коэффициент наклона: \( \dst \hat b_1 = {153.30 \over 122.64} = 1.25 \)

Константа: \( \dst \hat b_0 = 12.5 - (1.25 \times 6.10) = 4.875 \)

Модель регрессии ROA: \( \dst \hat Y_i = 4.875 + 1.25 X_i + \epsilon_i \)

Обратите внимание на сходство формулы коэффициента наклона и формулы попарной корреляции. Корреляция выборки \(r\) - это коэффициент ковариации к произведению стандартных отклонений:

\( \dst
r = { \text{Ковариация } Y \text{ и } X \over
\Big( \text{Стандартное отклонение } Y \Big)
\Big( \text{Стандартное отклонение } X \Big)
} \)

Тонкая разница между формулами наклона и корреляции находится в знаменателе:

Для наклона это дисперсия независимой переменной, но для корреляции знаменатель является произведением стандартных отклонений.

Для нашего анализа ROA и CAPEX:

Ковариация \(Y\) и \(X\):

\( \dst
{\rm cov}_{XY} =
{ \dst \sum^{n}_{i=1} (Y_i - \overline Y)(X_i - \overline X)
\over n-1} = {153.30 \over 5} = 30.66
\) (7a)

Стандартное отклонение Y и X:

\( \dst
S_Y =
\sqrt{ \dst \sum^{n}_{i=1} (Y_i - \overline Y)^2
\over n-1} = \sqrt{239.50 \over 5} = 6.9210
\) (7b)

\( \dst
S_X =
\sqrt{ \dst \sum^{n}_{i=1} (X_i - \overline X)^2
\over n-1} = \sqrt{122.64 \over 5} = 4.9526
\)

\( \dst r = { 30.66 \over (6.9210) (4.9526) } 0.89458945 \).

Поскольку знаменатели, как наклона, так и корреляции являются положительными, знаки наклона и корреляции управляются числителем:

Если ковариация является положительной, то как наклон, так и корреляция являются положительными, а если ковариация отрицательная, то как наклон, так и корреляция отрицательны.

Как аналитики рассчитывают простую линейную регрессию?

Как правило, аналитик будет использовать функции анализа данных в электронных таблицах, таких как Microsoft Excel, или статистический пакет на языках программирования R или Python для проведения линейного регрессионного анализа.

Ниже приведены некоторые из наиболее распространенных вариантов, которые используются на практике.