CFA - Прогнозирование с использованием простой линейной регрессии
Рассмотрим прогнозирование значения зависимой переменной в простой линейной регрессии, а также создание интервалов прогнозирования, - в рамках изучения количественных методов по программе CFA (Уровень II).
Финансовым аналитикам часто приходится использовать результаты регрессии, чтобы делать прогнозы о зависимой переменной.
Например, мы можем задаться вопросом: «Как быстро будут расти продажи корпорации XYZ в этом году, если реальный ВВП вырастет на 4%?»
Но мы не просто заинтересованы в получении таких прогнозов; мы также хотим знать, насколько мы можем быть уверены в результатах прогнозов.
Прогнозируемое значение зависимой переменной \( \hat Y_f \) определяется с использованием оценочных значений точки пересечения (константы) и наклона, а также ожидаемого или прогнозируемого значения независимой переменной \( X_f \):
\( \dstl \hat Y_f = \hat b_0 + \hat b_1 X_f \) (18)
В нашей модели регрессии ROA (рентабельность активов) если мы прогнозируем, что CAPEX компании составляет 6%, то прогнозируемая ROA в соответствии с Формулой 18 составит 12.375%:
\( \dst \hat Y_f = 4.815 + (1.25 \times 6) = 12.375 \)
Тем не менее, мы должны учитывать, что оценочная линия регрессии не описывает взаимосвязь между зависимыми и независимыми переменными; это среднее значение взаимосвязи между двумя переменными. Это очевидно, потому что не все остатки равны нулю.
Следовательно, для отражения этой неопределенности необходима интервальная оценка прогноза. Расчетная дисперсия ошибки прогнозирования \( s^2_f \) переменной \(Y\) при независимой переменной \(X\) равна:
\( \begin{aligned}
s^2_f &= \dst s^2_e
\left[ 1 + \dst {1 \over n} + \dst {(X_f - \overline X)^2 \over (n-1) s^2_X} \right] \\
&= \dst s^2_e
\left[ 1 + \dst {1 \over n} + \dst {(X_f - \overline X)^2 \over
\sum^n_{i=1} (X_i - \overline X)^2 }
\right] \end{aligned} \),
а стандартная ошибка прогноза:
\( \dstl s_f = s_e \dst \sqrt {
1 + \dst {1 \over n} + \dst { (X_f - \overline X)^2 \over
\sum^n_{i=1} (X_i - \overline X)^2 }
} \) (19)
Стандартная ошибка прогноза зависит от:
- стандартной ошибки оценки \(s_e\);
- количества наблюдений \(n\);
- прогнозируемого значения независимой переменной \(X_f\), используемого для прогнозирования зависимой переменной и ее отклонения от оценочного среднего \( \overline X \); а также
- изменения независимой переменной.
Из формулы для стандартной ошибки прогноза мы можем увидеть следующее:
- Чем лучше подбор модели регрессии, тем меньше стандартная ошибка оценки (\(s_e\)) и, следовательно, тем меньше стандартная ошибка прогноза.
- Чем больше размер выборки (\(n\)) в расчете регрессии, тем меньше стандартная ошибка прогноза.
- Чем ближе прогнозируемая независимая переменная (\(X_f\)) к среднему значению независимой переменной (\( \overline X \)), используемой в расчете регрессии, тем меньше стандартная ошибка прогноза.
Когда мы получим эту оценку стандартной ошибки прогноза, нам необходимо определить интервал прогнозирования зависимой переменной ( \(\hat Y_f\) ). Это очень похоже на оценку доверительного интервала параметра.
Интервал прогнозирования равен:
\( \dstl \hat Y_f \pm t_{ \text{ крит. для} \ \ \alpha / 2^S f } \) (20)
Мы описываем шаги для определения интервала прогнозирования в Иллюстрации 31.
Иллюстрация 31. Создание интервала прогнозирования зависимой переменной.
|
1 |
Прогнозируйте значение \( Y \), \( \hat Y_f \), учитывая прогнозируемое значение \( X \), \( X_f \). |
|
2 |
Выберите уровень значимости \( \alpha \) для интервала прогнозирования. |
|
3 |
Определите критическое значение для интервала прогнозирования, основанного на степени свободы и уровне значимости. |
|
4 |
Рассчитайте стандартную ошибку прогноза. |
|
5 |
Рассчитайте \( (1 - \alpha) \) процентный интервал прогнозирования: \( \hat Y_f \pm t_{ \text{ крит. для} \ \ \alpha / 2^S f } \). |
Учитывая, что прогнозируемое значение CAPEX составляет 6.0, прогнозируемое значение \( Y \) для нашей регрессионной модели ROA составляет 12.375:
\( \hat Y_f = 4.815 + 1.25 X_f = 4.875 + (1.25 \times 6.0) = 12.375 \).
Предполагая, что уровень значимости (\(\alpha\)) равен 5%, с \( n-2 \) степенями свободы (df = 4), критические значения для интервала прогнозирования составляют \( \pm 2.776 \).
Стандартная ошибка прогноза:
\( \begin{aligned} s_f &=
3.459588 \sqrt { 1+{1 \over 6} + \dst { (6-6.1)^2 \over 122.640 } } \\
&= 3.459588 \sqrt {1.166748} = 3.736912
\end{aligned} \).
Затем 95% интервал прогнозирования становится:
\( 12.375 \pm 2.776 (3.736912) \)
\( 12.375 \pm 10.3737 \)
\( \Bigl\{ 2.0013 < \hat Y_f < 22.7487 \Bigr\} \)
В нашем примере регрессии ROA мы можем увидеть, как изменяется стандартная ошибка прогноза (\(s_f\)), поскольку наше прогнозируемое значение независимой переменной становится дальше от среднего значения независимой переменной \( (X_f - \overline X) \) в Иллюстрации 32.
Среднее значение CAPEX равно 6.1%, и диапазон, который представляет одну стандартную ошибку прогноза, выше и ниже прогноза, сводится к минимуму в этой точке, и увеличивается, когда независимая переменная удаляется от \( \overline X \).
Иллюстрация 32. Прогнозы ROA и стандартная ошибка прогноза.
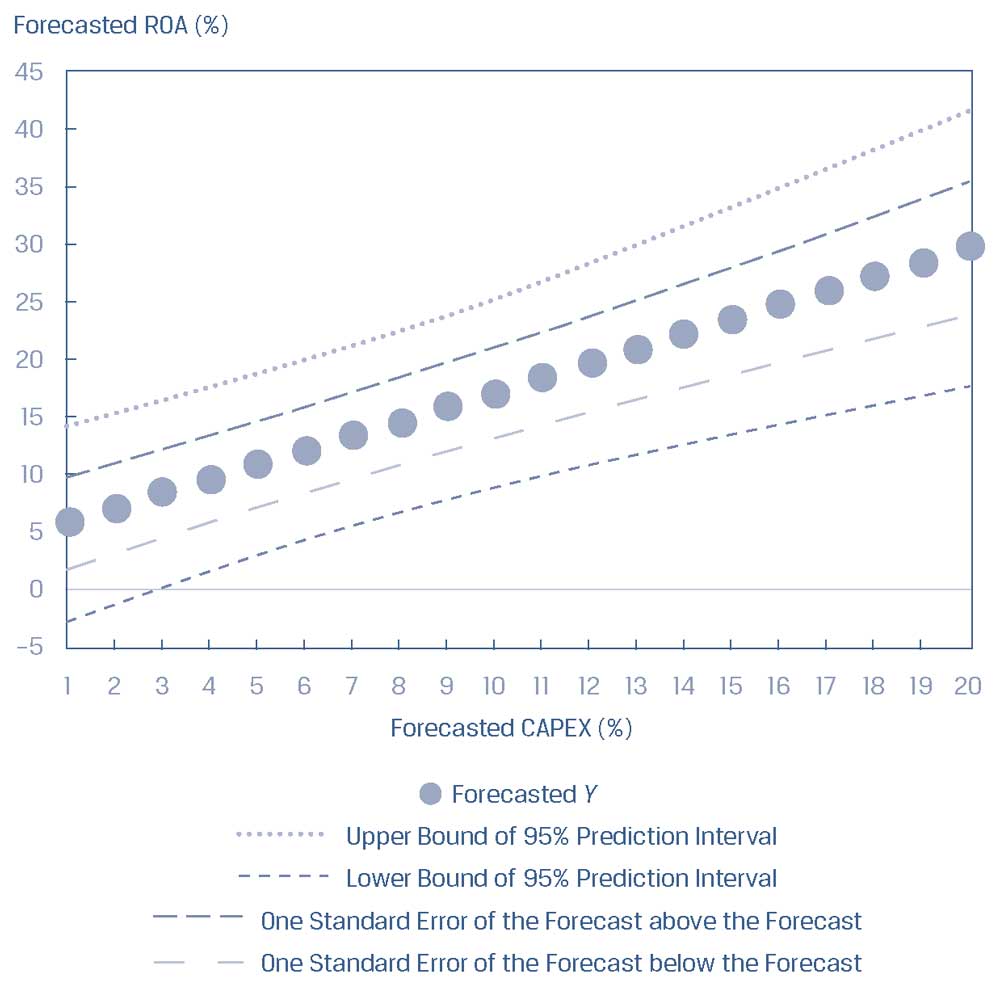
Прогнозы ROA и стандартная ошибка прогноза.
Пример 7. Прогнозирование чистой рентабельности с использованием расходов на исследования и разработки.
Предположим, мы хотим прогнозировать рентабельность по чистой прибыли компании (NPM, net profit margin) на основе ее расходов на исследования и разработки, масштабируемые ее выручкой (RDR), используя модель из Примера 2 и данные, представленные в Иллюстрации 8.
Регрессионная модель рассчитана с использованием данных о восьми компаниях следующим образом:
\( \hat Y_f = 16.5 - 1.3 X_f \).
со стандартной ошибкой оценки (\(s_e\)) 1.8618987 и дисперсией RDR 4.285714, рассчитанной по формуле
\( \dst {\sum^n_{i=1} (X_i - \overline X)^2 \over (n-1) } \).
- Каково прогнозируемое значение NPM, если прогнозируемое значение RDR составляет 5?
- Какова стандартная ошибка прогноза (\(s_f\)), если прогнозируемое значение RDR составляет 5?
- Каков 95% интервал прогнозирования для прогнозируемого значения NPM, при использовании критических t-значений (df = 6) \(\pm\)2.447?
- Каково прогнозируемое значение NPM, если прогнозируемое значение RDR составляет 15?
- Какова стандартная ошибка прогноза, если прогнозируемое значение RDR составляет 15?
- Каков 95% интервал прогнозирования для прогнозируемого значения NPM, при использовании критических t-значений (df = 6) \(\pm\)2.447?
Решение.
- Прогнозируемое значение NPM равно 10:
\( 16.5 - (1.3 \times 5) = 10 \).
- Чтобы получить стандартную ошибку прогноза (\(s_f\)), мы сначала должны рассчитать дисперсию RDR. После этого у нас есть все значения для расчета \(s_f\):
\( \dst \sum^n_{i=1} (X_i - \overline X)^2 = 4.285714 \times 7 = 30 \).
\( s_f = 1.8618987
\dst \sqrt{1+ {1 \over 8} + {(5-7.5)^2 \over 30} } = 2.1499 \).
- 95% интервал прогнозирования для прогнозируемого значения NPM составит:
\( \Bigl\{ 10 \pm 2.447(2.1499) \Bigr\} \)
\( \Bigl\{ 4.7392 < \hat Y_f < 15.2608 \Bigr\} \)
- Прогнозируемое значение NPM равно -3:
\( 16.5 - (1.3 \times 15) = -3 \).
- Чтобы получить стандартную ошибку прогноза, мы сначала должны рассчитать изменение RDR. После этого мы можем рассчитать \( s_f \):
\( \dst \sum^n_{i=1} (X_i - \overline X)^2 = 4.285714 \times 7 = 30 \).
\( s_f = 1.8618987
\dst \sqrt{1+ {1 \over 8} + {(15-7.5)^2 \over 30} } = 3.2249 \).
- 95% интервал прогнозирования для прогнозируемого значения NPM составит:
\( \Bigl\{ -3 \pm 2.447(3.2249) \Bigr\} \)
\( \Bigl\{ -10.8913 < \hat Y_f < 4.8913 \Bigr\} \)
