CFA - Проверка гипотез о коэффициентах линейной регрессии
Рассмотрим проверку гипотез о коэффициентах линейной регрессии: точке пересечения (константе) и коэффициенте наклона, когда независимая переменная является индикаторной переменной, - в рамках изучения количественных методов по программе CFA (Уровень II).
Проверка гипотез о точке пересечения (константе) линейной регрессии.
Есть случаи, когда мы хотим проверить, соответствует ли точка пересечения (константа) совокупности линейной регрессии конкретному значению.
В качестве напоминания о том, как интерпретировать точку пересечения (константу), рассмотрим простую линейную регрессию, где темп роста выручки компании является зависимой переменной (\(Y\)), а темп роста ВВП страны, в которой работает компания, является независимой переменной (\(X\)).
Точка пересечения (константа) - это темп роста выручки компании, при котором темп роста ВВП составляет 0%.
Формула расчета стандартной ошибки точки пересечения, \(s_{\hat b_0}\):
\( s_{\hat b_0} =
\dst \sqrt { {1 \over n} +
\dst { \overline X^2 \over \sum^n_{i=1} (X_i - \overline X )^2 } }
\) (17)
Мы можем проверить, отличается ли точка пересечения от гипотетического значения \(B_0\), путем сравнения оценочного значения точки пересечения \(\hat b_0\) с ее гипотетическим значением, а затем делением разницы на стандартную ошибку точки пересечения:
\( t_{\text{константа}} =
\dst {\hat b_0 - B_0 \over s_{\hat b_0} } =
\dst {\hat b_0 - B_0 \over \dst \sqrt { {1 \over n} +
\dst { \overline X^2 \over \sum^n_{i=1} (X_i - \overline X )^2 } } }
\)
В примере регрессии ROA константа (точка пересечения) составляет 4.875%. Предположим, мы хотим проверить, превышает ли константа 3%.
Односторонняя проверка этой гипотезы показана в Иллюстрации 27.
Как видите, мы отвергаем нулевую гипотезу. Другими словами, есть достаточные доказательства того, что при отсутствии капитальных затрат (CAPEX = 0), ROA больше 3%.
Иллюстрация 27. Проверка гипотезы о точке пересечения для регрессии ROA по CAPEX.
|
Шаг 1 |
Сформулируйте гипотезы. |
\(H_0 : b_0 \leq 3\% \) против \(H_{\alpha} : b_0 > 3\% \) |
|
Шаг 2 |
Определите соответствующий статистический критерий. |
\( t_{\text{константа}} = \dst {\hat b_0 - B_0 \over s_{\hat b_0} } \) с \(6 – 2 = 4\) степенями свободы. |
|
Шаг 3 |
Установите уровень значимости. |
\(\alpha\) = 5%. |
|
Шаг 4 |
Укажите правило решения. |
Критическое t-значение = 2.132. Мы отклоняем нулевую гипотезу, если рассчитанная t-статистика больше 2.132. |
|
Шаг 5 |
Рассчитайте статистический критерий. |
\( t_{\text{константа}} = \dst {4.875 - 3.0 \over \dst \sqrt{ {1 \over 6} + {6.1^2 \over 122.64} } } = {1.875 \over 0.68562} = 2.73475 \) |
|
Шаг 6 |
Примите решение. |
Отклоните нулевую гипотезу. Есть достаточно доказательств, чтобы утверждать, что точка пересечения (константа) больше 3%. |
Проверка гипотез о наклоне регрессии, когда независимая переменная является индикаторной переменной.
Предположим, мы хотим выяснить, влияют ли ежеквартальные объявления о прибыли компании на доходность ее акций.
В этом случае мы могли бы использовать индикаторную или фиктивную переменную (англ. 'indicator variable', 'dummy variable'), которая принимает только значения 0 или 1 в качестве независимой переменной.
Рассмотрим пример ежемесячной доходности акций компании за 30-месячный период.
Моделью простой линейной регрессии для решения этого вопроса будет ежемесячная доходность (RET), регрессированная по индикаторной переменной (EARN), которая приобретает значение 0, если в данном месяце не было объявления о прибыли, и 1, если было объявление о прибыли:
\( {\rm RET}_i = b_0 + b_1 {\rm EARN}_i + \epsilon_i \)
Эта регрессионная модель позволяет нам проверить, существуют ли разные показатели месячной доходности для месяцев, в которые была объявлена прибыль по сравнению с месяцами, в которые не было объявления о прибыли.
Наблюдения и результаты регрессии показаны графически в Иллюстрации 28.
Иллюстрация 28. Объявления о прибыли, фиктивная переменная и доходность акций.
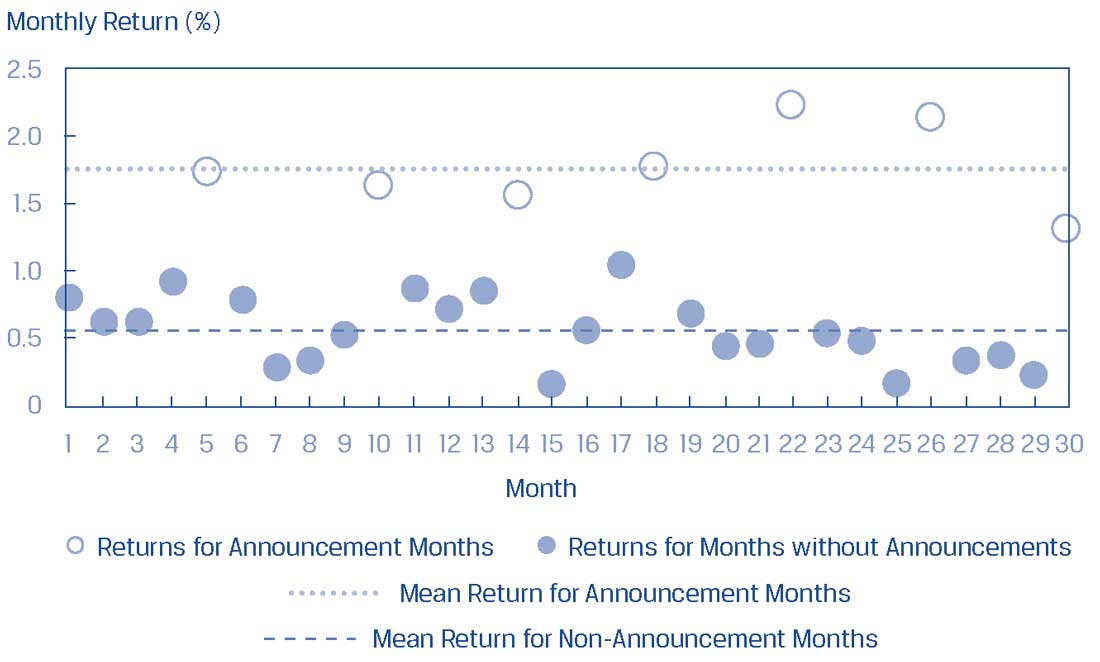
Объявления о прибыли, фиктивная переменная и доходность акций.
Очевидно, что есть несколько месяцев, в которых доходность отличается от других месяцев, и они соответствуют месяцам, в которые была объявлена прибыль.
Мы оцениваем простую линейную регрессию и выполняем проверку гипотез таким же образом, как если бы независимая переменная была непрерывной переменной.
В простой линейной регрессии точка пересечения интерпретируется как прогнозируемое значение зависимой переменной, при котором индикаторная переменная равна нулю.
Кроме того, коэффициент наклона, при котором индикаторная переменная равна 1, является разностью средних значений, если мы сгруппируем наблюдения по индикаторной переменной. Результаты регрессии приведены в Таблице A Иллюстрации 29.
Иллюстрация 29. Регрессия и проверка различий с использованием индикаторной переменной.
А. Результаты оценки регрессии.
|
Оценочные коэффициенты |
Стандартная ошибка коэффициентов |
Расчетный статистический критерий |
|
|---|---|---|---|
|
Точка пересечения |
0.5629 |
0.0560 |
10.0596 |
|
EARN |
1.2098 |
0.1158 |
10.4435 |
Степени свободы = 28.
Критические t-значения = +2.0484 (значимость 5%).
B. Проверка различий в средних значения.
|
RET для месяцев, в которых была объявлена прибыль |
RET для месяцев, в которых не было объявления прибыли |
Разница в средних значениях |
|
|---|---|---|---|
|
Среднее значение |
1.7727 |
0.5629 |
1.2098 |
|
Дисперсия |
0.1052 |
0.0630 |
|
|
Наблюдения |
7 |
23 |
|
|
Суммарная дисперсия |
0.07202 |
||
|
Расчетный статистический критерий |
10.4435 |
Степени свободы = 28.
Критические t-значения = +2.0484 (значимость 5%).
Мы можем выяснить следующее из Таблицы A Иллюстрации 29:
- Точка пересечения (0.5629) - это среднее значение доходности за месяцы, в которые не было объявления прибыли.
- Коэффициент наклона (1.2098) - это разница средних значений доходности для месяцев, когда была объявлена прибыль, и когда не было объявления прибыли.
- Мы отвергаем нулевую гипотезу о том, что коэффициент наклона по EARN равен нулю. Мы также отвергаем нулевую гипотезу о том, что точка пересечения равна нулю. Причина в том, что в обоих случаях рассчитанный статистический критерий превышает критическое F-значение.
Мы также можем проверить, является ли средняя ежемесячная доходность одинаковой как для месяцев с объявлением прибыли, так и для месяцев без объявления прибыли, выполнив следующую проверку гипотезы:
\(Н_0 : \mu_{RET \text{с объявлением}} = \mu_{RET \text{без объявления}} \)
и
\(Н_{\alpha} : \mu_{RET \text{с объявлением}} \neq \mu_{RET \text{без объявления}} \)
Результаты этой проверки гипотезы взяты из Таблицы B Иллюстрации 29.
Как вы можете видеть, мы отклоняем нулевую гипотезу о том, что нет никакой разницы в среднем значении RET для месяцев с объявлением и без объявления прибыли, на уровне значимости 5%, поскольку рассчитанный статистический критерий (10.4435) превышает критическое значение (2.0484).
