CFA - Функциональные формы простой линейной регрессии
Рассмотрим функциональные формы простых линейных регрессий, которые включают преобразование независимых и зависимых переменных с помощью логарифма, - в рамках изучения количественных методов по программе CFA (Уровень II).
Не каждый набор независимых и зависимых переменных имеет линейную связь. На самом деле, мы часто видим нелинейные взаимосвязи в экономических и финансовых данных.
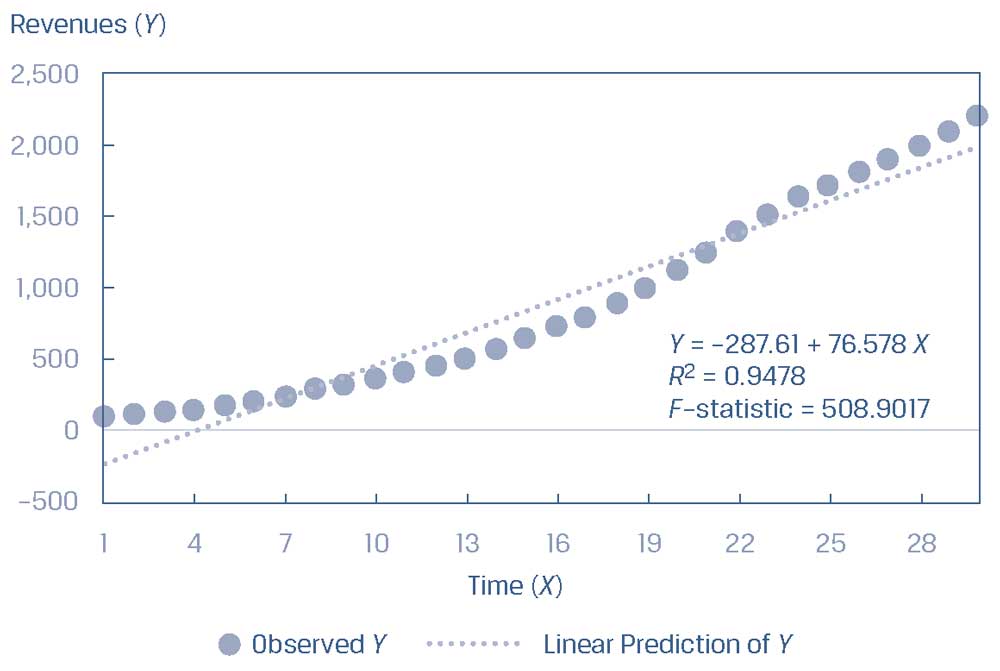
Рассмотрим выручку компании за множество периодов, как показано в Иллюстрации 33, где выручка представлена в качестве зависимой переменной (\(Y\)), а периоды в качестве независимой переменной (\(X\)). Выручка растет на 15% в год в течение нескольких лет, но затем темпы роста снижаются до 5% в год.
Оценка этой связи в качестве простой линейной модели занизила бы зависимую переменную (выручку) для некоторых диапазонов независимой переменной (периодов) и завысила бы ее для других диапазонов независимой переменной.
Иллюстрации 33. Выручка компании за периоды.
Мы все же можем использовать модель простой линейной регрессии, но нам нужно изменить либо зависимые, либо независимые переменные, чтобы она работала хорошо.
Этот подход применим ко множеству различных финансовых или экономических данных, которые вы можете использовать в качестве зависимых и независимых переменных в вашем регрессионном анализе.
Существует несколько различных функциональных форм, которые можно использовать для потенциального преобразования данных, чтобы обеспечить их использование в линейной регрессии.
Эти преобразования включают в себя использование логарифма (то есть натурального логарифма) зависимой переменной, логарифма независимой переменной, обратного значения независимой переменной, квадрата независимой переменной или дифференцирования независимой переменной.
Мы проиллюстрируем и обсудим три часто используемые функциональные формы, каждая из которых включает в себя преобразование с помощью логарифма:
- Модель log-lin, в которой зависимая переменная является логарифмической, а независимая переменная является линейной;
- Модель lin-log, в которой зависимая переменная является линейной, а независимая переменная является логарифмической; и
- Модель log-log, в которой как зависимая, так и независимая переменная представлены в логарифмической форме.
Модель log-lin.
В модели log-lin зависимая переменная находится в логарифмической форме, а независимая переменная не находится, как показано уравнении:
\( \dstl \ln Y_i = b_0+ b_1 X_i \). (21)
Коэффициент наклона в этой модели является относительным изменением зависимой переменной для абсолютного изменения независимой переменной.
Мы можем преобразовать переменную \(Y\) (доходы) из Иллюстрации 33 в ее натуральный логарифм (ln), а затем подобрать линию регрессии, как показано в Иллюстрации 34.
Из этого графика мы видим, что модель log-lin является более подходящей моделью, чем модель простой линейной регрессии.
Иллюстрация 34. Применение модели Log-Lin к выручке компании за ряд периодов.
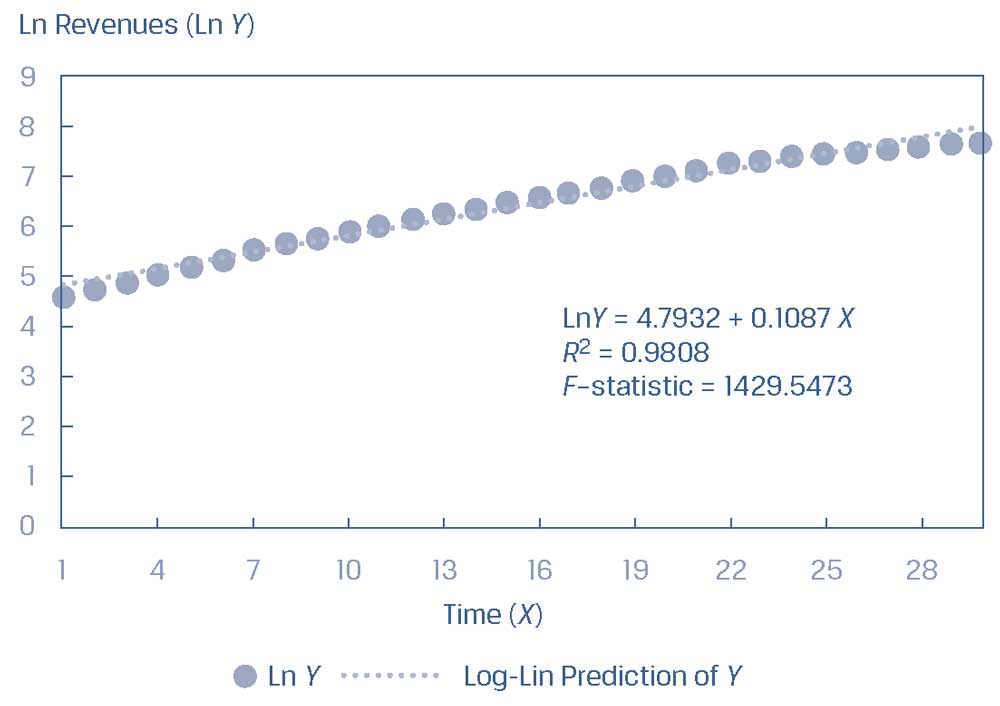
Применение модели Log-Lin к выручке компании за ряд периодов.
Важно отметить, что, работая с моделью log-lin, вы должны проявлять осторожность при прогнозировании.
Например, предположим, что моделью регрессии является
\( \ln Y = -7 + 2X \).
Если \(X\) составляет 2.5%, то прогнозируемое значение \( \ln Y \) составляет -2. В этом случае прогнозируемое значение \( Y \) является антилогарифмом -2 или \( e^{-2} = 0.135335 \).
Другое предостережение заключается в том, что вы не можете напрямую сравнивать модель log-lin с моделью lin-lin (то есть регрессия \(Y\) по \(X\) без какого-либо преобразования), потому что зависимые переменные не находятся в одной форме. Нам придется преобразовать \(R^2\) и F-статистику, чтобы выполнить корректное сравнение.
Модель lin-log.
Модель lin-log аналогична модели log-lin, но отличается тем, что только независимая переменная находится в логарифмической форме:
\( \dstl Y_i = b_0+ b_1 \ln X_i \). (22)
Коэффициент наклона в этой регрессионной модели обеспечивает абсолютное изменение зависимой переменной для относительного изменения независимой переменной.
Предположим, что аналитик изучает перекрестную взаимосвязь между операционной рентабельностью, которую отражает зависимая переменная \(Y\), и объемом продаж, который отражает независимая переменная \(X\).
Он собирает соответствующие данные по выборке из 30 компаний.
Точечный график и линия регрессии для этих наблюдений показаны в Иллюстрации 35.
Хотя наклон отличается от нуля на уровне 5% (рассчитанная t-статистика по наклону составляет 5.8616, по сравнению с критическими t-значениями \(\pm\)2.048) при \(R^2 = 55.10\%\), вопрос заключается в том, возможна ли более подходящая модель, если мы используем другую функциональную форму.
Иллюстрация 35. Взаимосвязь между операционной рентабельностью и объемом продаж.
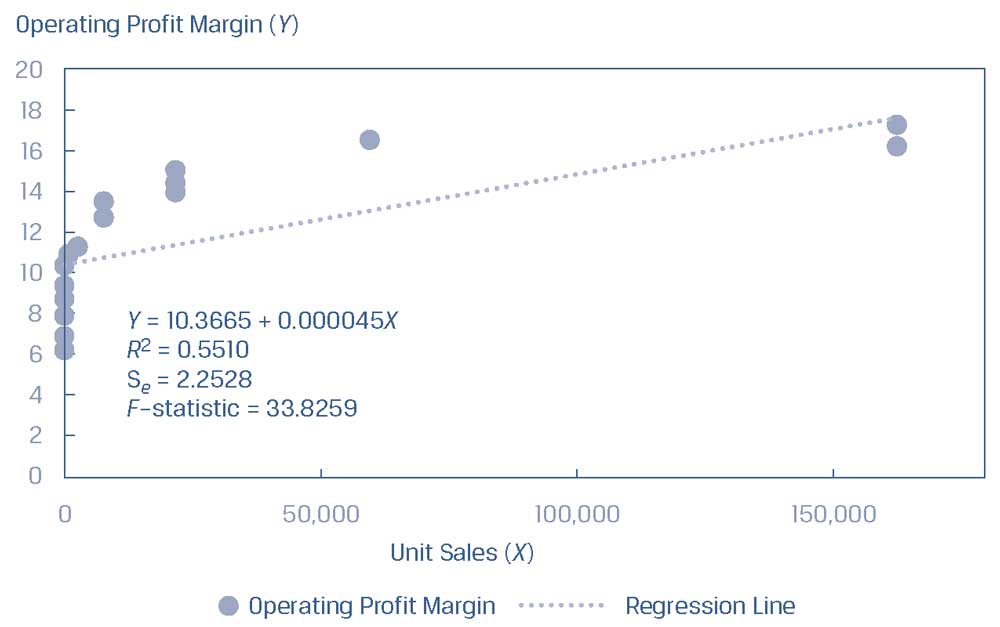
Взаимосвязь между операционной рентабельностью и объемом продаж.
Если вместо этого мы используем в нашей модели натуральный логарифм объема продаж в качестве независимой переменной, мы получим совершенно другую картину, как показано в Иллюстрации 36.
\(R^2\) для модели операционной рентабельности, регрессирующей по натуральному логарифму объема продаж, увеличивается до 97.17%.
Поскольку зависимая переменная одинакова как в исходной, так и в преобразованной модели, мы можем сравнить стандартную ошибку оценки: 2.2528 с исходной независимой переменной и гораздо более низкое значение 0.5629 с преобразованной независимой переменной.
Очевидно, что логарифмически трансформированная объясняющая (независимая) переменная привела к более подходящей модели.
Иллюстрация 36. Взаимосвязь между операционной рентабельностью и натуральным логарифмом объема продаж.
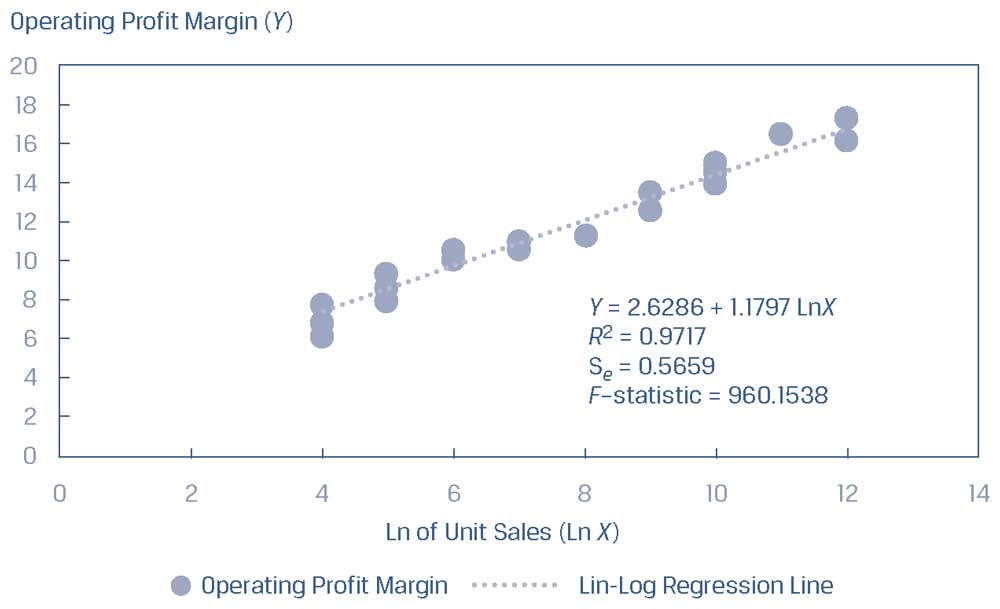
Взаимосвязь между операционной рентабельностью и натуральным логарифмом объема продаж.
Модель log-log.
Модель log-log, в которой как зависимая переменная, так и независимая переменная являются линейными в своих логарифмических формах, также называется моделью двойного логарифма (double-log model).
Эта модель полезна при расчете эластичности, поскольку коэффициент наклона является относительным изменением зависимой переменной для относительного изменения в независимой переменной.
Рассмотрим перекрестную модель выручки компании (переменная \(Y\)), регрессирующую по расходам на рекламу в процентах от расходов на продаж, а также общих и административных расходов, ADERT (переменная \(X\)).
Как показано в Иллюстрации 37, модель простой линейной регрессии приводит к поверхностной линии регрессии с коэффициентом детерминации всего 20.89%.
Иллюстрация 37. Подбор линейной связи между выручкой и рекламными расходами.
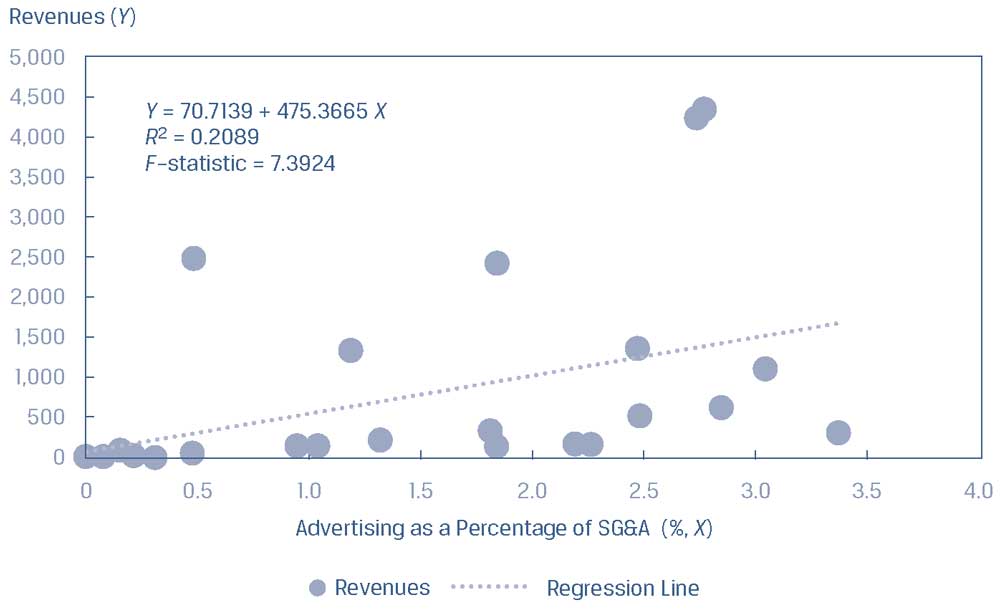
Подбор линейной связи между выручкой и рекламными расходами.
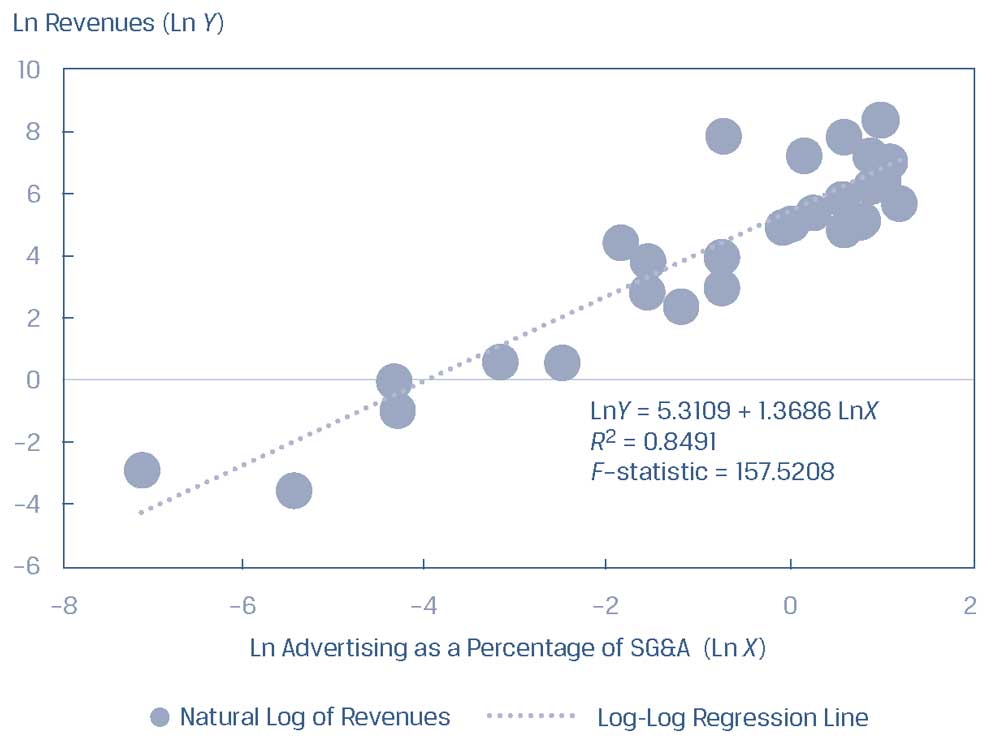
Однако, если вместо этого мы используем натуральные логарифмы как для выручки, так и для ADVERT, мы получим совершенно другую картину этой взаимосвязи.
Как показано в Иллюстрации 38, построенная линия регрессии имеет значительный положительный наклон; \(R^2\) модели log-log увеличился более чем в четыре раза, с 20.89% до 84.91%; а F-статистика подскочила с 7.39 до 157.52.
Таким образом, использование log-log преобразования значительно улучшает соответствие модели регрессии нашим данным.