CFA - Введение в анализ временных рядов и проблемы работы с временными рядами
Рассмотрим концепцию временных рядов данных и фундаментальные вопросы анализа временных рядов при принятии финансовых и инвестиционных решений, - в рамках изучения количественных методов по программе CFA (Уровень II).
Как финансовые аналитики, мы часто используем данные временных рядов для принятия инвестиционных решений.
Временные ряды данных (англ. 'time series') - это набор наблюдений за переменной в разные периоды времени: например, ежеквартальные продажи у конкретной компании в течение последних пяти лет или ежедневная доходность ценной бумаги.
В этом чтении мы исследуем две главные модели временных рядов: объяснение прошлого и предсказание будущего. Мы обсудим, как оценивать модели временных рядов, а также, как модель, описывающая конкретный временной ряд, может измениться со временем.
Следующие два примера иллюстрируют некоторые вопросы, которые мы могли бы задать о временных рядах.
Предположим, что сейчас начало 2020 года, и мы управляем американским инвестиционным портфелем, который включает в себя швейцарские акции.
Поскольку ценность этого портфеля уменьшится, если швейцарский франк обесценится по отношению к доллару, и наоборот (при прочих равных), мы рассматриваем вопрос о том, следует ли хеджировать воздействие на портфель изменения стоимости франка.
Чтобы разобраться в принятии этого решения, мы решаем смоделировать временной ряд обменного курса франк/доллара. В Иллюстрации 1 показаны ежемесячные данные по обменному курсу франк/доллар. Эти данные представляют собой ежемесячные средние значения ежедневных обменных курсов.
- Был ли обменный курс более стабильным, начиная с 1987 года, чем в предыдущие годы?
- Показал ли обменный курс долгосрочную тенденцию?
- Как мы можем наилучшим образом использовать прошлые обменные курсы для прогнозирования будущих обменных курсов?
Иллюстрация 1. Обменный курс швейцарского франка к доллару США, ежемесячные средние значения.
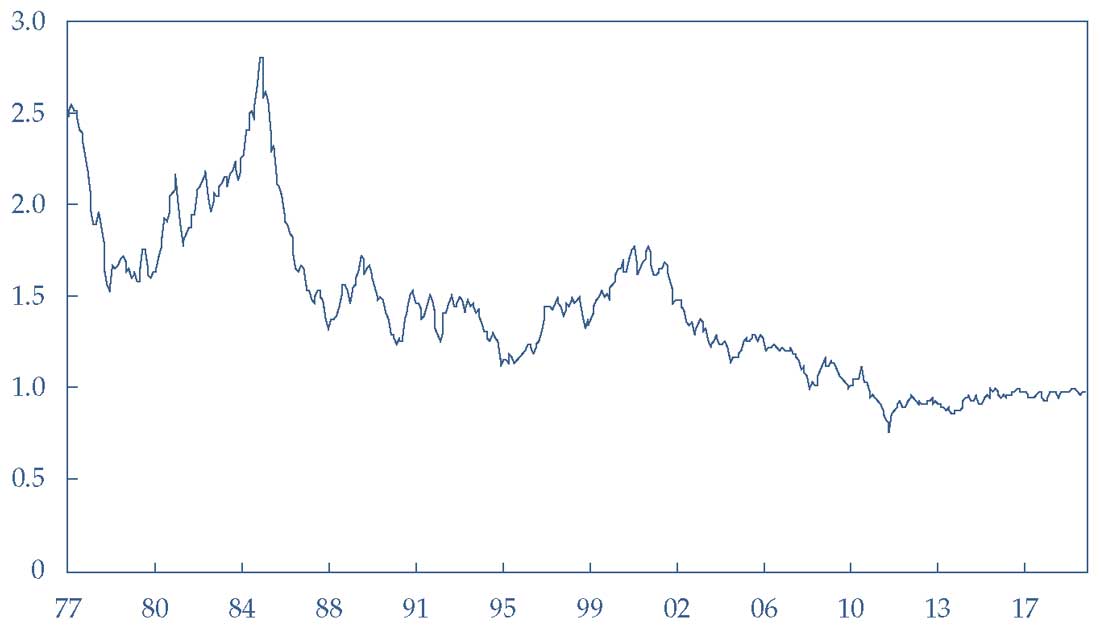
Обменный курс швейцарского франка к доллару США, ежемесячные средние значения.
Источник: Совет управляющих ФРС США.
В качестве другого примера предположим, что сейчас начало 2020 года. Мы анализируем розничные магазины по заказу компании-ритейлера и хотим предсказать розничные продажи на предстоящий год.
В Иллюстрации 2 показаны ежемесячные данные о розничных продажах в США.
Данные не скорректированы с учетом сезонности, поэтому на графике видны резкие скачки в течение праздничного сезона на рубеже каждого года.
Поскольку продажи в финансовых отчетах магазинов не скорректированы с учетом сезонности, мы моделируем розничные продажи без этой корректировки.
- Как мы можем моделировать тенденцию в розничных продажах?
- Как мы можем скорректировать экстремальную сезонность, которая выражается на графике в пиках и впадинах, встречающихся через регулярные промежутки времени?
- Как мы можем наилучшим образом использовать прошлые розничные продажи для прогнозирования будущих розничных продаж?
Иллюстрация 2. Ежемесячные розничные продажи в США.
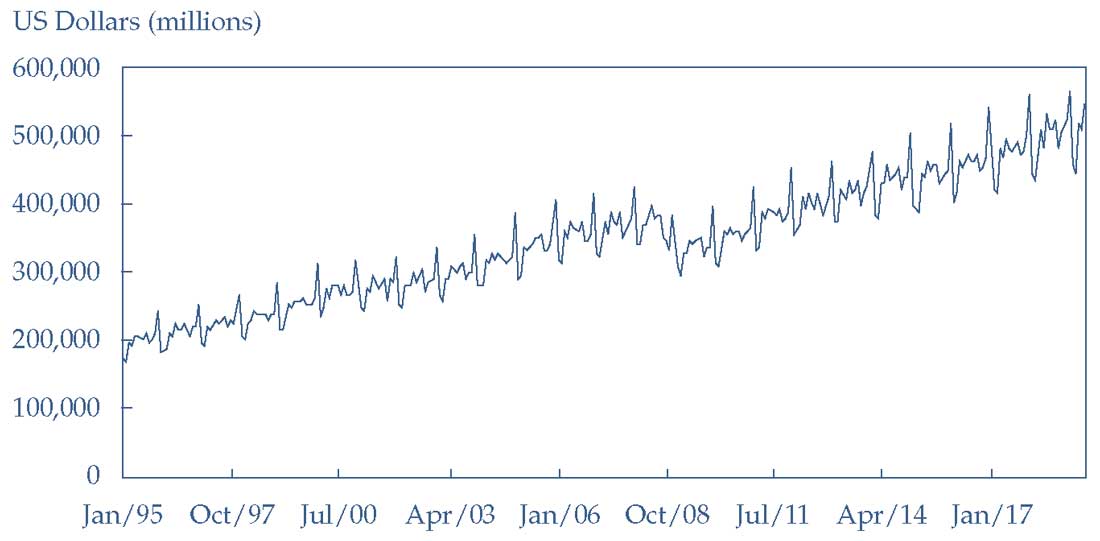
Ежемесячные розничные продажи в США.
Источник: Министерство торговли США.
При анализе временных рядов возникют некоторые фундаментальные вопросы:
- Как мы моделируем тенденции?
- Как мы прогнозируем будущие значения временных рядов на основе прошлых значений?
- Как мы моделируем сезонность?
- Как мы выбираем подходящую модель временных рядов?
- И как мы можем моделировать изменения во временных рядах с течением времени?
Мы решаем каждый из этих вопросов в этом чтении.
Сначала мы опишем типичные проблемы, возникающие при применении модели линейной регрессии к данным временных рядов. Мы представим линейные и лог-линейные модели трендов, которые описывают, соответственно, значения и натуральный логарифм значений временного ряда как линейную функцию времени.
Затем мы представим авторегрессионные модели временных рядов, которые объясняют текущее значение временных рядов с точки зрения одного или нескольких запаздывающих значений ряда.
Такие модели являются одними из наиболее часто используемых в инвестициях, и мы рассмотрим многие связанные с ними концепции и проблемы.
Затем мы уделим внимание моделям случайного блуждания. Поскольку такие временные ряды не являются ковариантно стационарными, их нельзя смоделировать с использованием авторегрессионных моделей, если они не могут быть преобразованы в стационарные временные ряды.
Поэтому мы исследуем соответствующие преобразования и проверку на стационарность.
Последующие разделы посвящены моделям временных рядов со скользящим средним, а также проблеме сезонности во временных рядах и тому, как ее решить.
Мы также изучим авторегрессионные модели со скользящим средним - более сложную альтернативу авторегрессионным моделям. Последние две темы - это моделирование изменяющейся дисперсии члена ошибки во временных рядах и последствия регрессии одного временного ряда по другому временному ряду, когда один или оба временных ряда не являются ковариантно стационарными.
Проблемы работы с временными рядами.
На протяжении всего чтения нашей целью будет применение линейной регрессии к исследуемым временным рядам.
К сожалению, при работе с временными рядами мы часто обнаруживаем, что допущения модели линейной регрессии не соблюдаются. Чтобы применить анализ временных рядов, мы должны убедиться, что допущения модели линейной регрессии соблюдены.
Когда эти допущения не соблюдаются, мы во многих случаях можем преобразовать временные ряды или определить модель регрессии иным способом, позволяющим соблюсти эти допущения.
Мы можем проиллюстрировать трудности допущений в контексте общей модели временных рядов – авторегрессионной модели.
Авторегрессионная модель (англ. 'autoregressive model') - это модель, в которой независимая переменная представляет собой запаздывающее (то есть, прошлое) значение зависимой переменной, например, модель:
\( x_t = b_0 + b_1 x_{t-1} + \epsilon_t\).
Мы также можем представить это уравнение следующим образом:
\( у_t = b_0 + b_1 y_{t-1} + \epsilon_t\).
Конкретные проблемы, с которыми мы часто сталкиваемся при работе с временными рядами, включают следующее:
1. Остаточные ошибки регрессии коррелируют.
В расчете регрессии разница между \( x_t \) и \( b_0 + b_1 x_{t-1} \) называется остаточной или необъясненной ошибкой \(\epsilon_t\) (англ. 'residual error').
Линейная регрессия предполагает, что этот член ошибки не коррелирует между наблюдениями.
Нарушение этого допущения часто оказывается более критической проблемой, если модель временных рядов включает прошлые значения временных рядов в качестве независимых переменных, по сравнению с прочими ситуациями, когда в моделях (например, моделях с перекрестными данными) зависимые и независимые переменные различны.
Как мы обсуждали в чтении о множественной регрессии, в регрессии, в которой зависимые и независимые переменные различны, сериальная корреляция ошибок не влияет на согласованность наших оценок коэффициентов точки пересечения или наклона.
Напротив, в модели с авторегрессией временных рядов, такой как \( x_t = b_0 + b_1 x_{t-1} + \epsilon_t\), сериальная корреляция в члене ошибки приводит к неспособности оценить точку пересечения (\(b_0\)) и коэффициент наклона (\(b_1\)).
2. Среднее значение или дисперсия временных рядов меняются с течением времени.
Результаты регрессии недействительны, если мы оцениваем авторегрессионную модель для временного ряда со средним значением или дисперсией, которые меняются с течением времени.
Прежде чем использовать временные ряды для прогнозирования, нам может потребоваться преобразование модели временных рядов, чтобы она была хорошо определена для линейной регрессии.
Всегда помня об этом условии, вы обнаружите, что анализ временных рядов является относительно простым и логичным.
