CFA - Модели лог-линейного тренда
Рассмотрим прогнозирование временных рядов, смоделированных как логарифмический линейный тренд, а также особенности выбора и использования модели лог-линейного тренда, - в рамках изучения количественных методов по программе CFA (Уровень II).
Иногда линейный тренд неправильно моделирует рост временных рядов. В таких случаях мы часто обнаруживаем, что подбор линейного тренда к временным ряду приводит к постоянным, а не некоррелирующим остаточным ошибкам.
Если остатки из модели линейного тренда являются постоянными, нам нужно использовать альтернативную модель, удовлетворяющую условиям линейной регрессии.
Для финансовых временных рядов важной альтернативой линейному тренду является логарифмический линейный (лог-линейный) тренд (англ. 'log-linear trend'). Лог-линейные тренды хорошо работают в подходящих временных рядах, которые имеют экспоненциальный рост.
Экспоненциальный рост означает постоянный рост с определенным темпом. Например, годовой рост с постоянным темпом 5% - это экспоненциальный рост.
Как работает экспоненциальный рост?
Предположим, мы описываем временной ряд следующим уравнением:
\(y_t = e^{b_0 + b_1 t} \), \(t=1,2, \ldots , T\), (2)
Экспоненциальный рост (англ. 'exponential growth') - это рост с постоянным темпом \( \left( e^{b_1} - 1 \right) \) и с непрерывным начислением.
Например, рассмотрим значения временного ряда за два последовательных периода. В Периоде 1 временной ряд имеет значение \(y_1 = e^{b_0 + b_1 (1)} \), а в Периоде 2 он имеет значение \(y_2 = e^{b_0 + b_1 (2)} \).
Полученное соотношение значений временных рядов в первые два периода составляет:
\( \dst y_2 / y_1 = \left( e^{b_0 + b_1 (2)} \right) \Big /
\left( e^{b_0 + b_1 (1)} \right) = e^{b_1 (1)}
\).
Как правило, в любом периоде \(t\) временной ряд имеет значение:
\(y_t = e^{b_0 + b_1 (t)} \).
В периоде \(t+1\) временной ряд имеет значение:
\(y_{t+1} = e^{b_0 + b_1 (t+1)} \).
Отношение значений в периодах \((t + 1)\) и \(t\) равно:
\( \dst y_{t+1} / y_t = \left( e^{b_0 + b_1 (t+1)} \right) \Big /
\left( e^{b_0 + b_1 (t)} \right) = e^{b_1 (1)}
\).
Таким образом, пропорциональный темп роста в течение двух последовательных периодов всегда одинаков:
\( \dst \left( y_{t+1} - y_t \right) / y_t =
y_{t+1} / y_t - 1 = e^{b_1} - 1
\).
Например, если мы используем годовые периоды и \( e^{b_1} = 1.04 \) для конкретного ряда, то эта ряд будет расти на 1.04 - 1 = 0.04 или на 4% в год.
Следовательно, экспоненциальный рост является ростом с постоянным темпом. Непрерывное начисление (темпа) - это удобный математический прием, который позволяет нам преобразовать уравнение в удобную для расчета форму.
Если мы возьмем натуральный логарифм обеих сторон Уравнения 2, то результатом будет следующее уравнение:
\(\ln y_t = b_0 + b_1 t \), \(t=1,2, \ldots , T\).
Следовательно, если временной ряд растет с экспоненциальным темпом, мы можем смоделировать натуральный логарифм этого ряда, используя линейный тренд (экспоненциальный темп роста - это непрерывное начисление темпа роста).
Иллюстрация 7 показывает результаты расчета этого уравнения.
Конечно, в реальности никакие временные ряды не растут с неизменным постоянным темпом. Следовательно, если мы хотим использовать логарифмическую (лог-линейную) модель, мы должны применить следующее уравнение:
\(\ln y_t = b_0 + b_1 t + \epsilon_t \), \(t=1,2, \ldots , T\) (3)
Обратите внимание, что это уравнение является линейным в коэффициентах \(b_0\) и \(b_1\). В отличие от модели линейного тренда, в которой прогнозируемое значение тренда \(y_t\) составляет \( \hat b_0 + \hat b_1 t\), прогнозируемое значение \(y_t\) в модели лог-линейной тренда составляет \( e^{\hat b_0 + \hat b_1 t}\), потому что \( e^{\ln y_t} = y_t\).
Изучая Формулу 3, мы видим, что лог-линейная модель предсказывает, что \( \ln y_t\) будет увеличиваться на \(b_1\) от периода к периоду. Модель предсказывает постоянный темп роста \(e^{b_1} - 1\) для \(y_t\).
Например, если \(b_1 = 0.05 \), то прогнозируемый темп роста \(y_t\) в каждом периоде составит:
\( e^{0.05} - 1 = 0.051271\) или 5.13%.
Напротив, модель линейного тренда (Уравнение 1) предсказывает, что \(y_t\) растет на постоянную величину от одного периода к другому.
Пример 2 иллюстрирует проблему неслучайных остатков в модели линейного тренда, а в Примере 3 показана логарифмическая регрессия, основанная на тех же данных.
Пример 2. Регрессия линейного тренда для квартальных продаж Starbucks.
Сейчас сентябрь 2019 года. Технологический аналитик Рэй Бенедикт хочет использовать Уравнение 1 для анализа данных о ежеквартальных продажах Starbucks Corporation, показанных в Иллюстрации 6.
Финансовый год Starbucks заканчивается в июне.
Бенедикт использует 74 наблюдения за выручкой Starbucks - со второго квартала 2001 финансового года (начинающийся с апреля 2001 года) по третий квартал 2019 финансового года (заканчивающийся в июне 2019 года) для оценки регрессионной модели линейного тренда:
\( y_t = b_0 + b_1 t + \epsilon_t \), \(t=1,2, \ldots , 74\).
Иллюстрация 6. Ежеквартальные продажи Starbucks.
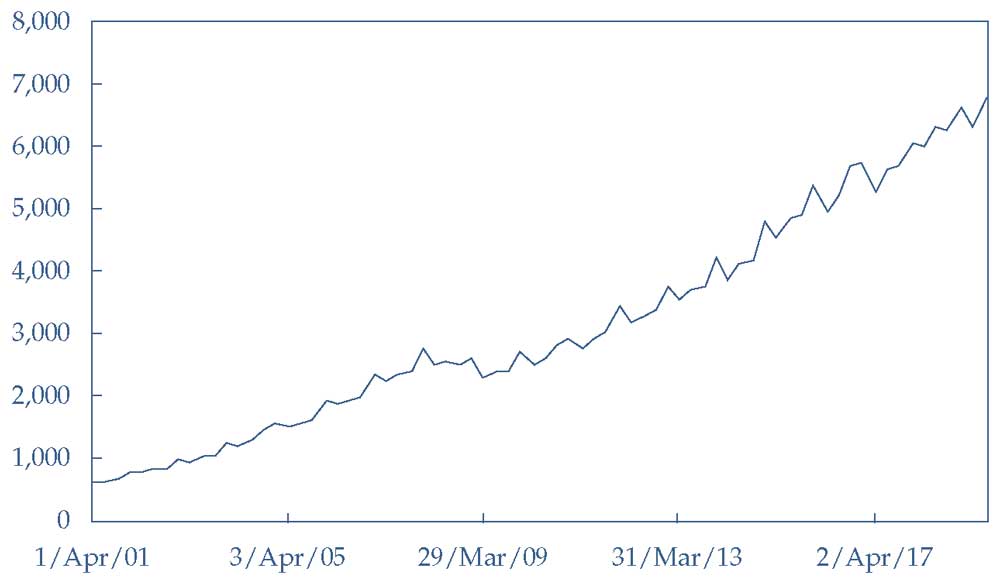
Ежеквартальные продажи Starbucks.
Источник: Bloomberg.
Иллюстрация 7. Оценка линейного тренда в продажах Starbucks.
|
\( R^2 \) |
0.9603 |
|
Стандартная ошибка |
353.36 |
|
Наблюдения |
74 |
|
Статистика Дурбина-Уотсона |
0.40 |
|
Коэффициент |
Стандартная |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
137.4213 |
82.99 |
1.6559 |
|
t (Тренд) |
80.2060 |
1.9231 |
41.7066 |
На первый взгляд, результаты, показанные в Иллюстрации 7, кажутся вполне разумными: коэффициент тренда имеет высокую статистическую значимость.
Однако, когда Бенедикт строит график данных о продажах Starbucks и линию тренда, он видит другую картину.
Как показывает Иллюстрация 8, до 2008 года линия тренда была постоянно ниже продаж. Впоследствии, до 2015 года, линия тренда была постоянно выше продаж, а затем ситуация несколько раз менялась.
Иллюстрация 8. Ежеквартальные продажи Starbucks с трендом.
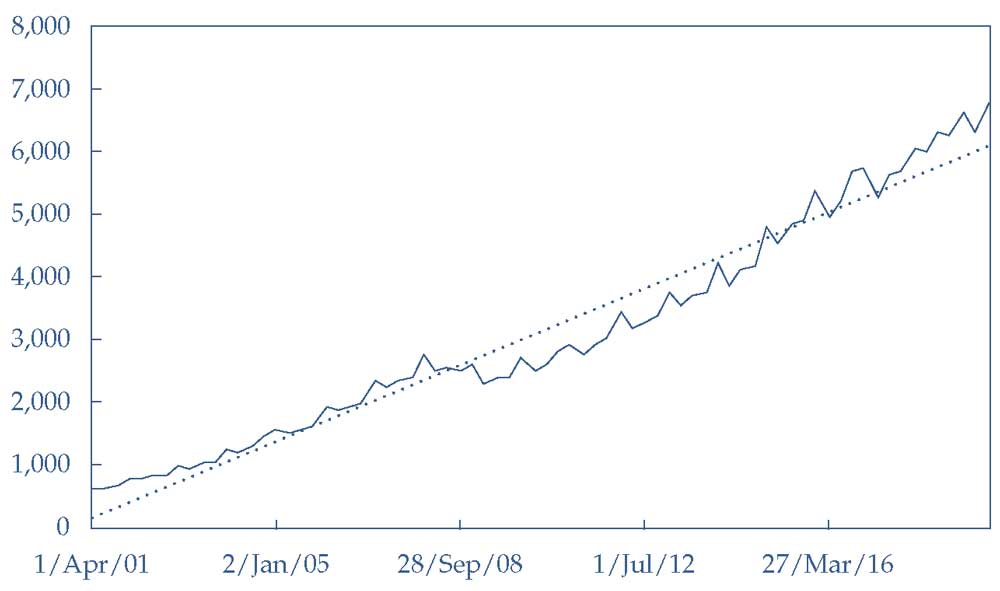
Ежеквартальные продажи Starbucks с трендом.
Источник: Bloomberg.
Вспомните ключевое допущение, лежащее в основе регрессионной модели: остаточные ошибки регрессии не коррелируют между наблюдениями.
Однако, если тренд постоянно находится выше или ниже значений временного ряда, то остатки (разница между временным рядом и трендом) сериально коррелируют.
В Иллюстрации 9 показаны остатки (разница между продажами и трендом) модели линейного тренда на основе нескорректированных данных о продажах.
График показывает, что остатки постоянны: они неизменно отрицательны с 2008 по 2015 год и неизменно положительны с 2001 по 2008 год и с 2017 по 2019 год.
Из-за этой постоянной сериальной корреляции в ошибках модели тренда, использование линейного тренда для продаж Starbucks было бы неуместным, даже если \(R^2\) уравнения является высоким (0.96).
Допущение о некоррелирующих остаточных ошибках было нарушено. Поскольку зависимые и независимые переменные не отличаются, как в регрессиях на основе перекрестных данных, это нарушение допущения является серьезной проблемой, что заставляет нас искать более подходящую модель.
Иллюстрация 9. Остаток из модели прогнозируемых продаж Starbucks с трендом.
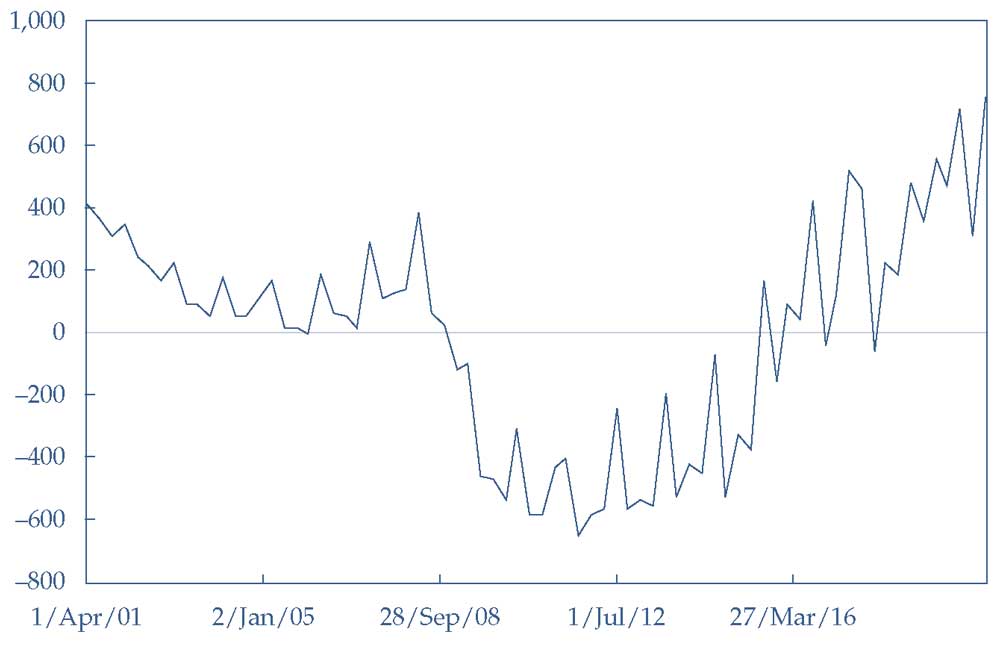
Остаток из модели прогнозируемых продаж Starbucks с трендом.
Источник: Bloomberg.
Пример 3. Лог-линейная регрессия для квартальных продаж Starbucks.
Отказавшись от модели линейного тренда, приведенной в Примере 2, технологический аналитик Бенедикт теперь пытается найти другую модель для квартальных продаж Starbucks Corporation в период со 2-го квартала 2001 года по 3-й квартал 2019 года.
Изогнутость графика данных, приведенного в Иллюстрации 6, дает намек на то, что экспоненциальная кривая может соответствовать данным. Поэтому они использует следующее линейное уравнение:
\(\ln y_t = b_0 + b_1 t + \epsilon_t \), \(t=1,2, \ldots , 74\)
Это уравнение, похоже, хорошо подходит данным о продажах. Как показывает Иллюстрация 10, \(R^2\) для этого уравнения составляет 0.95.
\(R^2 = 0.95\) означает, что 95% вариаций в натуральном логарифме продаж Starbucks объясняются исключительно линейным трендом.
Иллюстрация 10. Расчет линейного тренда для логнормального графика продаж Starbucks.
|
\( R^2 \) |
0.9771 |
|
Стандартная ошибка |
0.1393 |
|
Наблюдения |
74 |
|
Статистика Дурбина-Уотсона |
0.26 |
|
Коэффициент |
Стандартная |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
6.7617 |
0.0327 |
206.80 |
|
t (Тренд) |
0.0295 |
0.0008 |
36.875 |
Источник: Compustat.
Хотя оба Уравнения 1 и 3 имеют высокий \(R^2\), Иллюстрация 11 показывает, насколько хорошо линейный тренд соответствует натуральному логарифму продаж Starbucks (Уравнение 3).
Натуральный логарифм продаж находится очень близко к линейному тренду в течение периода выборки и не превышает или находится ниже тренда в течение длительных периодов времени.
Таким образом, логарифмическая модель тренда, кажется, лучше подходит для моделирования продаж Starbucks, чем линейная модель.
- Бенедикт хочет использовать результаты расчета Уравнения 3 для прогнозирования будущих продаж Starbucks. Каким будет прогноз продаж Starbucks на 4-й квартал 2019 года?
- Насколько отличается предыдущий прогноз от прогноза модели линейного тренда?
Решение для части 1:
Расчетное значение \( \hat b_0 \) составляет 6.7617, а расчетное значение \( \hat b_1 \) составляет 0.0295. Следовательно, в 4-м квартале 2019 года (t = 75) модель предсказывает, что
\( \ln \hat y_{75} = 6.7617 + 0.0295(75) = 8.9742 \)
и что продажи составят
\( \hat y = e^{\ln \hat y_{75} } = e^{8.9742} = \$7,896.7 \) млн.
Обратите внимание, что \( \hat b_1 = 0.0295 \) подразумевает, что экспоненциальные квартальные темпы роста продаж Starbucks составят:
\( 2.99475\% (е^{0.0464} - 1 = 0.0299475) \).
Иллюстрация 11. Натуральный логарифм квартальных продаж Starbucks.
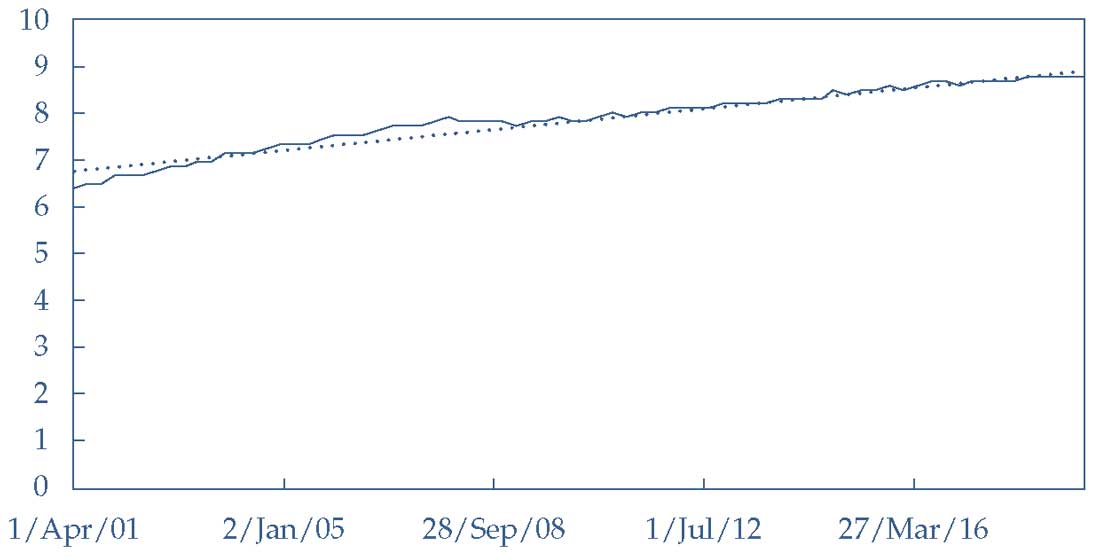
Натуральный логарифм квартальных продаж Starbucks.
Источник: Compustat.
Решение для части 2:
Иллюстрация 7 показывает, что для модели линейного тренда расчетное значение \( \hat b_0 \) составляет 137.4213, а расчетное значение \( \hat b_1 \) составляет 80.2060.
Таким образом, если мы предсказываем продажи Starbucks за 4-й квартал 2019 года (t = 75), используя модель линейного тренда, прогноз составит:
\( \hat y_{75} = 137.4213 + 80.2060(75) = \$6,152.87 \) млн.
Этот прогноз намного ниже прогноза, полученного с помощью модели логарифмической регрессии. Позже мы рассмотрим, можно ли построить лучшую модель квартальных продаж Starbucks, чем модель, которая использует только лог-линейный тренд.
