Оценка тенденции или тренда (англ. 'trend') во временных рядах и использование этого тренда для прогнозирования будущих значений временных рядов является самым простым методом прогнозирования.

Например, мы видели в Иллюстрации 2, что ежемесячные розничные продажи США являются образцом долгосрочного восходящего движения, то есть тренда. В этом разделе мы исследуем два типа трендов - линейные тренды и лог-линейные тренды, а также обсудим, как выбрать из них нужный.

Самый простой тип тенденции - это линейный тренд (англ. 'linear trend'), в котором зависимая переменная изменяется с постоянным темпом с течением времени. Если временной ряд \(y_t\) имеет линейный тренд, то мы можем смоделировать регрессию, используя следующее уравнение:

\(y_t = b_0 + b_1 t + \epsilon_t \), \(t=1,2, \ldots , T\), (1)

где

  • \(y_t\) = значение временного ряда в момент времени \(t\)  (значение зависимой переменной),
  • \(b_0\) = член точки пересечения \(y\),
  • \(b_1\) = коэффициент наклона,
  • \(t\) = время, независимая или объясняющая переменная,
  • \(\epsilon_t\) = член случайной ошибки.

В Формуле 1 линия тренда \(b_0 + b_1 t \) прогнозирует значение временных рядов в момент времени \(t\), где \(t\) принимает значение 1 в первом периоде выборки и увеличивается на 1 в каждом последующем периоде.

Поскольку коэффициент \(b_1\) является наклоном линии тренда, мы называем \(b_1\) коэффициентом тренда (англ. 'trend coefficient'). Мы можем рассчитать два коэффициента, \(b_0\) и \(b_1\), используя метод наименьших квадратов, обозначив рассчитанные коэффициенты как \(\hat b_0\) и \(\hat b_1\).

Напомним, что метод наименьших квадратов являются методом оценки, основанным на критерии минимизации суммы квадратных остатков регрессии.

Теперь мы демонстрируем, как использовать эти оценки, чтобы предсказать значение временного ряда на определенный период.

Напомним, что \(t\) приобретает значение 1 в Периоде 1. Следовательно, прогнозируемое или подобранное значение \(y_t\) для Периода 1 составляет:

\(\hat y_1 = \hat b_0 + \hat b_1(1) \).

Точно так же, в последующем периоде - скажем, Периоде 6 -  прогнозируемое значение равно:

\(\hat y_6 = \hat b_0 + \hat b_1(6) \).

Теперь предположим, что мы хотим предсказать значение временного ряда за период за пределами выборки, скажем, за период \(T + 1\). Прогнозируемое значение \(y_t\) для периода \(T + 1\) составляет:

\(\hat y_{T+1} = \hat b_0 + \hat b_1(T+1) \) .

Например, если \( \hat b_0 = 5.1 \), а \( \hat b_1 = 2 \), то при \(t = 5\) прогнозируемое значение \(y_5\) составит 15.1, а при \(t = 6\) прогнозируемое значение \(y_6\) составит 17.1.

Обратите внимание, что каждое последующее наблюдение в этом временном ряде увеличивается на \( \hat b_1 = 2 \), независимо от уровня ряда в предыдущем периоде.

Пример 1. Тенденция в индексе потребительских цен США.

Сейчас январь 2020 года. Как аналитик ценных бумаг с фиксированным доходом в трастовом отделе банка, Лизетт Миллер обеспокоена будущим уровнем инфляции и тем, как это может повлиять на стоимость портфеля.

Поэтому она хочет предсказать будущие показатели инфляции. Для этой цели она сначала должна оценить линейный тренд инфляции.

Для этого она использует ежемесячные данные Индекса потребительских цен США (CPI, US Consumer Price Index), выраженного в виде годовой процентной ставки (1% представлен как 1.0), как показано в Иллюстрации 3.

Данные включают 228 месяцев с января 1995 года по июнь 2019 года. Модель, которую необходимо оценить:

\(y_t = b_0 + b_1 t + \epsilon_t \), \(t=1,2, \ldots , 294\)

В таблице Иллюстрации 4 показаны результаты расчета этого уравнения. При 294 наблюдениях и двух параметрах эта модель имеет 292 степени свободы.

При уровне значимости 0.05 критическое значение для t-статистики составляет 1.97.

Точка пересечения \( \left( \hat b_0 = 2.7845 \right) \) является статистически значимой, поскольку значение t-статистики для коэффициента значительно выше критического значения.

Коэффициент тренда отрицательный \( \left( \hat b_1 = -0.0037 \right) \), что указывает на легкое снижение тренда инфляции в течение всего периода выборки. Однако эта тенденция не является статистически значимой, поскольку абсолютное значение t-статистики для коэффициента ниже критического значения.

Расчет уравнения регрессии можно представить как:

\( y_t = 2.7845 - 0.0037 t \).

Иллюстрация 3. Ежемесячная инфляция Индекса потребительских цен США (CPI), не скорректированная.

Ежемесячная инфляция Индекса потребительских цен США (CPI), не скорректированная.
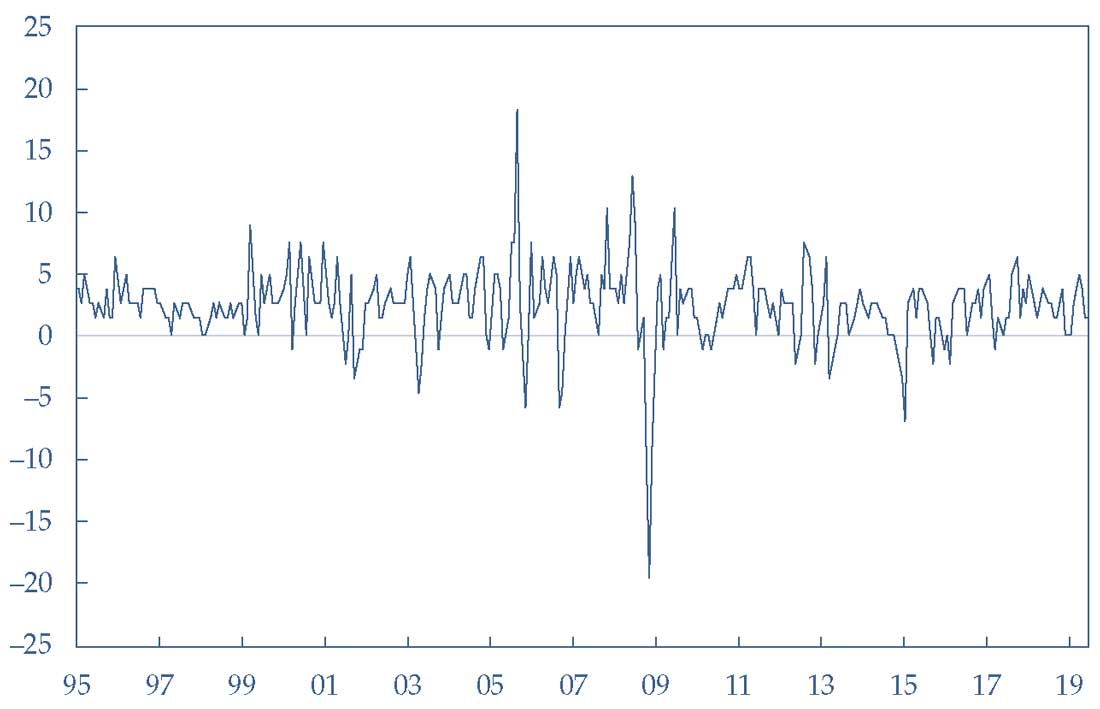
Ежемесячная инфляция Индекса потребительских цен США (CPI), не скорректированная.

Источник: Бюро статистики труда США.

Иллюстрация 4. Расчет линейного тренда инфляции: ежемесячные наблюдения, январь 1995 гогда - июнь 2019 года.

Статистики регрессии.

\( R^2 \)

0.0099

Стандартная ошибка

3.1912

Наблюдения

294

Статистика Дурбина-Уотсона

1.2145

Коэффициент

Стандартная
ошибка

t-статистика

Точка пересечения

2.7845

0.3732

7.4611

t (тренд)

-0.0037

0.0022

-1.68

Источник: Бюро статистики труда США.

Поскольку рассчитанный наклон линии тренда составил -0.0037, Миллер пришла к выводу, что наилучшей оценкой модели линейного тренда является то, что годовой уровень инфляции снижался с темпом около 37 б.п. в месяц в течение всего периода выборки.

Это снижение не статистически значимо отличается от нуля.

В январе 1995 года, в 1-й месяц выборки, прогнозируемое значение инфляции составило:

\( \hat y_1 = 2.7845 - 0.0037(1) = 2.7808\% \).

В июне 2019 года, 294-й или последний месяц выборки, прогнозируемое значение инфляции составило:

\( \hat y_{228} = 2.7845 - 0.0037(294) = 1.697\% \).

Обратите внимание, однако, что эти прогнозируемые значения относятся к периодам в рамках выборки. Сравнение этих значений с фактическими значениями показывает, насколько хорошо модель Миллер подходит для данных.

Однако основной целью этой модели является предсказание уровня инфляции для периодов вне выборки.

Например, в июне 2020 года (через 12 месяцев после окончания выборки) \( t = 294 + 12 = 306 \) прогнозируемый уровень инфляции составляет:

\( \hat y_{306} = 2.7845 - 0.0037(306) = 1.6523\% \).

В Иллюстрации 5 показаны данные об инфляции, а также установленный тренд. В соответствии с отрицательным, но малым и статистически незначительным коэффициентом тренда, установленная линия тренда немного наклонена вниз.

Обратите внимание, что инфляция, по-видимому, не движется выше или ниже линии тренда в течение длительного периода времени. Не существует постоянных различий между трендом и фактической инфляцией. Остатки (фактические значения минус значения тренда), по-видимому, непредсказуемы и некоррелируют во времени.

Таким образом, использование линии линейного тренда для моделирования показателей инфляции с 1995 по 2019 год, по-видимому, не нарушает допущений модели линейной регрессии.

Также обратите внимание, что \( R^2 \) в этой модели довольно низкий, что указывает на большую неопределенность в прогнозе инфляции с помощью этой модели. Фактически, модель объясняет только 0.99% изменений в ежемесячной инфляции.

Хотя модели линейных трендов имеют свое применение, они часто не подходят для экономических данных. Большинство экономических временных рядов отражают тенденции с изменением наклонов и/или точек пересечения с течением времени.

Линейная модель тренда идентифицирует наклон и точку пересечения, которые обеспечивают наилучшее линейное соответствие для всех прошлых данных. Отклонение модели от фактических данных может быть наибольшим в конце временного ряда данных, что может поставить под угрозу точность прогнозирования.

Позже в этом чтении мы рассмотрим, сможем ли мы построить лучшую модель инфляции, чем модель, которая использует только линию тренда.

Иллюстрация 5. Ежемесячная инфляция Индекса потребительских цен США (CPI) с трендом.

Ежемесячная инфляция Индекса потребительских цен США (CPI) с трендом.
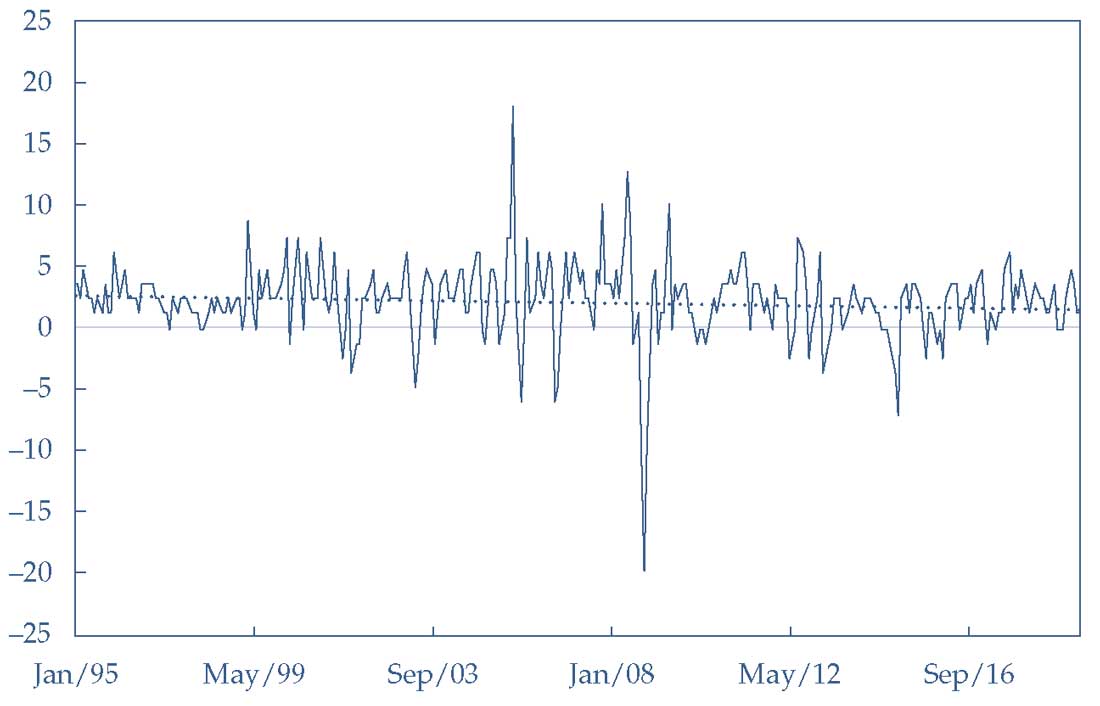
Ежемесячная инфляция Индекса потребительских цен США (CPI) с трендом.

Источник: Бюро статистики труда США.