До сих пор многие модели прогнозирования, которые мы применяли, были авторегрессионными моделями. Поскольку большинство финансовых временных рядов обладают качествами авторегрессионного процесса, авторегрессионные модели временных рядов являются, вероятно, наиболее часто используемыми моделями временных рядов в финансовом прогнозировании.

Однако некоторые финансовые временные ряды, похоже, в большей мере следуют другой разновидности моделей временных рядов, которую называют моделью скользящего среднего.

Например, как мы покажем далее, доходность индекса S&P BSE 100 можно лучше смоделировать как процесс скользящего среднего, чем как авторегрессионный процесс.

В этом разделе мы представляем основы моделей скользящего среднего, чтобы вы могли задать правильные вопросы, когда рассматриваете возможность их использования.

Сначала мы обсудим, как сгладить прошлые значения с помощью скользящего среднего, а затем как прогнозировать временные ряды, используя модель скользящего среднего. Несмотря на то, что названия обоих методов включают слова «скользящее среднее», они очень разные.

Сглаживание прошлых значений с помощью скользящего среднего n-периода.

Предположим, вы анализируете долгосрочную тенденцию в прошлых продажах компании. Чтобы сосредоточиться на этом тренде, вы можете удалить краткосрочные колебания или шум, сгладив временной ряд продаж.

Одним из методов сглаживания колебаний значений временного ряда от периода к периоду является скользящее среднее n-периода (англ. 'n-period moving average'). Скользящее среднее n-периода для текущего и прошлых \(n-1\) значений временного ряда, \(x_t\), рассчитывается как:

\( \dst {x_t + x_{t-1} + \ldots + x_{t-(n-1)} \over n} \)

Следующий пример демонстрирует, как вычислить скользящее среднее квартальных продаж AstraZeneca.

Пример 13. Квартальные продажи AstraZeneca (3).

Предположим, мы хотим вычислить скользящее среднее для 4 кварталов продаж AstraZeneca, начиная с 1 квартала 2012 года.

Продажи AstraZeneca в предыдущих четырех кварталах были следующими:

  • 1 кв. 2011, $8,490 млн.;
  • 2 кв. 2011, $8,601 млн.;
  • 3 кв. 2011, $8,405 млн.; и
  • 4 кв. 2011, $8,872 млн..

Таким образом, скользящее среднее продаж с начала 1 квартала 2012 года составляет:

(8,490 + 8,601 + 8,405 + 8,872)/4 = $8,592

Мы часто изображаем скользящее среднее временного ряда с большими колебаниями на графике, чтобы выявить закономерности в данных. В Иллюстрации 23 показаны ежемесячные розничные продажи в США с декабря 1995 года по июнь 2019 года, а также 12-месячное скользящее среднее (для расчета используются данные с января 1995 года).

Иллюстрация 23. Ежемесячные розничные продажи в США и 12-месячное скользящее среднее розничных продаж.

Ежемесячные розничные продажи в США и 12-месячное скользящее среднее розничных продаж.
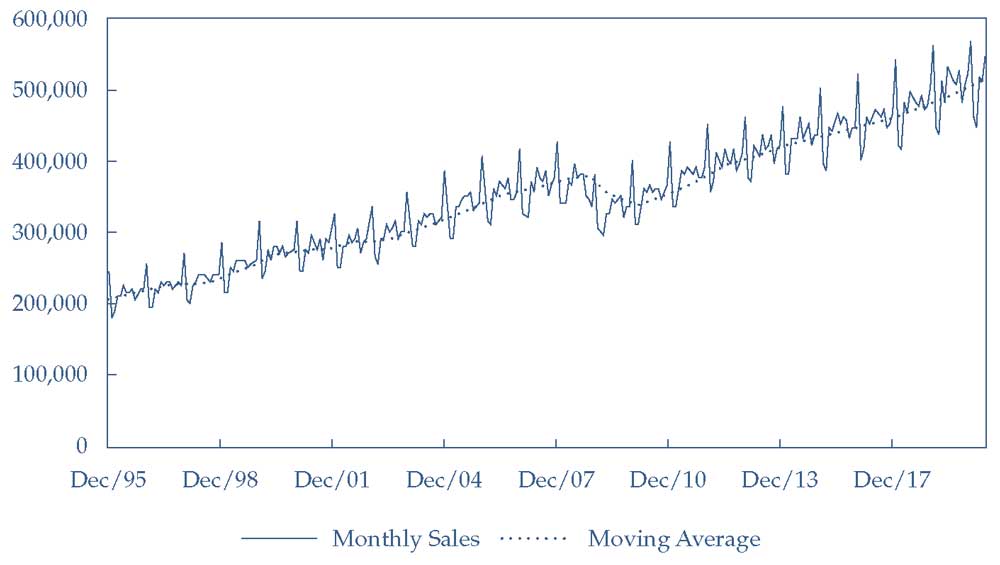
Ежемесячные розничные продажи в США и 12-месячное скользящее среднее розничных продаж.

Источник: Bloomberg.

Иллюстрация 23 показывает, что в каждом году есть очень сильный пик розничных продаж (декабрь), за которым следует резкий спад продаж (январь).

Из-за экстремальной сезонности данных 12-месячное скользящее среднее может помочь нам сосредоточиться на долгосрочных изменениях розничных продаж вместо сезонных колебаний.

Обратите внимание, что скользящее среднее не имеет резких сезонных колебаний, как в оригинальных данных розничных продаж. Скорее, скользящее среднее розничных продаж неуклонно растет, например, с 1995 по вторую половину 2008 года, а затем снижается около года, и после этого опять растет.

Эту тенденцию легче заметить, взглянув на 12-месячное скользящее среднее, а не на сам временной ряд.

Иллюстрация 24 показывает ежемесячные спотовые цены на нефть марки Брент в Европе.

Несмотря на то, что эти данные не имеют такой же резкой регулярной сезонности, как в данных розничных продаж в Иллюстрации 23, скользящее среднее сглаживает ежемесячные колебания цен на нефть, чтобы показать долгосрочные движения этих цен.

Иллюстрация 24. Ежемесячные цены на сырую нефть марки Брент в Европе и 12-месячное скользящее среднее цен.

Ежемесячные цены на сырую нефть марки Брент в Европе и 12-месячное скользящее среднее цен.
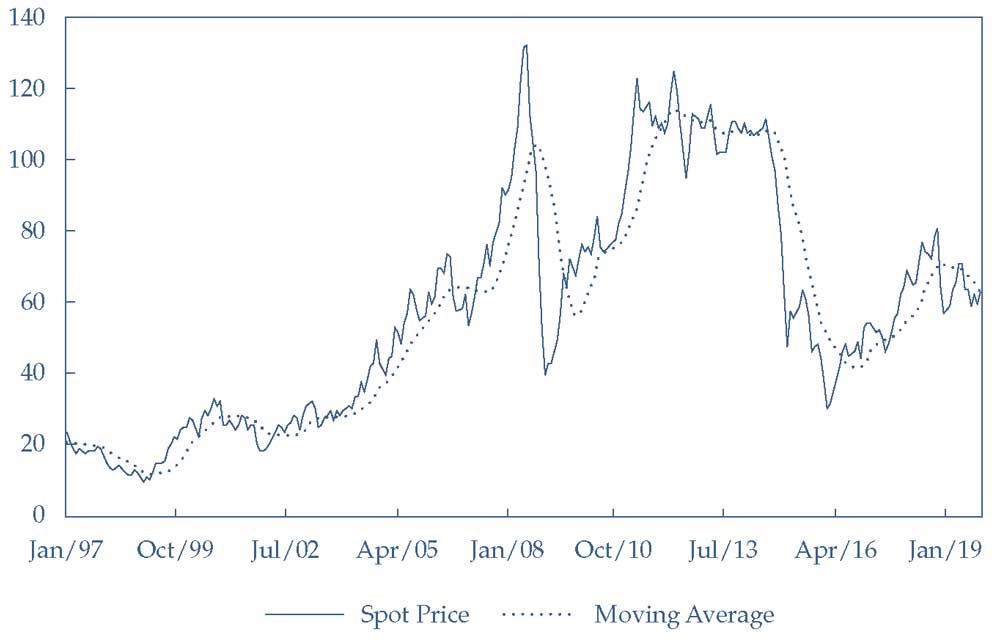
Ежемесячные цены на сырую нефть марки Брент в Европе и 12-месячное скользящее среднее цен.

Источник: Управление энергетической информации США.

Иллюстрация 24 также показывает одну слабость скользящего среднего: оно всегда отстает от больших изменений в реальных данных. Например, когда цены на нефть быстро выросли в конце 2007 года и в первой половине 2008 года, скользящее среднее выросло только постепенно.

Когда цены на нефть резко упали к концу 2008 года, скользящее среднее также отставало. Следовательно, простое скользящее среднее на основе недавнего прошлого, хотя и часто полезное для сглаживания временных рядов, может быть не лучшим предиктором будущего.

Основная причина этого заключается в том, что простое скользящее среднее придает одинаковый вес всем включенным в него периодам.

Чтобы прогнозировать будущие значения временного ряда, часто лучше использовать более сложную модель скользящего среднего. Мы обсудим такие модели ниже.

Модели скользящего среднего для прогнозирования.

Предположим, что временной ряд \(x_t\) согласуется со следующей моделью:

\(x_t = \epsilon_t + \theta \epsilon_{t-1}\), \(E (\epsilon_t) = 0 \), \(E (\epsilon^2_t) = \sigma^2 \),
\( {\rm cov} (\epsilon_t , \epsilon_s) = E (\epsilon_t  \epsilon_s) = 0\) при \( t \neq s\). (12)

Это уравнение называется моделью скользящего среднего 1 порядка или просто моделью MA(1).

Тета (\(\theta\)) является параметром модели MA(1).

Обратите внимание, что эта модель скользящего среднего очень отличается от простого скользящего среднего.

Простое скользящее среднее основано на наблюдаемых значениях временных рядов.

В модели скользящего среднего мы никогда не наблюдаем напрямую \(\epsilon_t\) или любое другое значение \( \epsilon_{t-j} \), но мы можем сделать вывод, как конкретная модель скользящего среднего будет подразумевать определенный шаблон сериальной корреляции для временного ряда, что мы обсудим далее.

Уравнение 12 - это модель скользящего среднего, потому что в каждом периоде \(x_t\) представляет собой скользящее среднее \(\epsilon_t\) и \( \epsilon_{t-1} \). Это две некоррелирующие случайные величины, каждая из которых имеет ожидаемое значение ноль.

В отличие от модели простого скользящего среднего, представленной Уравнением 11, эта модель скользящего среднего присваивает различные веса двум членам скользящего среднего (1 для \(\epsilon_t\) и \(\theta\) для \( \epsilon_{t-1} \)).

Мы можем понять, соответствует ли временной ряд модели MA(1), посмотрев на ее автокорреляции, чтобы определить, коррелирует ли \(x_t\) только с его предыдущим и следующим значениями.

Во-первых, мы исследуем дисперсию \(x_t\) из Уравнения 12 и первые две автокорреляции этой модели. Поскольку ожидаемое значение \(x_t\) составляет 0 во всех периодах, а \(\epsilon_t\) не коррелирует с собственными прошлыми значениями, первая автокорреляция не равна 0, но вторая и следующие автокорреляции равны 0.

Дальнейший анализ показывает, что в модели MA(1) все автокорреляции, за исключением первой, будут равны 0. Таким образом, для процесса MA(1) любое значение \(x_t\) коррелирует с \(x_{t-1}\) и \(x_{t+1}\), но не с другими значениями временных рядов; мы могли бы сказать, что модель MA(1) запоминает один период.

Конечно, модель MA(1) не является самой сложной моделью скользящего среднего. Модель скользящего среднего порядка \(q\), ​​обозначаемую как MA(q) и имеющую различные веса для запаздывающих членов, можно записать как:

\(x_t = \epsilon_t + \theta_1 \epsilon_{t-1} + \ldots +  \theta_q \epsilon_{t-q}  \), \(E (\epsilon_t) = 0 \), \(E (\epsilon^2_t) = \sigma^2 \),
\( {\rm cov} (\epsilon_t , \epsilon_s) = E (\epsilon_t  \epsilon_s) = 0\) при \( t \neq s\). (13)

Как мы можем определить, подходит ли модель MA(q) временному ряду?

Мы исследуем автокорреляции. Для модели MA(q) первые \(q\) автокорреляций будут значительно отличаться от 0, а все автокорреляции за пределами этого будут равны 0; модель MA(Q) имеет память о \(q\) периодах.

Этот результат имеет решающее значение для выбора правильного значения \(q\) для модели MA. Ранее мы обсуждали этот результат для отдельного случая \(q=1\), при котором все автокорреляции, за исключением первой, будут равны 0 в модели MA(1).

Как мы можем отличить авторегрессионный временной ряд от временного ряда скользящего среднего?

Напомним еще раз, мы делаем это, изучая автокорреляции самого временного ряда.

Автокорреляции большинства авторегрессионных временных рядов начинаются с больших значений и постепенно снижаются, тогда как автокорреляции MA(q) внезапно падают до 0 после первых \(q\) автокорреляций.

Мы вряд ли будем знать заранее, является ли временной ряд авторегрессионным или скользящим средним. Таким образом, автокорреляции дают нам лучшую подсказку о том, как моделировать временные ряды. Однако, большинство временных рядов лучше всего моделировать как авторегрессионную модель.

Пример 14 (исторический пример). Модель временного ряда для ежемесячной доходности индекса S&P BSE 100.

Индекс S&P BSE 100 предназначен для того, чтобы отражать доходность лучших компаний Индии с крупной капитализацией, зарегистрированных на бирже BSE Ltd. (ранее Бомбейская фондовая биржа).

Имеет ли ежемесячная доходность S&P BSE 100 автокорреляцию?

Если это так, мы можем разработать инвестиционную стратегию, использующую автокорреляции.

Какова подходящая модель для месячной доходности S&P BSE 100?

В Иллюстрации 25 показаны первые шесть автокорреляций доходности S&P BSE 100, использующие месячные данные с января 2000 года по декабрь 2013 года. Обратите внимание, что все автокорреляции довольно малы.

Имеют ли они значимость?

При 168 наблюдениях критическое значение для t-статистики в этой модели составляет около 1.98 на уровне значимости 0.05. Ни одна из автокорреляций не имеет t-статистику, большую по абсолютному значению, чем критическое значение 1.98.

Следовательно, мы не можем отвергнуть нулевую гипотезу о том, что эти автокорреляции по отдельности не отличаются существенно от 0.

Иллюстрация 25. Годовая ежемесячная доходность индекса S&P BSE 100, январь 2000 года - декабрь 2013 года.

Автокорреляции

Задержка
(Временной лаг)

Автокорреляция

Стандартная
ошибка

t-статистика

1

0.1103

0.0772

1.4288

2

-0.0045

0.0772

-0.0583

3

0.0327

0.0772

0.4236

4

0.0370

0.0772

0.4793

5

-0.0218

0.0772

-0.2824

6

0.0191

0.0772

0.2474

Наблюдения

168

Источник: BSE Ltd.

Если доходность S&P BSE 100 является моделью MA(q), то первые \(q\) автокорреляций должны значительно отличаться от 0. Однако, ни одна из автокорреляций не является статистически значимой, поэтому доходность S&P BSE 100 не соответствует MA(0).

Модель MA(0), для которого мы допускаем, что среднее значение является ненулевым, принимает следующую форму:

\(x_t = \mu + \epsilon_t \), \(E (\epsilon_t) = 0 \), \(E (\epsilon^2_t) = \sigma^2 \),
\( {\rm cov} (\epsilon_t , \epsilon_s) = E (\epsilon_t  \epsilon_s) = 0\) при \( t \neq s\). (14)

Это означает, что временные ряды не являются предсказуемыми. Этот результат не должен быть удивительным, потому что большинство исследований предполагают, что краткосрочную доходность фондовых индексов трудно предсказать.

На основании теории и практики инвестиций мы ожидаем, что средняя месячная доходность S&P BSE 100 положительна (\( \mu > 0\)). Мы также можем обобщить Уравнение 13 для временного ряда MA(q), добавив постоянный член \(\mu\).

Включение постоянного термина в модель скользящего среднего не меняет выражения для дисперсии и автоковариаций временного ряда.

Ряд ранних исследований рынков со слабой доходностью использовал Уравнение 14 в качестве модели доходности акций. См. Garbade (1982).

Из этого примера мы видим, как изучение автокорреляций позволяет нам выбирать между моделями AR и MA.

Если бы доходность индекса S&P BSE 100 соответствовала модели AR(1), то первая автокорреляция значительно бы отличалась от 0, а автокорреляция постепенно снижалась.

Однако даже первая автокорреляция значительно не отличается от 0. Поэтому мы можем быть уверены, что доходность S&P BSE 100 соответствует модели AR(1) или любой другой модели AR более высокого порядка.

Этот вывод согласуется с нашим выводом о том, что S&P BSE 100 соответствует модели MA (0).