CFA - Тест временного ряда на нестационарность
Рассмотрим концепцию единичного корня, анализ временных рядов с единичным корнем, а также проверку авторегрессионной модели на нестационарность с помощью теста (критерия) единичного корня, - в рамках изучения количественных методов по программе CFA (Уровень II).
Ранее мы обсудили, как использовать концепции случайного блуждания, чтобы определить, являются ли временные ряды ковариантно стационарными.
Этот подход фокусируется на коэффициенте наклона в случае модели AR(1) случайного блуждания с дрейфом, в отличие от традиционного подхода к рядам с автокорреляцией, который мы обсудим далее.
Исследование автокорреляции временных рядов при различных временных лагах (запаздываниях) является известным приемом для выяснения того, являются ли временные ряды стационарными.
Как правило, для стационарных временных рядов либо автокорреляции для всех лагов статистически неотличимы от нуля, либо автокорреляции быстро падают до нуля, по мере увеличения количества лагов до больших значений.
И наоборот, автокорреляции нестационарных временных рядов не демонстрируют эти характеристики. Тем не менее, этот подход менее определенный, чем более популярный тест на нестационарность, известный как тест (критерий) Дики-Фуллера (англ. 'Dickey-Fuller test') для единичного корня.
Мы можем объяснить то, что известно как проблема единичного корня, в контексте модели AR(1). Чтобы временной ряд из модели AR(1) был ковариантно стационарным, абсолютное значение коэффициента лага \(b_1\) должно быть менее 1.0.
Мы не можем полагаться на статистические результаты модели AR(1), если абсолютное значение коэффициента лага больше или равно 1.0, потому что временные ряды не будут ковариантно стационарными.
Если коэффициент лага равен 1.0, временной ряд имеет единичный корень (англ. 'unit root'): это означает, что ряд является случайным блужданием и не является ковариантно стационарным. Обратите внимание, что когда \(b_1\) больше 1 в абсолютном значении, мы говорим, что существует «взрывной корень» (англ. 'explosive root').
По определению, все модели случайного блуждания, с или без члена дрейфа, имеют единичные корни.
Как мы проверяем наличие единичного корня во временных рядах?
Если мы считаем, что временной ряд \(x_t\) является случайным блужданием с дрейфом, то было бы заманчиво оценить параметры модели AR(1) \(x_t = b_0 + b_1 x_{t-1} + \epsilon_t\) c использованием линейной регрессии и выполнить t-тест гипотезы о том, что \(b_1 = 1\).
К сожалению, если \(b_1 = 1\), то \(x_t\) не является ковариантно стационарным, и t-значение расчетного коэффициента \(\hat b_1\) фактически не следует t-распределению; следовательно, t-тест (t-критерий) будет недействительным.
Дики (Dickey) и Фуллер (Fuller) в 1979 году разработали тест (критерий) единичного корня на основе преобразованной версии модели AR(1):
\(x_t = b_0 + b_1 x_{t-1} + \epsilon_t\).
Вычитание \(x_{t-1}\) из обеих сторон модели AR(1) дает:
\(x_t - x_{t-1} = b_0 + (b_1 - 1) x_{t-1} + \epsilon_t\)
или
\(x_t - x_{t-1} = b_0 + g_1 x_{t-1} + \epsilon_t\),
\( E (\epsilon_t) = 0 \), (10)
где \(g_1 = (b_1 - 1)\).
Если \(b_1 = 1\), то \(g_1 = 0\) и, таким образом, тест \(g_1 = 0\) является тестом \(b_1 = 1\).
Если в модели AR(1) есть единичный корень, то \(g_1\) будет равна 0 в регрессии, где зависимая переменная является первой разностью временного ряда, а независимая переменная - это первый лаг временного ряда.
Нулевой гипотезой теста Дики-Фуллера является \(H_0 : g_1 = 0\), то есть это проверка временного ряда на наличие единичного корня и нестационарность, а альтернативная гипотеза \(H_a : g_1 < 0\) - это проверка на отсутствие временного корня и нестационарность.
Чтобы выполнить тест, нужно вычислить t-статистику для \(\hat g_1\) обычным образом, но вместо использования традиционных критических значений для t-теста, необходимо использовать пересмотренный набор значений, рассчитанных Дики и Фуллером; пересмотренные критические значения больше по абсолютному значению, чем обычные критические значения.
Некоторые программные статистические пакеты включают в себя тесты Дики-Фуллера.
Пример 11 (исторический пример). Квартальные продажи AstraZeneca (1).
В январе 2012 года аналитик по акциям Арон Берглин создает модель временных рядов для анализа квартальных продаж AstraZeneca, британско-шведской биофармацевтической компании со штаб-квартирой в Лондоне.
Он использует квартальные продажи AstraZeneca в долларах США с января 2000 года по декабрь 2011 года и запаздывающие данные о продажах до 2000 года, которые могут понадобиться для создания этой модели.
Он обнаруживает, что модель лог-линейного тренда, кажется, лучше подходит для моделирования продаж AstraZeneca, чем модель линейного тренда.
Тем не менее, статистика Дурбин-Уотсона для лог-линейной регрессии составляет всего 0.7064, что заставляет его отвергнуть гипотезу о том, что ошибки в регрессии не имеют сериальной корреляции.
Он приходит к выводу, что не может моделировать логарифм квартальных продаж AstraZeneca, используя только линию временного тренда. Он решает смоделировать логарифм квартальных продаж AstraZeneca с использованием модели AR(1).
Он использует следующую модель:
\( \ln {\rm Продажи}_t = b_0 + b_1(\ln {\rm Продажи}_{t-1}) + \epsilon_t \)
Прежде чем оценить эту регрессию, аналитик должен использовать тест Дики-Фуллера, чтобы определить, есть ли единичный корень в логарифме квартальных продаж AstraZeneca.
Если он использует выборку квартальных данных о продажах AstraZeneca с первого квартала 2000 года по четвертый квартал 2011 года, получив натуральный логарифм каждого наблюдения и рассчитав t-статистику для теста Дики-Фуллера, то значение этой статистики может заставить его не отклонять нулевую гипотезу о присутствии единичного корня в логарифме квартальных продаж AstraZeneca.
Если нам кажется, что временной ряд имеет единичный корень, то как мы должны его моделировать?
Один из методов, который часто успешно применяется, заключается в том, чтобы моделировать ряд первой разности как авторегрессионный временной ряд. Следующий пример демонстрирует этот метод.
Пример 12. Квартальные продажи AstraZeneca (2).
График логарифма квартальных продаж AstraZeneca показан в Иллюстрации 20. Изучив график, Берглин пришел к выводу, что логарифм квартальных продаж не является ковариационно стационарным (т.е., что у него есть единичный корень).
Иллюстрация 20. Логарифм квартальных продаж AstraZeneca.
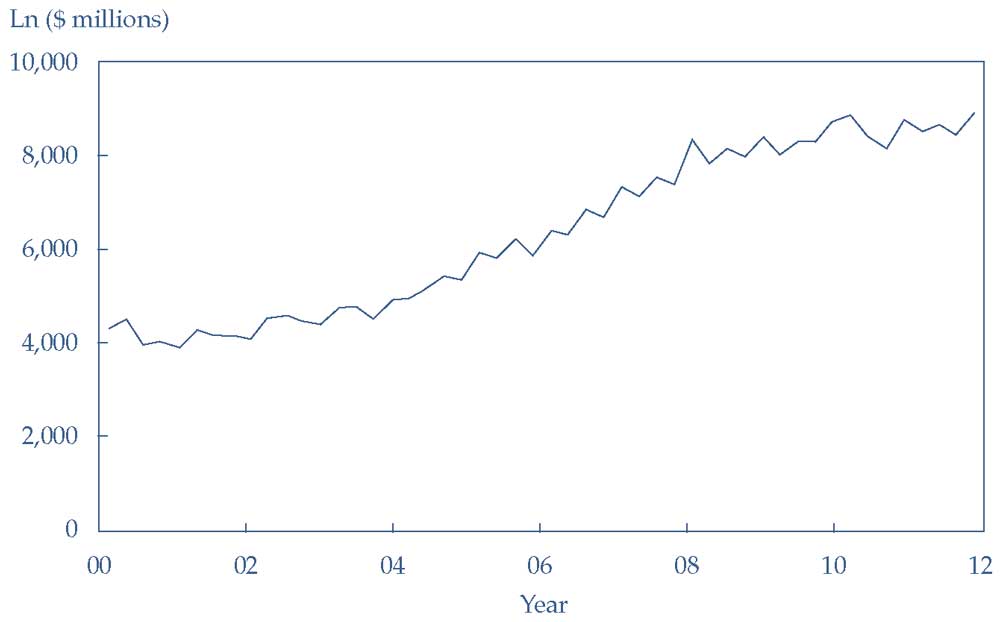
Логарифм квартальных продаж AstraZeneca.
Источник: Compustat.
Таким образом, он создает новый временной ряд, \(y_t\), который является первой разностью логарифма квартальных продаж AstraZeneca. Иллюстрация 21 показывает этот временной ряд.
Берглин сравнивает Иллюстрацию 21 с Иллюстрацией 20 и замечает, что полученный ряд первой разности устраняет сильную тенденцию к росту, которая присутствовала в логарифме продаж AstraZeneca.
Поскольку временной ряд первой разности не имеет сильного тренда, Берглин предполагает, что этот ряд является ковариантно стационарным, вместо того, чтобы предположить, что продажи AstraZeneca или логарифм продаж AstraZeneca являются ковариантно стационарными временными рядами.
Иллюстрация 21. Логарифм разности квартальных продаж AstraZeneca.
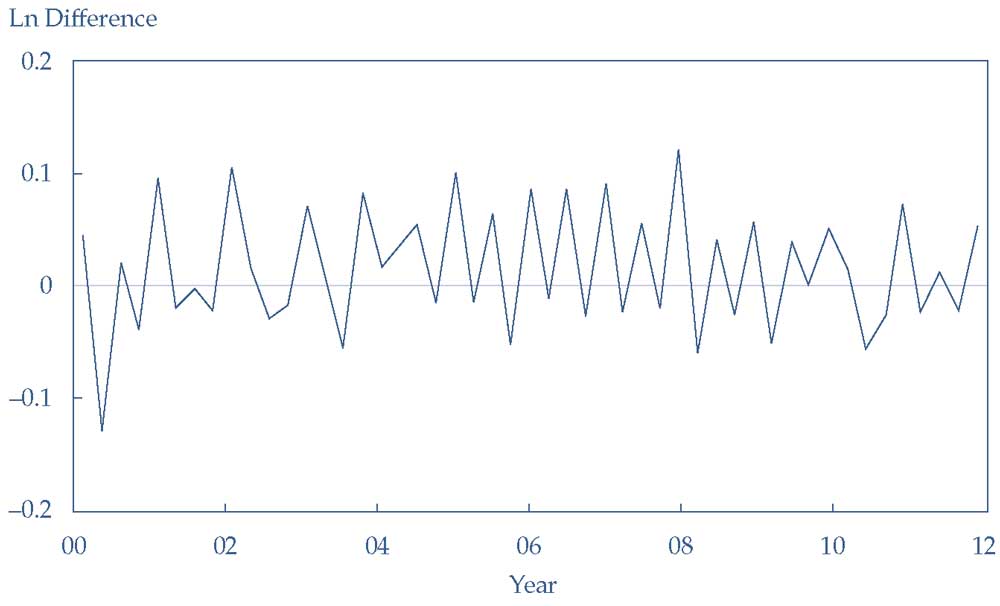
Логарифм разности квартальных продаж AstraZeneca.
Источник: Compustat.
Теперь предположим, что Берглин решил моделировать новый ряд, используя модель AR(1). Берглин использует модель:
\( \ln ({\rm Продажи}_t) - \ln ({\rm Продажи}_{t-1}) =
b_0 + b_1 [\ln ({\rm Продажи}_{t-1}) - \ln ({\rm Продажи}_{t-2})]
+ \epsilon_t \)
Иллюстрация 22 показывает результаты этой регрессии.
Иллюстрация 22. Логарифм разности продаж: Модель AR(1) квартальных наблюдений AstraZeneca, январь 2000 года-декабрь 2011 года.
|
Статистики регрессии |
|
|---|---|
|
\( R^2 \) |
0.3005 |
|
Стандартная ошибка |
0.0475 |
|
Наблюдения |
48 |
|
Статистика Дурбин-Уотсона |
1.6874 |
|
Коэффициент |
Стандартная |
t-статистика |
|
|---|---|---|---|
|
Точка пересечения |
0.0222 |
0.0071 |
3.1268 |
|
\( \ln {\rm Продажи}_{t-1} \) - \( \ln {\rm Продажи}_{t-2} \) |
-0.5493 |
0.1236 |
-4.4442 |
Автокорреляция остатков
|
Задержка |
Автокорреляция |
Стандартная |
t-статистика |
|---|---|---|---|
|
1 |
0.2809 |
0.1443 |
1.9466 |
|
2 |
-0.0466 |
0.1443 |
-0.3229 |
|
3 |
0.0081 |
0.1443 |
0.0561 |
|
4 |
0.2647 |
0.1443 |
1.8344 |
Источник: Compustat.
Нижняя часть Иллюстрации 22 предполагает, что первые четыре автокорреляции остатков в этой модели не являются статистически значимыми. При 48 наблюдениях и 2 параметрах эта модель имеет 46 степеней свободы.
Критическое значение для t-статистики этой модели выше 2.0 при уровне значимости 0.05. Ни одна из t-статистик для этих автокорреляций не имеет абсолютного значения, превышающего 2.0.
Следовательно, мы не можем отклонить нулевые гипотезы о том, что каждая из этих автокорреляций равна 0 и вместо этого заключаем, что в остатках нет существенной автокорреляции.
Этот результат предполагает, что модель хорошо определена и что мы могли бы использовать ее расчетные коэффициенты.
Как точка пересечения (\(\hat b_0 = 0.0222\)), так и коэффициент (\(\hat b_1 = -0.5493\)) по первому лагу нового временного ряда первой разности статистически значимы.
1. Объясните, как интерпретировать расчетные коэффициенты модели.
Решение для части 1:
Значение точки пересечения (0.0222) подразумевает, что, если продажи не изменились в текущем квартале (\(y_t = \ln {\rm Продажи}_t \) - \( \ln {\rm Продажи}_{t-1}\) = 0 ), то продажи вырастут на 2.22% в следующем квартале.
Однако, если продажи изменились в течение этого квартала, модель предсказывает, что продажи вырастут на 2.22% минус 0.5493 умножить на рост продаж в этом квартале.
2. Продажи AstraZeneca в третьем и четвертом квартале 2011 года составили $8,405 млн. и $8,872 млн. соответственно.
Если мы используем предыдущую модель вскоре после окончания 4 квартала 2011 года, то какой будет прогнозируемая сумма продаж AstraZeneca за 1 квартал 2012 года?
Решение для части 2:
Допустим, \(t\) - это 4 квартал 2011 года, тогда \(t-1\) - 3 квартал 2011 года, а \(t+1\) - 1 квартал 2012 года. Тогда нам придется вычислить:
\( y_{t+1} = 0.0222 - 0.5493 y_t \).
Чтобы вычислить \( \hat y_{t+1} \), нам нужно найти:
\(y_t = \ln {\rm Продажи}_t - \ln {\rm Продажи}_{t-1}\)
В 3 квартале 2011 года продажи AstraZeneca составили $8,405 млн., поэтому
\( \ln {\rm Продажи}_{t-1} = \ln 8,405 = 9.0366 \).
В 4 квартале 2011 года продажи Astrazeneca составили $8,872, млн., поэтому
\( \ln {\rm Продажи}_{t-1} = \ln 8,872 = 9.0907 \).
Таким образом,
\( y_t = 9.0907 - 9.0366 = 0.0541 \).
Поэтому
\( \hat y_{t+1} = 0.0222 - 0.5493(0.0541) = -0.0075 \).
Если \( \hat y_{t+1} = -0.0075 \), то
\( \begin{aligned}
-0.0075 &= \ln {\rm Продажи}_{t+1} - \ln {\rm Продажи}_t
&= \ln ({\rm Продажи}_{t+1} / {\rm Продажи}_t)
\end{aligned} \).
Если мы возведем в степень обе стороны этого уравнения, то получим результат:
\( \dst e^{-0.0075} = \left(
{ {\rm Продажи}_{t+1} \over {\rm Продажи}_t }
\right) \)
\( \begin{aligned}
{\rm Продажи}_{t+1} &= {\rm Продажи}_t e^{-0.0075} \\
&= \$8,872 {\rm млн.} \times 0.9925 \\
&= \$8,805 {\rm млн.}
\end{aligned} \)
Таким образом, на основе продаж в 4 квартале 2011 года эта модель предсказала бы, что продажи AstraZeneca в 1 квартале 2012 года составят $8,805 млн.
Этот прогноз продаж мог бы повлиять на наше решение о покупке акций AstraZeneca в то время.
