Одним из важных вопросов, с которыми сталкивается аналитик при моделировании временного ряда, является используемый период выборки. Оценки коэффициентов регрессии модели временного ряда могут существенно изменяться в разные периоды выборки, используемые для оценки модели.

Оценки коэффициента регрессии модели временных рядов, применяемой для более раннего периода выборки, часто могут сильно отличаться от оценки модели, оцениваемой для более позднего периода выборки.

Точно так же оценки могут отличаться при использовании относительно более коротких и более длительных периодов выборки. Кроме того, выбор модели для определенного временного ряда также может зависеть от периода выборки.

Например, модель AR(1) может быть подходящей для продажи компании в один конкретный период выборки, а модель AR(2) может потребоваться для более раннего или позднего периода выборки (или для более длительного или более короткого периода выборки).

Таким образом, выбор периода выборки является важным решением в моделировании финансовых временных рядов.

К сожалению, обычно нет четкой основы в экономической или финансовой теории для определения того, использовать ли данные из более длительного или более короткого периода выборки.

Однако мы можем получить некоторое руководство, если вспомним, что наши модели действительны только для ковариантно стационарных временных рядов.

Например, мы не должны комбинировать данные из периода, в котором были фиксированные обменные курсы с данными из периода, в котором обменные курсы были плавающими.

В эти два периода обменные курсы вряд ли будут иметь одинаковую дисперсию, поскольку обменные курсы обычно гораздо более волатильны при плавающей ставке, чем при фиксированной.

Аналогичным образом, многие аналитики считают неуместным моделировать инфляцию США или поведение процентной ставки США, начиная с 1960-х годов, в рамках одного периода выборки, поскольку в течение этого периода ФРС работала в условиях разной государственной политики.

Простой способ определить подходящие выборки для оценки временных рядов - посмотреть на графики данных до начала оценки, чтобы увидеть, выглядят ли временные ряды стационарными.

Если мы знаем, что государственная политика изменилась в определенную дату, мы также можем проверить, была ли связь временных рядов одинаковой до и после этой даты.

В следующем примере мы проиллюстрируем, как выбор более длительного и более короткого периода может повлиять на решение об использовании модели временных рядов первого или второго порядка.

Затем мы покажем, как выбор модели временных рядов (и связанных коэффициентов регрессии) влияет на наш прогноз. И, наконец, мы обсудим, какой период выборки и, соответственно, какая модель и соответствующий прогноз подходят для временного ряда, проанализированного в примере.

Пример 9. Нестабильность в моделях временных рядов инфляции США.

В Примере 6 аналитик Лизетт Миллер пришла к выводу, что инфляция Индекса потребительских цен США (CPI) ​​должна быть смоделирована как временной ряд AR(2).

Коллега изучил ее результаты и поставил под сомнение оценку единой модели временных рядов, если применять ее к инфляции США начиная с 1984 года, учитывая, что ФРС агрессивно реагировала на финансовый кризис, возникший в 2007 году.

Он утверждает, что временные ряды инфляции с 1995 по 2018 год имеют два режима или две базовые модели, генерирующие временные ряды: одна работает с 1995 по 2007 год, другая - начиная с 2008 года.

Таким образом, коллега предполагает, что Миллер нужно применять новую модель начиная с 2008 года. Опираясь на его предложение, Миллер сначала оценивает модель AR(1) для инфляции с периодом выборки с 2008 по 2018 год. Иллюстрация 16 показывает ее оценку AR (1).

Иллюстрация 16. Авторегрессия: Модель AR(1) ежемесячной инфляции CPI по годовой ставке, январь 2008 г. - декабрь 2018 г.

Статистики регрессии

\( R^2 \)

0.2536

Стандартная ошибка

3.0742

Наблюдения

132

Статистика Дурбин-Уотсона

1.8164

Коэффициент

Стандартная
ошибка

t-статистика

Точка пересечения

0.8431

0.2969

2.8397

\(\text{Инфляция}_{t-1}\)

0.5036

0.0758

6.6438

Автокорреляция остатка.

Задержка
(Временной лаг)

Автокорреляция

Стандартная
ошибка

t-статистика

1

0.0999

0.087

1.1479

2

-0.1045

0.087

-1.2015

3

-0.1568

0.087

-1.8051

4

0.0500

0.087

0.5750

Источник: Бюро статистики труда США.

Нижняя часть Иллюстрация 16 показывает, что первые четыре автокорреляции остатков из модели AR (1) довольно малы.

Ни одна из этих автокорреляций не имеет t-статистики, превышающей 1.99, критического значения для определения значимости. Следовательно, Миллер не может отвергнуть нулевую гипотезу о том, что остатки не имеют сериальной корреляции.

Модель AR(1) правильно определена для периода выборки с 2008 по 2018 год, поэтому нет необходимости оценивать модель AR(2). Этот вывод сильно отличается от того, который был получен в Примере 6 с использованием данных с 1995 по 2018 год.

В этом примере Миллер первоначально отвергла модель AR(1), потому что ее остатки демонстрировали сериальную корреляцию. Когда она использовала более крупную выборку, модель AR(2) изначально, по-видимому, соответствовала данным намного лучше, чем модель AR(1).

Насколько глубоко наш выбор периода выборки влияет на наш прогноз будущей инфляции?

Предположим, что в определенный месяц инфляция составляла 4% по годовой ставке, а за месяц до этого - 3%.

Модель AR(1), показанная в Иллюстрации 16, предсказывает, что инфляция в следующем месяце составит:

0.8431 + 0.5036(4) \(\approx\) 2.86%.

Таким образом, прогноз инфляции на следующий месяц с использованием выборки с 2008 по 2018 год составляет 2.86%. Вспомним из анализа в Примере 6, что модель AR(2) для выборки с 1995 по 2018 год прогнозирует инфляцию на следующий месяц в 2.91%.

Таким образом, использование правильно определенной модели для более короткой выборки дает прогноз инфляции на 0.05 б.п. ниже прогноза, полученного с помощью правильно определенной модели для более длительного периода выборки. Такая разница может существенно повлиять на конкретное инвестиционное решение.

Какая модель верна?

Иллюстрация 17 предлагает ответ. Ежемесячная инфляция в США была гораздо более волатильной в течение среднего промежутка периода исследования, чем в более ранние или более поздние годы. Поэтому инфляция, вероятно, не являлась ковариантно стационарной с 1995 по 2018 год.

Таким образом, мы можем разумно полагать, что данные имеют более одного режима, и Миллер должна применить отдельную модель инфляции для периода с 2009 по 2018 год, как было показано ранее.

Фактически, стандартное отклонение годового ежемесячного показателя инфляции составляет всего 2.86% в 1995-2007 годах, и 3.54% в 2008-2018 годах, в основном из-за волатильности во время кризиса 2008 года.

Как показывает пример, опыт (такой как знание изменений в государственной политики) и суждения играют важнейшую роль в определении того, как моделировать временные ряды.

Если просто полагаться на автокорреляции остатков из модели временных рядов, это не даст возможность выбрать правильный период выборки для нашего анализа.

Иллюстрация 17. Ежемесячная инфляция Индекса потребительских цен США.

Ежемесячная инфляция Индекса потребительских цен США.
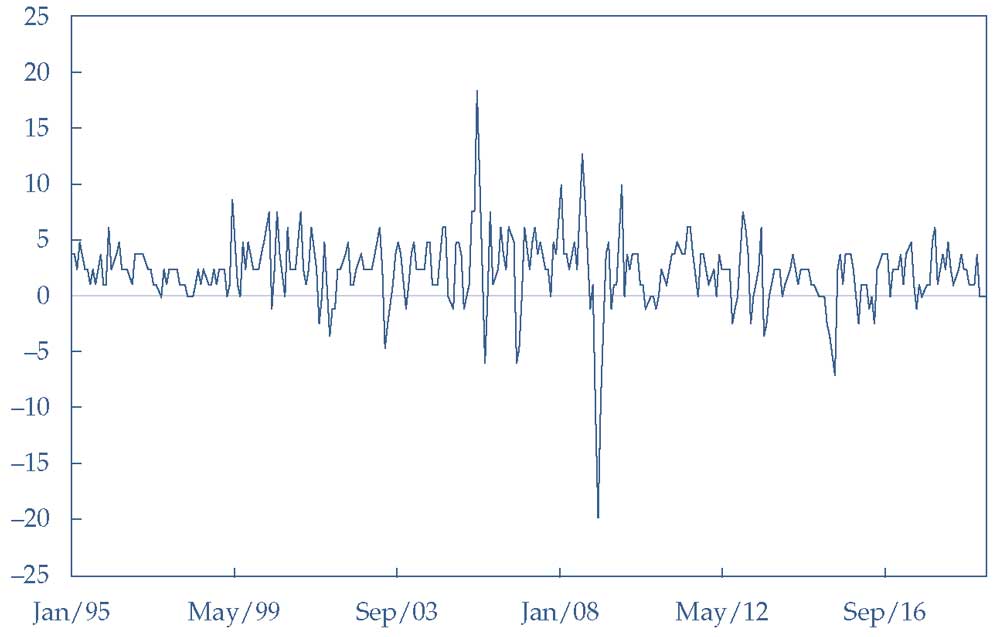
Ежемесячная инфляция Индекса потребительских цен США.

Источник: Бюро статистики труда США.