CFA - Принцип аддитивности денежного потока
В рамках изучения количественных методов финансового анализа по программе CFA рассмотрим одно из важнейших понятий временной стоимости денег - принцип аддитивности денежного потока.
Принцип аддитивности денежного потока (англ. 'cash flow additivity principle') заключается в том, что суммы денег, относящиеся к одним и тем же периодам времени (т.е. с одинаковыми индексами на временной линии), являются аддитивными.
Это - одно из важнейших понятий в математике временной стоимости денег (TVM).
Чтобы проиллюстрировать принцип аддитивности денежных потоков, рассмотрим две серии денежных потоков, изображенных на временной линии, как показано на рисунке ниже.
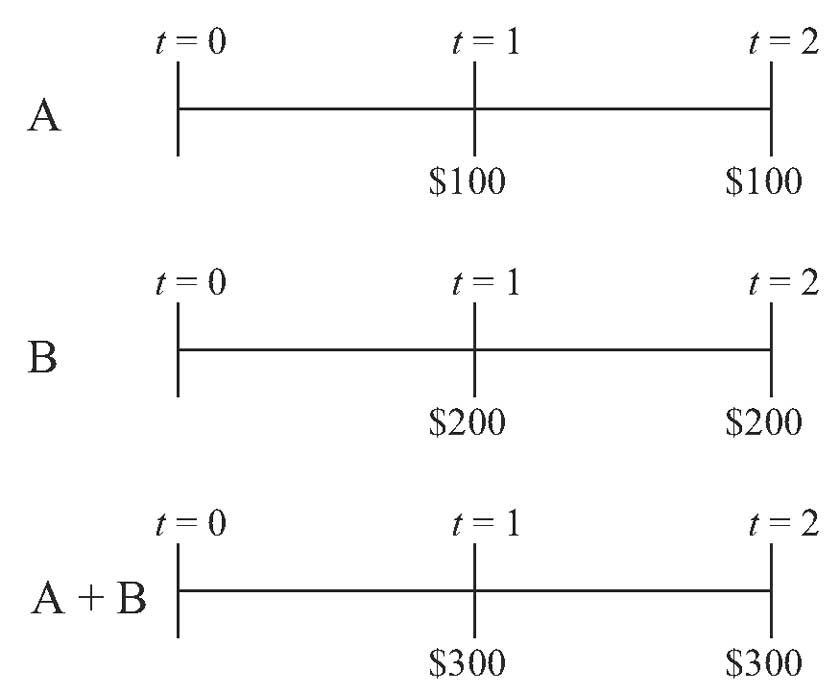 Аддитивность двух последовательностей денежных потоков.
Аддитивность двух последовательностей денежных потоков.
Серии обозначаются как A и B.
Если предположить, что годовая процентная ставка составляет 2%, мы можем найти будущую стоимость (FV) каждой серии денежных потоков следующим образом.
- Будущая стоимость серии A составляет: $100(1.02) + $100 = $202.
- Будущая стоимость серии B составляет: $200(1.02) + $200 = $404.
- Будущая стоимость совокупного потока (A + B) составляет: $202 + $404 = $606.
Альтернативный способ найти будущую стоимость - сложить денежные потоки каждой серии (т.е. A + B), а затем рассчитать будущую стоимость совокупного денежного потока, как показано на рисунке.
Третья временная линия на рисунке показывает совокупную последовательность денежных потоков.
Серия A включает денежный поток в размере $100 при \(t = 1\), а серия B включает денежный поток в размере $200 при \(t = 1\). Таким образом, объединенная серия (A + B) содержит денежный поток в размере $300 при \(t = 1\).
Мы можем таким же образом рассчитать денежный поток объединенной серии при \(t = 2\).
Будущая стоимость объединенной серии (A + B) составляет $300(1.02) + $300 = $606. Т.е., мы получили тот же результат, к которому мы пришли, когда сложили значения будущей стоимости FV для каждой серии.
Принципы аддитивности и эквивалентности также появляются в другой типичной ситуации.
Предположим, что денежные потоки составляют $4 в конце 1-го года и $24 (фактически отдельные платежи в размере $4 и $20) в конце 2-го года.
Вместо того, чтобы находить приведенную стоимость $4 за 1-й год и приведенную стоимость $24 за 2-й год, мы можем рассматривать эту ситуацию как аннуитет суммы $4 в течение 2-х лет и единовременной суммы $20 во 2-й год.
Если бы ставка дисконтирования составляла 6%, то:
- аннуитет в размере $4 имел бы приведенную стоимость $7.33;
- единовременная сумма $20 имела бы приведенную стоимость $17.80;
- совокупная приведенная стоимость составила бы $25.13.
