При оценке денежных потоков, последовательно осуществляемых в течение многих периодов времени, обычно используются следующие термины:

  • Аннуитет (англ. 'annuity') - это ограниченная последовательность (серия) денежных потоков.
  • Обычный или простой аннуитет или аннуитет постнумерандо (англ. 'ordinary annuity') - это серия денежных потоков, в которой денежные потоки происходят через 1 период, т.е. в начале следующего периода или в конце текущего периода (например, 1-й поток индексируется как \(t\) = 1).
  • Авансовый аннуитет или аннуитет пренумерандо (англ. 'annuity due') - это серия денежных потоков, в которой денежные потоки происходят немедленно, т.е. в начале текущего периода (1-й поток индексируется как \(t\) = 0).
    См. примеры расчета авансового аннуитета.
  • Бессрочный аннуитет или перпетуитет или вечная рента (англ. 'perpetuity' или 'perpetual annuity') - это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. \(t\) = 1).
    См. пример расчета перпетуитета.

Как вычислять обычный аннуитет, то есть FV равных денежных потоков?

Рассмотрим обычный аннуитет с начислением 5% годовых.

Предположим, что у нас есть 5 отдельных депозитов по $1 000, поступающих с равными интервалами, каждый из которых составляет 1 год, причем 1-й платеж происходит при \(t\) = 1.

Наша цель - найти будущую стоимость (FV) этого обычного аннуитета после внесения последнего депозита при \(t\) = 5. Поскольку все 5 депозитов вносятся с периодичностью в 1 год, последний платеж осуществляется через 5 лет.

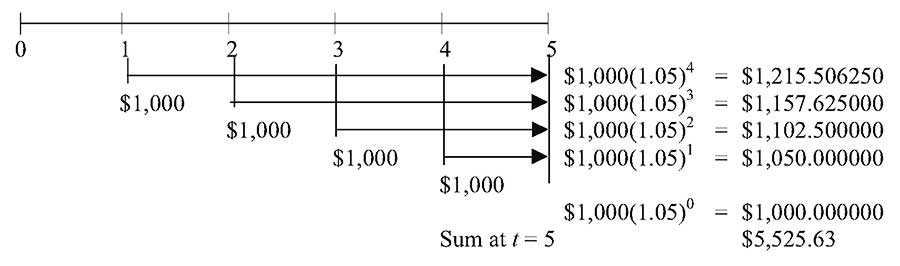Будущая стоимость (FV) пятилетнего обычного аннуитета. Будущая стоимость (FV) пятилетнего обычного аннуитета.

Как показывает временная линия на рисунке выше, мы находим будущую стоимость каждого депозита на сумму $1,000 к моменту времени \(t\) = 5, используя для каждого депозита Формулу FV (2):

\( \dstl \FV_N = \PV (1 + r)^N \)

Стрелки на рисунке выше соответствуют дате каждого депозита от даты 1-го платежа до \(t\) = 5 и указывают на расчет будущей стоимости FV для соответствующего депозита.

Например, по 1-му депозиту в размере $1 000 (при \(t\) = 1) будут начисляться проценты в течение 4-х последующих периодов.

Используя формулу FV, мы вычисляем будущую стоимость 1-го депозита при \(t\) = 5, которая составляет:

\( $1,000 (1,05)^4 = $1,215.51 \)

Для всех других платежей мы вычисляем FV аналогичным образом.

Обратите внимание, что мы находим будущую стоимость при \(t\) = 5, поэтому последний (5-й) платеж не важен и не отображается на временной линии.

Теперь, имея все значения FV при \(t\) = 5, мы можем их суммировать, чтобы получить будущую стоимость аннуитета, т.е. всей последовательности равных денежных потоков.

Эта сумма составляет $5 525,63.

Теперь рассмотрим общую формулу аннуитета, в которой:

  • \(A\) - сумма аннуитета,
  • \(N\) - количество периодов и
  • \(r\) - процентная ставка за период.

Мы можем рассчитать будущую стоимость как:

\( \begin{aligned} \dst
\FV_N &= \small A \left[(1 + r)^{N-1} + (1 + r)^{N-2} + (1 + r)^{N-3} + ... + (1 + r)^1 + (1 + r)^0 \right]
\end{aligned} \)

что можно упростить до следующей формулы:

\( \dstL \FV_N = A \left[ {(1+r)^N - 1}  \over r \right] \) (Формула 7)

Выражение в квадратных скобках - это фактор будущей стоимости аннуитета (англ. 'future value annuity factor').

Этот коэффициент означает будущую стоимость обычного аннуитета на одну денежную единицу (т.е. на $1 в нашем примере).

Умножение фактора будущей стоимости аннуитета на сумму аннуитета дает будущую стоимость обычного аннуитета.

Для обычного аннуитета, изображенного на рисунке выше, фактор будущей стоимости аннуитета из Формулы 7 можно рассчитать как:

\( \dst \left[ {(1.05)^5 - 1}  \over 0.05 \right] = 5.525631 \)

Если сумма аннуитета \(A\) = $1,000, то будущая стоимость аннуитета составляет:

$1,000 (5.525631) = $5,525.63

что соответствует вычислению, сделанному ранее.

Следующий пример иллюстрирует, как можно рассчитать будущую стоимость обычного аннуитета, используя Формулу 7.

Пример расчета будущей стоимости простого аннуитета.

Предположим, что пенсионная программа вашей компании с установленными взносами позволяет вам инвестировать до €20 000 в год. Вы планируете инвестировать €20 000 в год в индексный инвестиционный фонд в течение следующих 30 лет.

Исторически сложилось так, что этот фонд в среднем приносил своим инвесторам 9% в год.

Исходя из того, что вы будете зарабатывать 9% в год, сколько пенсионных средств будет на вашем счете после внесения последнего платежа?

Решение:

Используйте Формулу 7, чтобы найти будущую стоимость аннуитета:

\(A\) = €20,000
\(r\) = 9% = 0.09
\(N\) = 30

\( \dst \stRmL{Фактор FV}{аннуитета}
= {(1 + r)^N - 1 \over r}
= {(1.09)^30 - 1 \over 0.09} = 136.307539
\)

\( \FV_N = \€20,000 (136.307539) = \€2,726,150.77\)

Предполагая, что фонд будет зарабатывать в среднем 9% в год, вы получите €2,726,150.77 к моменту выхода на пенсию.

Как вычислять аннуитет при неравных денежных потоках?

Довольно часто последовательность денежных потоков аннуитета неравномерна. То есть, потоки денежных средств не являются одинаковыми платежами, осуществляемыми через равные периоды времени.

Это исключает использование в расчете фактора будущей стоимости аннуитета.

Например, у инвестора может быть план сбережений, который предполагает неравные денежные выплаты в зависимости от месяца года или более низкие сбережения во время запланированного отпуска.

В этом случае будущую стоимость серии неравных денежных потоков можно вычислить, рассчитав и суммировав FV каждого отдельного денежного потока.

Пример расчета аннуитета при неравномерных денежных потоках.

Предположим, что у вас есть 5 денежных потоков, которые описаны в таблице ниже. Платежи пронумерованы относительно текущей даты (\(t\) = 0).

Серия неравных денежных потоков и их будущая стоимость при ставке 5%.

Год

Денежный
поток, $

Будущая стоимость
на 5-й год

t = 1

1,000

$1,000 (1.05)4 =

$1,215.51

t = 2

2,000

$2,000(1.05)3 =

$2,315.25

t = 3

4,000

$4,000(1.05)2 =

$4,410.00

t = 4

5,000

$5,000(1.05)1 =

$5,250.00

t = 5

6,000

$6,000(1.05)° =

$6,000.00

Сумма =

$19,190.76

Все платежи, указанные в таблице выше, отличаются по сумме. Поэтому самый прямой подход к расчету будущей стоимости этих инвестиций при \(t\) = 5, - это вычисление FV каждого отдельного платежа при \(t\) = 5, а затем суммирование найденных значений FV.

Совокупная FV на 5-й год равна $19,190.76, как показано в третьем столбце таблицы.