Фактор будущей стоимости связывает сегодняшнюю текущую (приведенную) стоимость (PV, англ. 'present value') денежного потока с его будущей стоимостью (FV, англ. 'future value'). Этот коэффициент позволяет рассчитать как FV, так и PV.

Например, 5-процентная ставка приносит будущий доход в размере $105 за 1 год.

Какой должна быть текущая (первоначальная) сумма, вложенная под 5%, чтобы она выросла до $105 через 1 год?

Ответ: $100 представляют собой текущую стоимость (PV) для будущей суммы (FV) в размере $105, которая должна быть получена через 1 год, при ставке вклада 5%.

Используя будущий денежный поток, который должен быть получен в течение N периодов, и процентную ставку за период r, мы можем преобразовать Формулу (2) будущей стоимости денежного потока следующим образом:

FVN=PV(1+r)N

PV=FVN[1(1+r)N] (Формула 8)

или

PV=FVN(1+r)−N

Из Формулы 8 видно, что фактор текущей стоимости (англ. 'present value factor'), (1+r)−N является обратной величиной фактора будущей стоимости (1+r)N.

Пример расчета приведенной (текущей) стоимости денежного потока.

Страховая компания выпустила гарантированный инвестиционный сертификат (GIC), который гарантирует выплату $100 000 в течение 6 лет с 8-процентной прибылью.

Какую сумму страховщик должен инвестировать сегодня, чтобы через 6 лет обеспечить выплату обещанной суммы по сертификату?

Решение:

Мы можем применить Формулу 8, чтобы найти текущую (приведенную) стоимость, используя следующие данные:

FVN = $100,000
r = 8% = 0.08
N = 6

PV=FVN(1+r)−N=$100,000[1/(1.08)6]=$100,000(0.6301696)=$63,016.96

Можно сказать, что сегодня $63 016,96 при процентной ставке 8% эквивалентны $100 000, которые будут получены через 6 лет.

Дисконтирование сегодняшней суммы $100 000 делает будущую сумму в размере $100 000 эквивалентом $63 016,96, с учетом временной стоимости денег (TVM).

Как показывает временная линия на рисунке ниже, $100 000 дисконтированы в течение 6 полных периодов.

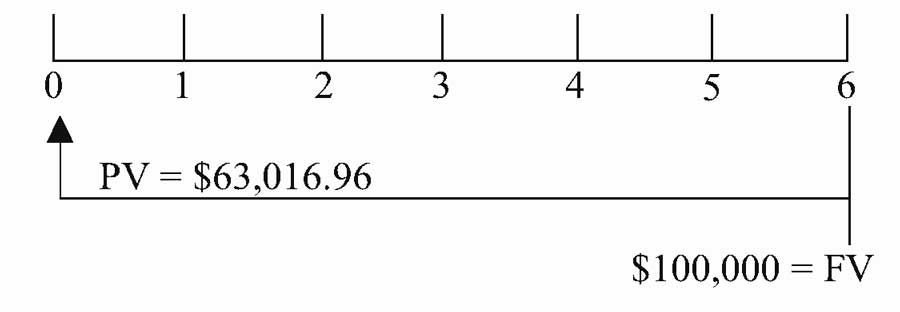Текущая стоимость (PV) $100 000 в момент времени t = 6. Текущая стоимость (PV) $100 000 в момент времени t = 6.

Пример прогнозирования приведенной стоимости денежного потока.

Предположим, что у вас есть ликвидный финансовый актив, который принесет вам $100 000 через 10 лет от текущей даты.

Ваша дочь планирует поступить в колледж через четыре года, и вы хотите знать, какова будет текущая (приведенная) стоимость актива к этому моменту.

С учетом 8% ставки дисконтирования, какова будет стоимость актива через 4 года от текущей даты?

Решение:

Стоимость актива ($100 000) - это текущая стоимость через 10 лет. При t = 4 эта сумма будет получена 6 лет спустя - см. рисунок ниже.

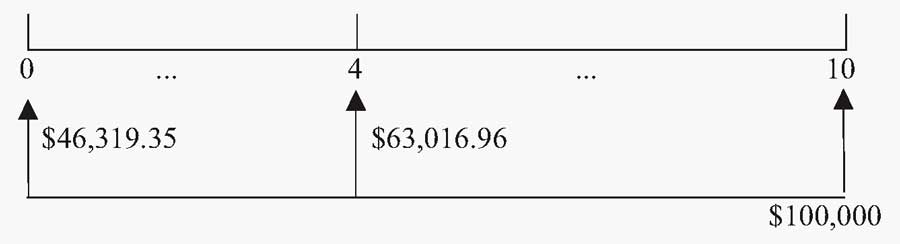Связь между текущей и будущей стоимостью актива. Связь между текущей и будущей стоимостью актива.

С помощью этой информации вы можете вычислить стоимость актива через 4 года от текущей даты, используя Формулу 8:

FVN = $100,000
r = 8% = 0.08
N = 6

PV=FVN(1+r)−N=$100,000[1/(1.08)6]=$100,000(0.6301696)=$63,016.96

Временная линия на рисунке выше показывает будущий платеж в размере $100 000, который должен быть получен при t = 10. На временной шкале также показана стоимость денежного потока при t = 4 и при t = 0.

По сравнению с суммой при t = 10, сумма при t = 4 представляет собой прогнозируемую текущую стоимость, а сумма при t = 0 является текущей приведенной стоимостью (на сегодняшний день).

Задачи, требующие вычисления приведенной стоимости (PV) требуют определения  фактора приведенной стоимости (1+r)−N.

Приведенная стоимость зависит от процентной ставки и количества периодов начисления процентов следующим образом:

  • При заданной ставке дисконтирования, чем дальше в будущем будет получена сумма, тем меньше будет текущая стоимость (PV) этой суммы.
  • Для одного и того же момента времени, с ростом ставки дисконтирования уменьшается текущая стоимость будущей суммы.

Расчет текущей (приведенной) стоимости с промежуточным начислением процентов.

Напомним, что проценты могут выплачиваться раз в полгода, ежеквартально, ежемесячно или даже ежедневно.

Для расчета процентных платежей, производимых более 1 раза в год, мы можем изменить формулу текущей стоимости (8).

Напомним, что rs - котируемая (заявленная) процентная ставка и она равна периодической процентной ставке, умноженной на количество периодов начисления в каждом году.

В целом, если в году есть более 1 промежуточного периода начисления, мы можем выразить формулу расчета текущей стоимости (PV) как:

PV=FVN(1+rsm)−mN (Формула 9)

где:

  • m = количество периодов начисления в году,
  • rs = заявленная годовая процентная ставка,
  • N = количество лет.

Формула 9 очень похожа на Формулу 8.

Как мы уже отмечали, фактор текущей (приведенной) стоимости и фактор будущей стоимости являются обратными значениями по отношению друг к другу. И добавление в формулу частоты начисления процентов не влияет на эту взаимозависимость между двумя факторами.

Единственное различие заключается в использовании периодической процентной ставки и соответствующего количества периодов начисления.

Следующий пример иллюстрирует Формулу 9.

Пример расчета текущей (приведенной) стоимость при ежемесячном начислении процентов.

Менеджер канадского пенсионного фонда знает, что фонд должен выполнить единовременный платеж в размере $5 млн. через 10 лет. Она планирует сегодня инвестировать некоторую сумму в гарантированный инвестиционный сертификат (GIC), чтобы эта инвестиция выросла до необходимой суммы в $5 млн.

Текущая процентная ставка по GIC составляет 6% в год, с ежемесячным начислением процентов.

Сколько она должна сегодня инвестировать в GIC?

Решение:

Используя Формулу 9, чтобы находим требуемую приведенную стоимость:

FVN = $5,000,000
rs = 6% = 0.06
m = 12
rs/m = 0.06/12 = 0.005
N = 10
mN = 12(10) = 120

PV=FVN(1+rsm)−mN=$5,000,000(1.005)−120=$5,000,000(0.549633)=$2,748,163.67

При применении Формулы 9 мы используем периодическую ставку (в данном случае, месячную ставку) и соответствующее количество периодов с ежемесячным начислением процентов (в данном случае 10 лет ежемесячных начислений или 120 периодов).