CFA - Кластеризация в неконтролируемом машинном обучении
Рассмотрим кластеризацию, одну из разновидностей неконтролируемого машинного обучения, а также задачи, для которых применяются алгоритмы кластеризации, - в рамках изучения количественных методов по программе CFA (Уровень II).
Кластеризация (англ. 'clustering') является еще одним типом неконтролируемого машинного обучения, который используется для сбора точек данных в аналогичные группы, называемые кластерами.
Кластер (англ. 'cluster') содержит такое подмножество наблюдений из набора данных, при котором все наблюдения в одном кластере считаются «похожими» или однородными.
Цель состоит в том, чтобы найти хорошую кластеризацию данных - это значит, что наблюдения внутри каждого кластера похожи или близки друг к другу (свойство, известное как единство или когезия [cohesion]), а наблюдения в двух разных кластерах далеки друг от друга или разнообразны (свойство, известное как разделение или сепарация [separation]) настолько, насколько возможно.
Иллюстрация 19 изображает это внутрикластерное единство и межкластерное разделение.
Иллюстрация 19. Оценка кластеризации - единство внутри кластеров и межкластерное разделение.
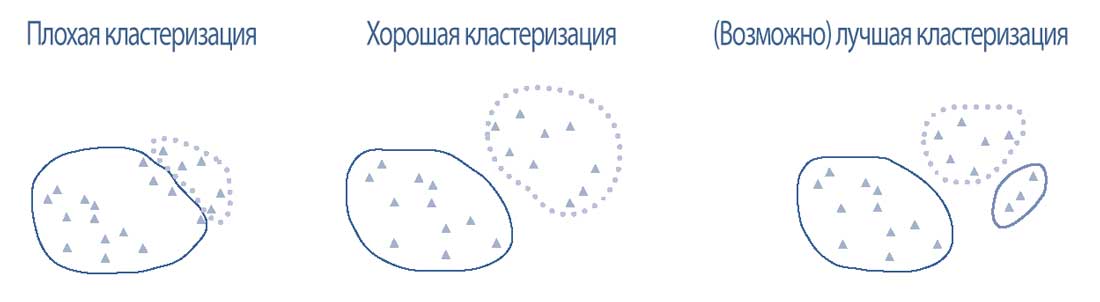
Оценка кластеризации - единство внутри кластеров и межкластерное разделение.
Алгоритмы кластеризации особенно полезны во многих инвестиционных задачах и применениях, в которых важна концепция сходства.
Например, применительно к группировке компаний, кластеризация может раскрыть важные сходства и различия между компаниями, которые не учитываются при стандартной классификации компаний по отраслям и секторам.
В управлении портфелем методы кластеризации используются для улучшения диверсификации портфеля.
На практике, экспертное человеческое суждение играет большую роль в использовании алгоритмов кластеризации.
Во-первых, нужно установить, что означает «сходство».
Каждая компания может считаться наблюдением с несколькими признаками, включая такие статьи финансовой отчетности, как общая выручка и прибыль акционеров, широкий спектр финансовых коэффициентов или любые другие потенциальные модели.
Основываясь на этих особенностях, можно определить меру сходства или «расстояние» между двумя наблюдениями (то есть компаниями). Чем меньше расстояние, тем более схожи наблюдения; чем больше расстояние, тем более разнородны наблюдения.
Обычно используемым определением расстояния является евклидово расстояние - прямолинейное расстояние между двумя точками.
Показателем расстояния тесной связи, полезным при диверсификации портфеля, является корреляция, которая представляет собой среднее евклидово расстояние между набором стандартизированных точек.
В машинном обучении регулярно используется примерно дюжина различных показателей расстояния. На практике выбор меры расстояния зависит от характера данных (числовые данные или нет) и исследуемой бизнес-задачи.
После определения соответствующей меры расстояния аналогичные наблюдения можно сгруппировать вместе.
Теперь мы изучим два наиболее популярных подхода к кластеризации:
