CFA - Кластеризация k-средних
Рассмотрим кластеризацию k-средних, один из алгоритмов неконтролируемого машинного обучения, а также задачи, для которых она подходит, - в рамках изучения количественных методов по программе CFA (Уровень II).
K-средние (k-means) - это алгоритм, который многократно разбивает наблюдения на фиксированное количество \(k\), непересекающихся кластеров.
Количество кластеров \(k\) является гиперпараметром модели (т.е. параметр, значение которого должно быть установлено исследователем до начала обучения модели).
Каждый кластер характеризуется его центроидом (centroid), то есть центром, и алгоритм относит каждое наблюдение к кластеру в соответствии с центроидом, к которому это наблюдение является наиболее близким.
Примечательно, что как только кластеры сформируются, между ними не будет определенных взаимосвязей.
Алгоритм k-средних следует итеративному процессу. Это показано в Иллюстрации 20 для \(k=3\) и набора наблюдений переменной, которую можно описать двумя признаками.
В Иллюстрации 20 горизонтальные и вертикальные оси графика представляют собой, соответственно, первый и второй признаки.
Например, инвестиционный аналитик может захотеть сгруппировать набор фирм в три группы в соответствии с двумя численными показателями качества управления компанией. Алгоритм группирует наблюдения на следующих шагах:
- Определение k-средних начинается с определения позиции \(k\) (здесь, 3) начальных случайных центроидов.
- Затем алгоритм анализирует признаки для каждого наблюдения. Основываясь на используемой мере расстояния, k-средние назначают каждое наблюдение своему ближайшему центроиду, который определяет кластер.
- Затем, используя наблюдения в каждом кластере, k-средние вычисляют новые (\(k\)) центроиды для каждого кластера, где центроид является средним значением включенных в кластер наблюдений.
- Затем k-средние переназначают наблюдения в новые центроиды, переопределяя кластеры с точки зрения включенных и исключенных наблюдений.
- Процесс пересчета новых (\(k\)) центроидов для каждого кластера повторяется.
- Затем k-средние переназначают наблюдения в пересмотренные центроиды, снова переопределяя кластеры с точки зрения наблюдений, которые включены и исключены.
Алгоритм k-средних будет продолжать итерацию до тех пор, пока не прекратится переназначение наблюдений в новый кластер (т.е., пока не будет необходимости пересматривать новые центроиды).
Затем алгоритм завершается, формируя окончательные k-кластеры с их наблюдениями-членами.
Алгоритм k-средних имеет минимизированное внутрикластерное расстояние (тем самым максимизируя единство) и имеет максимизированное межкластерное расстояние (тем самым максимизируя разделение), в соответствии с ограничением (\(k=3\)).
Иллюстрация 20. Пример алгоритма кластеризации с 3-средними.
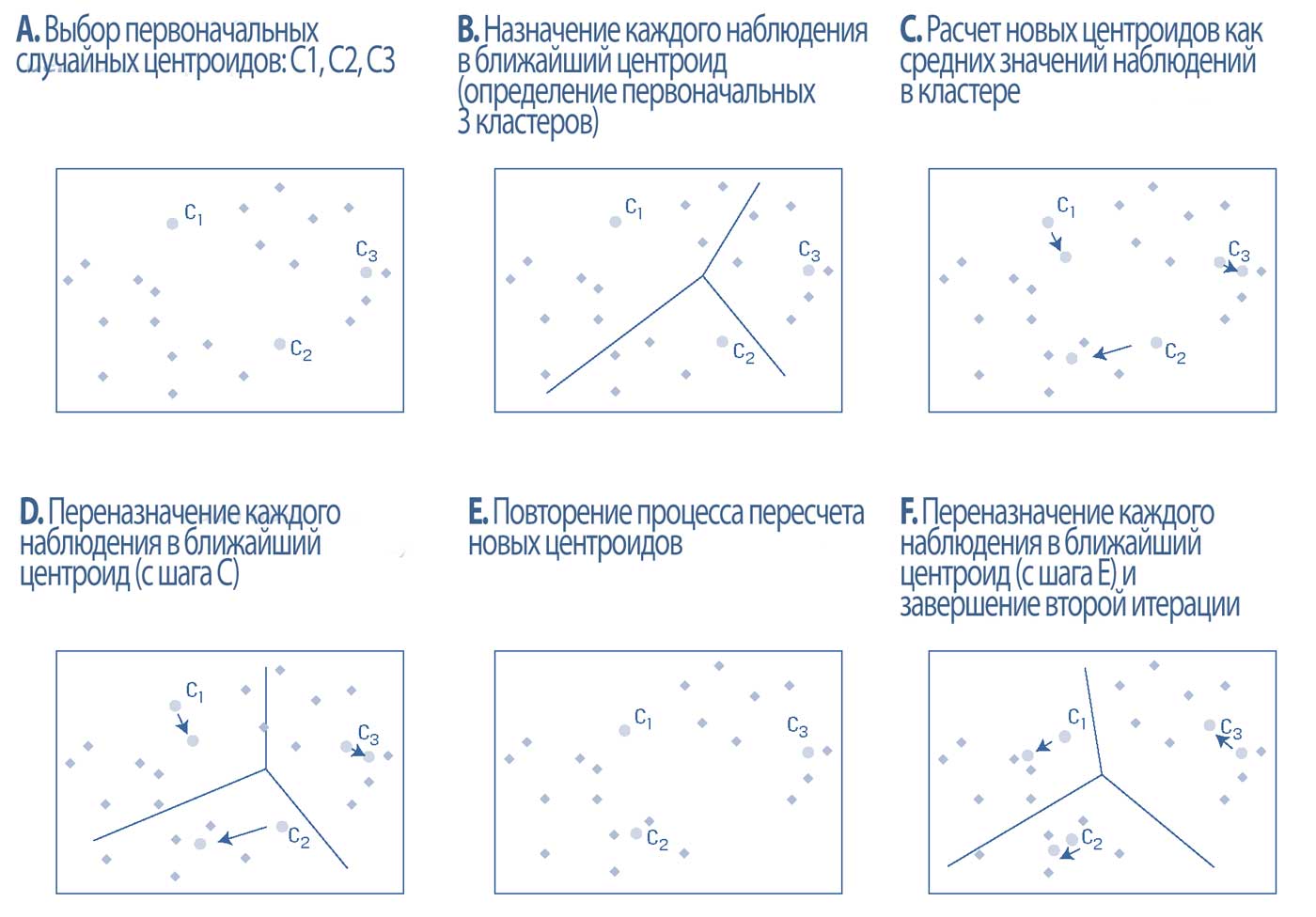
Пример алгоритма с 3-средними.
Алгоритм k-средних быстро и хорошо работает с очень большими наборами данных, включающих сотни миллионов наблюдений.
Однако окончательное назначение наблюдений в кластеры может зависеть от начального местоположения центроидов.
Чтобы решить эту проблему, алгоритм можно запускать несколько раз с использованием различных наборов начальных центроидов, а затем можно выбрать кластеризацию, которая наиболее полезна, с точки зрения бизнес-цели.
Одним из ограничений этого метода является то, что гиперпараметр (\(k\)), количество кластеров, в которых можно распределить данные, необходимо установить до запуска алгоритма k-средних.
Таким образом, нужно иметь представление о том, какое количество кластеров будет обоснованным для исследуемой проблемы и анализируемого набора данных.
В качестве альтернативы можно запустить алгоритм, используя диапазон значений (\(k\)), чтобы найти оптимальное количество кластеров - значение (\(k\)), которое минимизирует внутрикластерное расстояние и, таким образом, максимизирует внутрикластерное сходство (то есть единство) и максимизирует межкластерное расстояние (то есть разделение).
Тем не менее, обратите внимание, что конечные результаты могут быть субъективными и зависящими от контекста задачи и конкретного обучающего набора.
На практике, окончательный выбор (\(k\)) зависит от убежденности аналитика в том, что кластеры оказались обоснованными и интерпретируемыми.
Принятию этого решения сильно помогает использование сводной информации о центроидах и диапазонах значений, а также использование именованных примеров элементов в каждом кластере.
Например, рассмотрим индекс Russell 3000, который отслеживает 3,000 акций компаний с самой высокой рыночной капитализацией в Соединенных Штатах.
Эти 3,000 акций можно сгруппировать в 10, 50 или даже большее число кластеров, основанных на их финансовых характеристиках (например, размер активов, общая выручка, прибыльность, леверидж) и операционных характеристиках (например, численность персонала, интенсивность R&D).
Поскольку компании с одной и той же стандартной отраслевой классификацией могут иметь очень разные финансовые и операционные характеристики, использование k-средних для получения различных кластеров может дать понимание характера однородной группы.
Как уже упоминалось, точный выбор количества кластеров (\(k\)) будет зависеть от желаемого уровня точности или сегментации.
Кластеризация также может использоваться для классификации коллективных инвестиционных инструментов или хедж-фондов в качестве альтернативы стандартным классификациям.
Анализ с помощью кластеризации также может помочь визуализировать данные и облегчить обнаружение тенденций или выбросов в данных.
В целом, алгоритм k-средних является одним из наиболее часто используемых алгоритмов в инвестиционной практике, особенно для обнаружения моделей в данных с высокой размерностью или в качестве метода получения альтернатив существующим классификациям статичной отрасли.
