CFA - Неконтролируемое машинное обучение и анализ главных компонентов (PCA)
Рассмотрим анализ главных компонентов (PCA), один из алгоритмов неконтролируемого машинного обучения, применяющийся для уменьшения размерности данных, - в рамках изучения количественных методов по программе CFA (Уровень II).
Неконтролируемое обучение (англ. 'unsupervised learning') - это машинное обучение, которое не использует размеченные данные (т.е. не использует целевую переменную). Таким образом, алгоритмы должны сами найти паттерны (закономерности) в данных.
Двумя основными типами алгоритмов неконтролируемого ML, показанных в Иллюстрации 2, являются:
- уменьшение размерности, с помощью анализа главных компонентов и
- кластеризация, которая включает k-средние и иерархическую кластеризацию.
Далее мы последовательно опишем каждый из этих алгоритмов.
Анализ главных компонентов.
Уменьшение размерности (англ. 'dimension reduction') является важным типом неконтролируемого обучения, которое широко используется на практике.
Когда в наборе данных присутствует множество признаков, визуальное представление этих данных или подгонка моделей к данным могут стать чрезвычайно сложными и «шумными» в смысле отражения случайного влияния, специфичного для набора данных.
В таких случаях может потребоваться уменьшение размерности. Уменьшение размерности направлено на то, чтобы представить набор данных со многими, обычно коррелирующими признаками с помощью меньшего набора признаков, который при этом будет по-прежнему успешно описывать данные.
Давно найденным статистическим методом уменьшения размерности является анализ главных компонентов (PCA, principal components analysis). PCA используется для обобщения или преобразования сильно коррелирующих признаков данных в несколько основных (главных), некоррелирующих составных переменных.
Составная переменная (англ. 'composite variable') - это переменная, которая объединяет две или более переменных, которые статистически тесно связаны друг с другом.
Неформально, PCA предполагает преобразование ковариационной матрицы признаков и включает в себя два ключевых понятия: собственные векторы и собственные значения.
В контексте PCA собственные векторы (англ. 'eigenvectors') определяют новые, взаимно некоррелированные составные переменные, которые являются линейными комбинациями исходных признаков. Как вектор, собственный вектор также отражает направление.
С каждым собственным вектором связано собственное значение. Собственное значение (англ. 'eigenvalue') означает долю общей дисперсии в первоначальных данных, которые объясняются каждым собственным вектором.
Алгоритм PCA устанавливает собственные векторы, от самых высоких до самых низких, в соответствии с их собственными значениями, то есть с точки зрения их полезности при объяснении общей дисперсии в начальных данных (мы покажем это далее с использованием точечного графика).
PCA выбирает в качестве первого главного компонента собственный вектор, который объясняет наибольшую долю вариаций в наборе данных (собственный вектор с наибольшим собственным значением).
Второй главный компонент объясняет следующую по величине долю вариации, оставшуюся после первого главного компонента. Этот процесс продолжается таким же образом для третьего, четвертого и последующих главных компонентов.
Поскольку главные компоненты представляют собой линейные комбинации первоначального набора признаков, обычно требуется лишь несколько главных компонентов, чтобы объяснить большую часть общей дисперсии в первоначальной ковариационной матрице признаков.
В Иллюстрации 18 показан гипотетический набор данных с тремя признаками, построенный на графике в трех измерениях вдоль осей X, Y и Z.
Каждая точка данных имеет измерение (x, y, z), и данные должны быть стандартизированы таким образом, чтобы среднее значение каждого ряда данных составляло 0, а стандартное отклонение составляло 1.
Предположим, что был применен алгоритм PCA, выявивший первые два главных компонента, PC1 и PC2.
Перпендикулярная линия, отложенная от каждой точки данных до PC1, показывает вертикальное расстояние между точкой данных и PC1. Она представляет ошибку проекции (англ. 'projection error').
Кроме того, расстояние между каждой точкой данных в направлении, которое параллельно PC1 представляет собой спред (разброс) или изменчивость (дисперсию) данных вдоль PC1.
Алгоритм PCA работает таким образом, что он находит PC1, выбирая линию, для которой сумма ошибок проекции для всех точек данных сводится к минимуму и для которой сумма разброса между всеми данными максимизируется.
Как следствие этих критериев отбора, PC1 является уникальным вектором, который учитывает наибольшую долю дисперсии в первоначальных данных.
Следующая по величине часть оставшейся дисперсии лучше всего объясняется вектором PC2, который находится под прямым углом к PC1 и, таким образом, не коррелирует с PC1.
Теперь точки данных могут быть представлены первыми двумя главными компонентами.
Этот пример демонстрирует эффективность алгоритма PCA в обобщении изменчивости данных и достигнутого в результате уменьшения размерности.
Иллюстрация 18. Первый и второй главные компоненты гипотетического трехмерного набора данных.
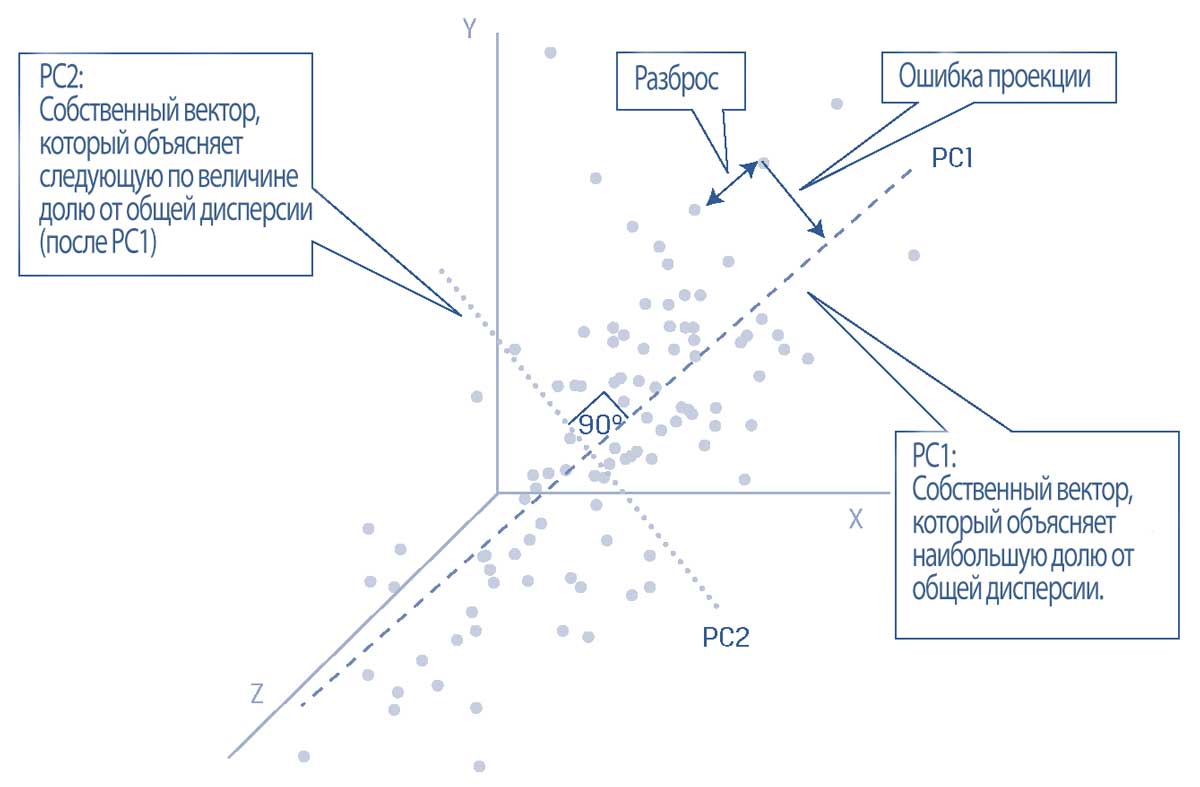
Иллюстрация 18. Первый и второй главные компоненты гипотетического трехмерного набора данных.
Важно знать, сколько главных компонентов следует оставить, потому что существует компромисс между более низкой размерностью, более управляемым представлением сложного набора данных, и некоторой потерей информации.
Scree plots - трехмерные точечные графики, которые показывают долю общей дисперсии в данных, объясненных каждым главным компонентом, могут быть полезны в этом отношении (см. Иллюстрацию 18).
На практике наименьшее количество отобранных главных - это количество, с помощью которого график способен визуально объяснить желаемую долю общей дисперсии в первоначальном наборе данных (часто от 85% до 95%).
Графики для главных компонентов доходности гипотетических рыночных индексов DLC 500 и VLC 30.
В этой иллюстрации исследователи использовали точечные графики и решили, что трех главных компонентов достаточно для объяснения доходности гипотетического индекса акций компаний с большой капитализацией (DLC, Diversified Large Cap) 500 и индекса очень большой капитализации (VLC, Very Large Cap) 30, за последний 10-летний период.
Индекс DLC 500 можно рассматривать как диверсифицированный индекс компаний с большой капитализацией, охватывающих все экономические сектора, в то время как VLC 30 является более концентрированным индексом из 30 крупнейших государственных компаний.
Набор данных состоит из цен на индексы и более чем 2,000 фундаментальных и технических признаков. Мультиколлинеарность среди большого множества признаков является типичной проблемой, потому что многие признаки или комбинации признаков имеют тенденцию перекрывать (частично дублировать) друг друга.
Чтобы смягчить эту проблему, можно использовать PCA для обобщения информации и вариации в данных. Следующие графики показывают, что из 20 сгенерированных главных компонентов первые 3 вместе объясняют около 90% и 86% вариаций в значении индексов DLC 500 и VLC 30 соответственно.
Графики показывают, что для каждого из этих индексов дополнительный вклад в объяснение структуры вариации данных довольно мал после пятого главного компонента.
Следовательно, эти менее полезные главные компоненты можно проигнорировать без большой потери информации.
Графики процентной доли от общей дисперсии, объясненные каждым главным компонентом для гипотетических индексов DLC 500 и VLC 30.
A. Индекс большой капитализации (DLC 500).
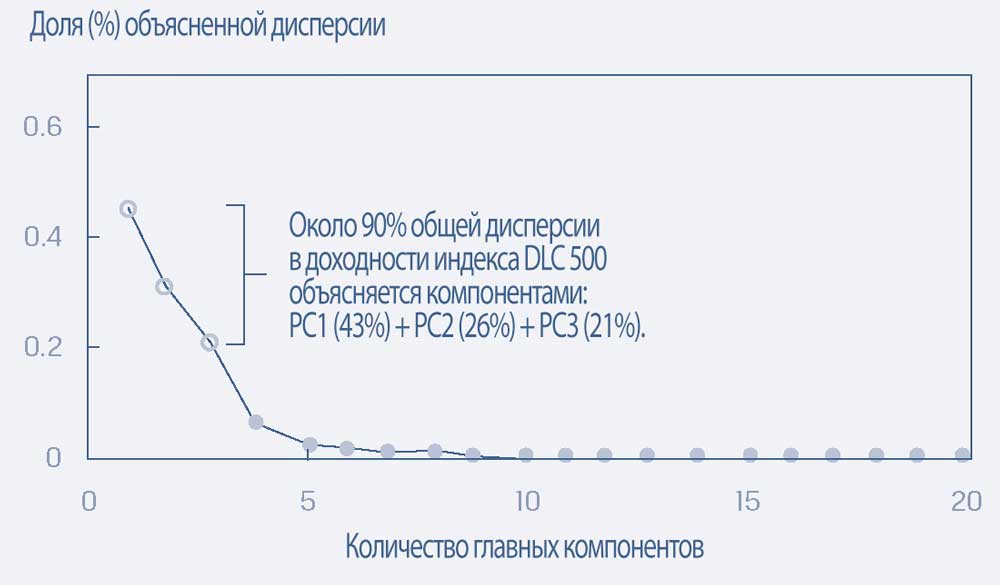
A. Индекс большой капитализации (DLC 500)
B. Индекс очень большой капитализации (VLC 30).
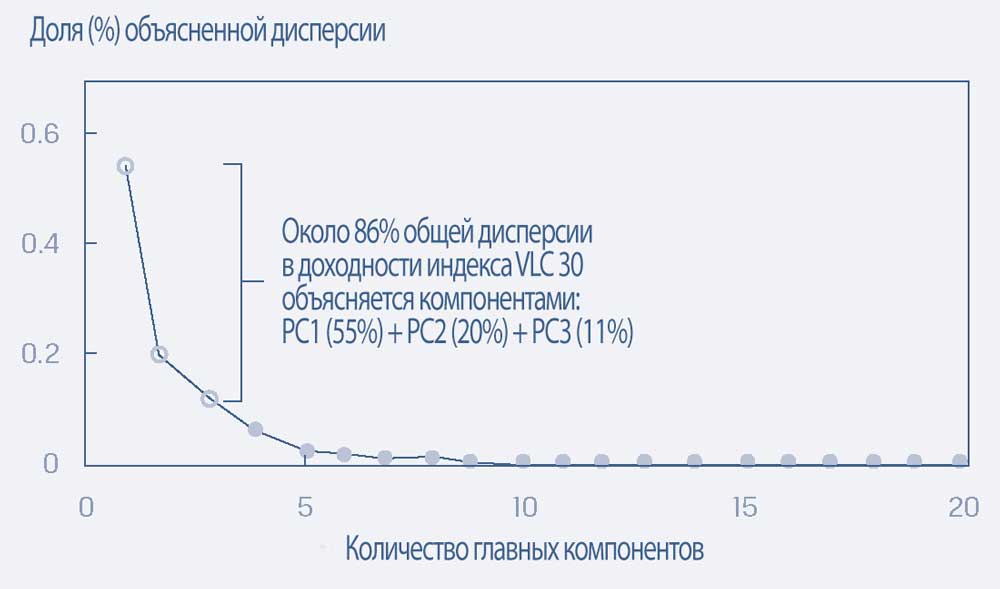
B. Индекс очень большой капитализации (VLC 30)
Основным недостатком PCA является то, что, поскольку главные компоненты являются комбинациями первоначальных признаков, их обычно нелегко разметить или напрямую интерпретировать.
По сравнению с моделированием данных с помощью переменных, которые представляют четко определенные концепции, конечный пользователь PCA может воспринимать PCA как нечто вроде «черного ящика»
Уменьшение количества признаков до наиболее обоснованных предикторов очень полезно, даже при работе с наборами данных, имеющими всего 10 или около того признаков.
Примечательно, что уменьшение размерности облегчает визуальное представление данных в двух или трех измерениях. Обычно его выполняют как часть исследовательского анализа данных, прежде чем обучать другую контролируемую или неконтролируемую модель обучения.
Модели машинного обучения быстрее обучаются, имеют тенденцию к снижению переобучения, и их легче интерпретировать, если они используются для анализа данных с более низкой размерностью.
