CFA - Метод k ближайших соседей (KNN)
Рассмотрим метод k ближайших соседей (KNN), алгоритм контролируемого машинного обучения, - в рамках изучения количественных методов по программе CFA (Уровень II).
Метод k ближайших соседей (KNN, k-nearest neighbor) - метод контролируемого машинного обучения, используемый чаще всего для классификации, а иногда и для регрессии.
Идея этого метода состоит в том, чтобы классифицировать новое наблюдение, обнаружив сходство («близость») между этим новым наблюдением и существующими данными.
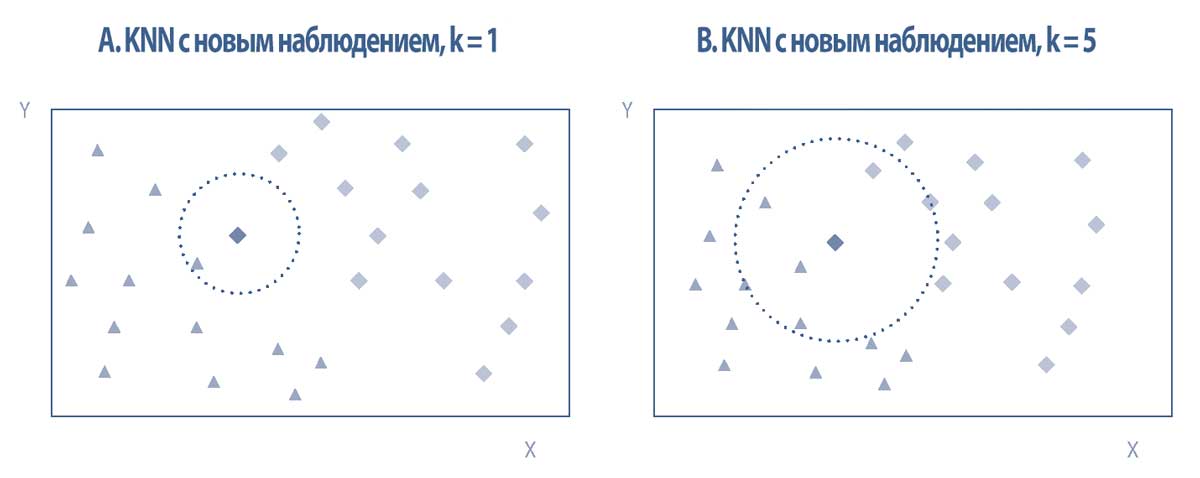
Возвращаясь к точечному графику в Иллюстрации 6, давайте предположим, что у нас есть новое наблюдение: темный ромб в Иллюстрации 8 должен быть классифицирован либо как ромб, либо как треугольник.
Если \(k = 1\), темный ромб будет классифицирован в ту же категорию, что и его ближайший сосед (то есть треугольник на левой панели). Правая панель в Иллюстрации 8 представляет случай, когда \(k = 5\), поэтому алгоритм будет рассматривать пять ближайших соседей темного ромба, которые представляют собой три треугольника и два ромба.
Правило решения состоит в том, чтобы выбрать классификацию с наибольшим количеством ближайших соседей из пяти рассматриваемых наблюдений. Таким образом, темный ромб снова классифицируется как принадлежащий к категории треугольника.
Иллюстрация 8. Алгоритм k ближайших соседей.
Предположим, что у нас есть база данных корпоративных облигаций, классифицированных по кредитному рейтингу, которая также содержит подробную информацию о характеристиках этих облигаций.
Здесь признаки будут включать в себя характеристики компании-эмитента (например, размер активов, отрасль, коэффициенты левериджа, коэффициенты денежных потоков) и характеристики самого выпуска облигаций (например, тенор, фиксированный / плавающий купон, встроенные опционы).
Теперь предположим, что выпускается новая облигация без кредитного рейтинга. По своей природе корпоративные облигации с аналогичными характеристиками эмитента и выпуска должны иметь аналогичный кредитный рейтинг.
Таким образом, используя KNN, мы можем предсказать подразумеваемый кредитный рейтинг новой облигации на основе сходства ее характеристик с характеристиками облигаций в нашей базе данных.
KNN - это прямая, интуитивно понятная модель, которая по-прежнему остается очень мощной, потому что она непараметрическая. Модель не делает допущений о распределении данных. Кроме того, ее можно использовать непосредственно для мультиклассовой классификации.
Важная проблема KNN, однако, заключается в том, какие наблюдения считать «аналогичными» (т.е. близкими соседями). Помимо выбора признаков, важным решением является метрика расстояния, используемая для моделирования сходства, поскольку неуместная мера будет генерировать плохо работающие модели.
Выбор правильной меры расстояния может быть еще более субъективным для порядковых или категориальных данных.
Например, если аналитик изучает сходство рыночных показателей различных акций, он может рассмотреть возможность использования корреляции между исторической доходностью акций в качестве соответствующей меры сходства.
Знание данных и понимание бизнес-целей анализа являются критическими аспектами в процессе определения сходства.
Результаты KNN могут быть чувствительными к включению не относящихся к делу или коррелирующих признаков, поэтому может потребоваться отбор признаков вручную.
Таким образом, аналитик удаляет менее ценную информацию, чтобы сохранить наиболее актуальную и уместную информацию.
Если все сделано правильно, этот процесс должен генерировать более репрезентативную меру расстояния.
Алгоритмы KNN, как правило, лучше работают с небольшим количеством признаков.
Наконец, число \(k\), гиперпараметр модели, необходимо выбирать с пониманием того, что различные значения \(k\) могут привести к различным выводам.
Например, какое значение \(k\) - 3, 15 или 50 облигаций следует выбрать для прогнозирования кредитного рейтинга облигации без рейтинга?
Если \(k\) - четное число, возможны связи и может отсутствовать четкая классификация.
Выбор слишком маленького значения \(k\) приведет к высокому уровню ошибок и чувствительности к местным выбросам. Если же значение \(k\) будет слишком большим, это сведет на нет концепцию ближайших соседей из-за усреднения слишком большого количества результатов.
На практике можно использовать несколько различных методов для определения оптимального значения \(k\), принимая во внимание количество категорий и то, как они разделяют пространство признаков.
Алгоритм KNN имеет множество применений в инвестиционной отрасли, включая прогноз банкротства, прогноз цен на акции, присвоение кредитного рейтинга корпоративным облигациям, а также создание нестандартных индексов акций и облигаций.
Например, KNN полезен для определения облигаций, которые схожи и которые отличаются, что является важной информацией для создания особого диверсифицированного индекса облигаций.