CFA - Иерархическая кластеризация: агломерация и дендрограммы
Рассмотрим иерархическую кластеризацию, алгоритм неконтролируемого машинного обучения, который создает иерархические связи между кластерами данных, - в рамках изучения количественных методов по программе CFA (Уровень II).
Иерархическая кластеризация (англ. 'hierarchical clustering') - это итеративная процедура, используемая для создания иерархии кластеров.
При кластеризации k-средних алгоритм сегментирует данные на заранее определенное количество кластеров; при этом нет определенных взаимосвязей между полученными кластерами.
Однако при иерархической кластеризации алгоритмы создают промежуточные раунды кластеров увеличенного («агломерация») или уменьшенного («разделение») размера, пока не будет достигнута конечная кластеризация.
Процесс создает связи между раундами кластеров, как предполагает слово «иерархический».
Несмотря на то, что иерархическая кластеризация требует более интенсивных вычислений, чем кластеризация k-средних, она имеет преимущество, позволяющее инвестиционному аналитику изучить альтернативные сегментации данных различной гранулярности (степени разбиения), прежде чем принять решение, какую из них использовать.
Агломеративная кластеризация (англ. 'agglomerative clustering') (или иерархическая кластеризация снизу вверх) начинается с того, что каждое наблюдение рассматривается как собственный кластер данного наблюдения. Затем алгоритм находит два ближайших кластера, определяемые некоторым показателем расстояния (сходства), и объединяет их в один новый более крупный кластер.
Этот процесс повторяется итеративно до тех пор, пока все наблюдения не будут объединены в один кластер. Гипотетический пример того, как агломеративная кластеризация формирует иерархическую схему кластеризации, изображена в верхней части Иллюстрации 21, где наблюдения размечены буквами (от A до K), а круги вокруг наблюдений обозначают кластеры.
Процесс начинается с 11 отдельных кластеров, а затем генерирует последовательность групп. Первая последовательность включает в себя пять кластеров с двумя наблюдениями в каждом, и один кластер с одним наблюдением G. Итого, в общей сложности шесть кластеров.
Затем он генерирует два кластера - один кластер с шестью наблюдениями, и другой - с пятью наблюдениями.
Окончательным результатом является один большой кластер, содержащий все 11 наблюдений. Легко заметить, что этот последний большой кластер включает в себя два основных субкластера, каждый из которых содержит три меньших субкластера.
Иллюстрация 21. Агломеративная и разделительная иерархическая кластеризация.
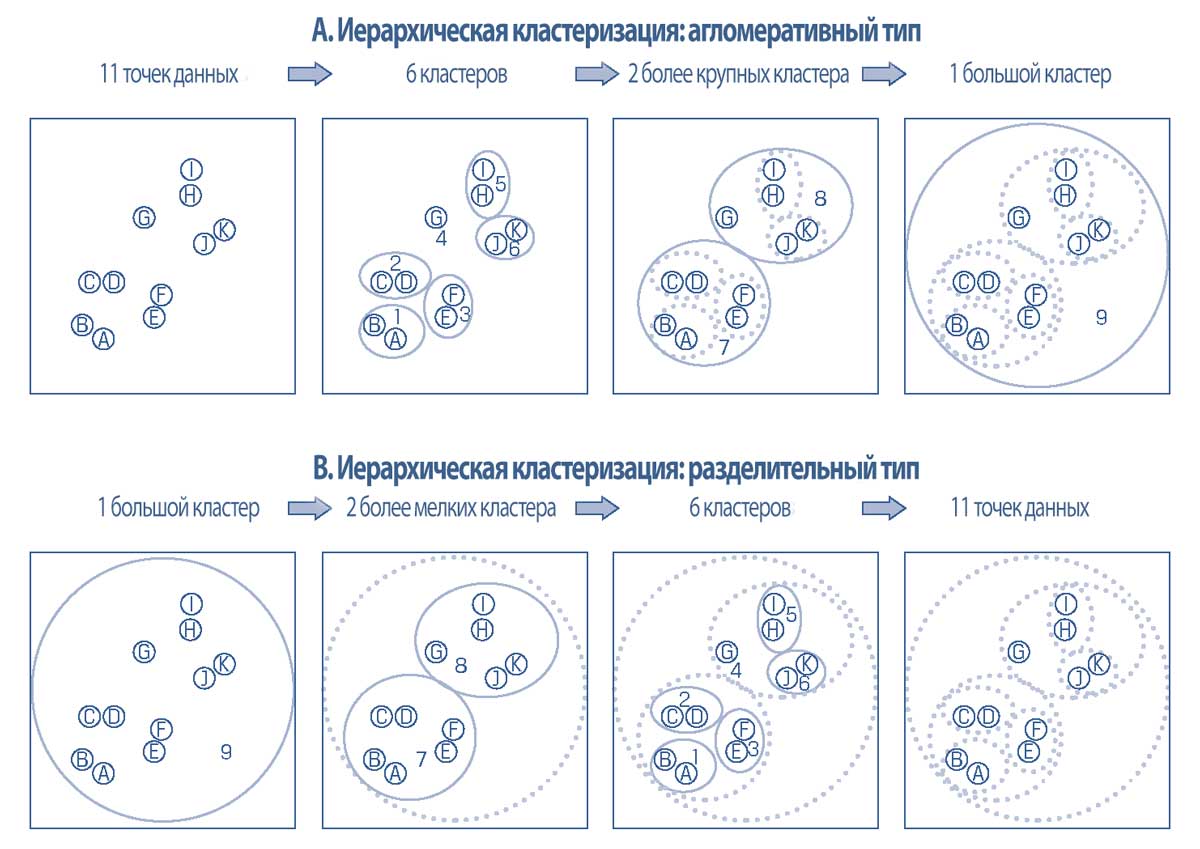
Иллюстрация 21. Агломеративная и разделительная иерархическая кластеризация.
Напротив, разделительная кластеризация (англ. 'divisive clustering') (или иерархическая кластеризация сверху вниз) начинается со всех наблюдений, принадлежащих к одному кластеру.
Затем наблюдения делятся на два кластера на основе некоторой меры расстояния (сходства).
Затем алгоритм постепенно разделяет промежуточные кластеры на более мелкие кластеры, пока каждый кластер не будет содержать только одно наблюдение.
Разделительная кластеризация изображена в нижней части Иллюстрации 21.
Она начинается со всех 11 наблюдений в одном большом кластере.
Затем алгоритм генерирует два меньших кластера, один с шестью наблюдениями, а другой - с пятью наблюдениями; а затем шесть кластеров, с двумя наблюдениями в каждом, за исключением наблюдения G, которое принадлежит собственному кластеру. Наконец, генерируются 11 кластеров, где каждый кластер содержит только одно наблюдение.
Хотя это не является типичным результатом (поскольку два метода обычно используют разные алгоритмы), в этом гипотетическом примере агломеративные и разделительные методы кластеризации дали один и тот же результат: два основных подкластера, каждый из которых включает три меньших подкластера.
Аналитик может сделать выбор между использованием шести- или двухкластерного представления данных.
Агломеративный подход обычно используется с большими наборами данных из-за быстрой вычислительной скорости алгоритма.
Алгоритм агломеративной кластеризации принимает решения о кластеризации на основе локальных паттернов (структурных закономерностей) без первоначального учета глобальной структуры данных.
Таким образом, агломеративный метод хорошо подходит для выявления небольших кластеров.
Однако, поскольку разделительный метод начинается с целостного представления данных, алгоритм разделительной кластеризации предназначен для учета глобальной структуры данных и, следовательно, лучше подходит для определения больших кластеров.
Чтобы принять решение об объединении ближайших кластеров в агломеративном процессе или о разделении в процессе разделения, требуется явное определение расстояния между двумя кластерами.
Некоторые аналитики обычно определяют расстояние между двумя кластерами с помощью поиска минимального, максимального или среднего расстояния между всеми парами наблюдений в каждом кластере.
Дендрограммы.
Тип древовидной схемы, использующейся для визуализации иерархического кластерного анализа, известен как дендрограмма (англ. 'dendrogram'). Дендрограмма подчеркивает иерархические связи между кластерами.
Иллюстрация 22 содержит представление кластеризации, показанной в Иллюстрации 21, в виде дендрограммы.
Во-первых, есть несколько неочевидных технических моментов, связанных с дендрограммами, которые следует упомянуть. Ось X показывает кластеры, а ось Y указывает на некоторую меру расстояния.
Кластеры представлены горизонтальной линией, аркой, которая соединяет две вертикальные линии, называемые дендритами, где высота каждой арки представляет собой расстояние между двумя рассматриваемыми кластерами.
Более короткие дендриты представляют собой более короткое расстояние (и большее сходство) между кластерами. Горизонтальные пунктирные линии, рассекающие дендриты, показывают количество кластеров, на которые данные разделяются на каждом этапе.
Агломеративный алгоритм начинается в нижней части дендрита, где каждое наблюдение представляет собой свой собственный кластер (от A до K).
Затем агломеративная кластеризация генерирует шесть более крупных кластеров (от 1 до 6).
Например, кластеры A и B объединяются, образуя Кластер 1, а наблюдение G остается внутри собственного кластера, который теперь становится Кластером 4. Перемещение вверх по дендрограмме образует два более крупных кластера, где, например, Кластер 7 включает Кластеры от 1 до 3.
Наконец, в верхней части дендрограммы находится общий большой кластер (9). Дендрограмма показывает, что этот самый большой кластер состоит из двух основных субкластеров (7 и 8), каждый из которых имеет три меньших субкластера (от 1 до 3 и от 4 до 6 соответственно).
Дендрограмма также облегчает визуализацию разделительной кластеризации, начиная с верхней части самого большого кластера, а затем двигаясь вниз, пока не будет достигнуто дно дендрограммы, где показаны все 11 кластеров, каждый из которых включает 1 наблюдение.
Иллюстрация 22. Дендрограмма агломеративной иерархической кластеризации.
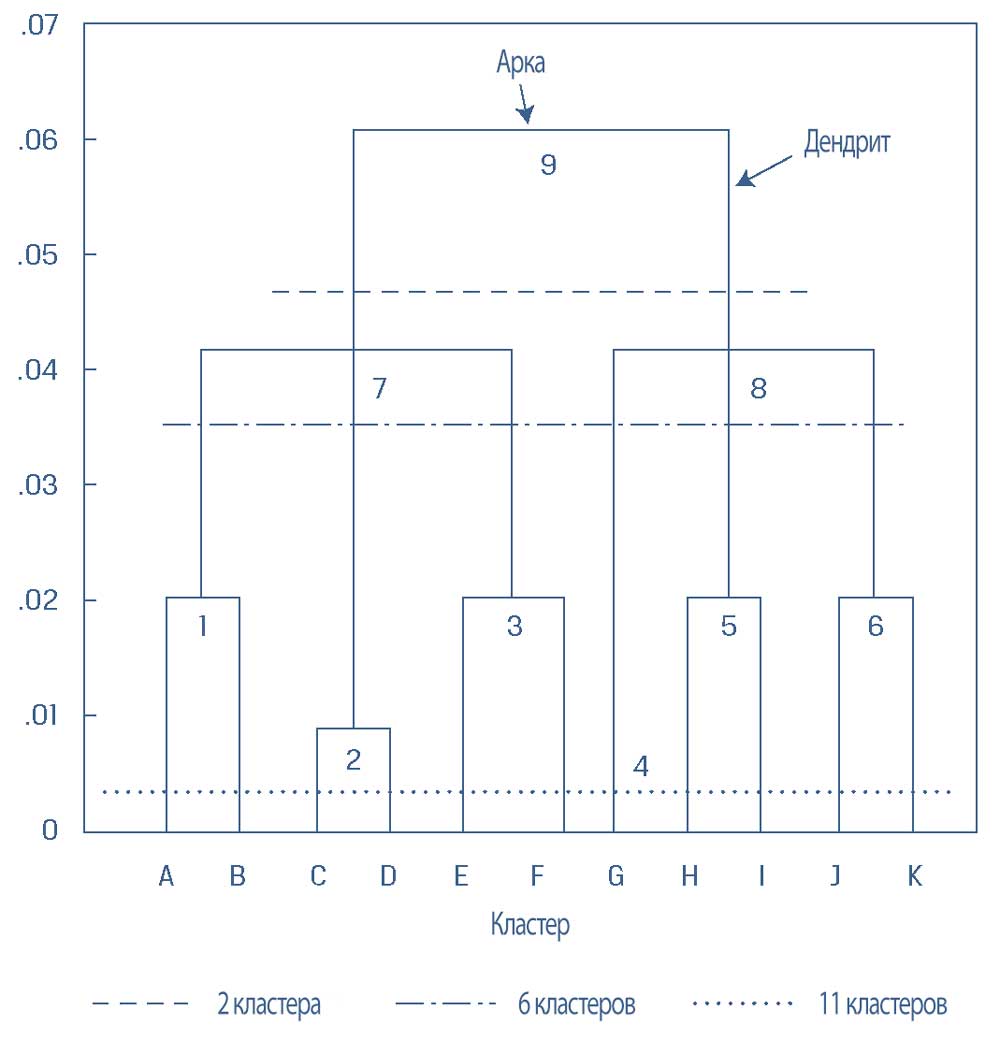
Иллюстрация 22. Дендрограмма агломеративной иерархической кластеризации.
Кластеризация имеет много применений в области управления инвестициями. Например, диверсификация портфеля может рассматриваться как задача кластеризации с целью оптимальной диверсификации рисков путем инвестирования в активы из различных кластеров.
Поскольку кластеры имеют максимальное межкластерное разбиение, диверсификация среди них помогает гарантировать, что портфель отражает широкое разнообразие характеристик и хорошо диверсифицированный риск.
Напротив, информация о том, что инвестиции сосредоточены в одном кластере, указывает на высокую вероятность концентрированного риска.
Наконец, важно отметить, что, хотя результаты алгоритмов кластеризации часто трудно оценить (поскольку сами по себе результирующие кластеры не определены явно), эти алгоритмы все еще очень полезны на практике для раскрытия важной базовой структуры (а именно, сходства между наблюдениями) в сложных наборах данных.
Пример 6. Инвестиционное использование алгоритмов кластеризации.
Истван Переньи является портфельным менеджером Европейского диверсифицированного фонда акционерного капитала («Фонд»), созданного семейной компанией Diversified Investment Management Company (DIMCO).
Доходность Фонда основана на базовом индексе STOXX Europe 600, который охватывает 17 стран, 19 отраслевых секторов и три группы рыночной капитализации (большая, средняя и малая капитализация).
Изучая последние показатели фонда, Переньи был обеспокоен тем, что активы фонда, хотя и приблизительно соответствуют индексу STOXX Europe 600, могут иметь нераспознанные смещения риска и концентрацию.
Переньи попросил Эльзу Лунд, директора по риску, исследовать диверсификацию фонда. Лунд попросила своих аналитиков выдвинуть идеи о том, как можно выполнить запрос Переньи, и получила три предложения:
- Предложение 1. Оцените воздействие риска страны, отрасли и рыночной капитализации на каждый актив фонда, агрегируйте их и сравните совокупное воздействие с воздействием базового индекса STOXX Europe 600. Затем изучите несоответствия, чтобы получить доказательства неожиданных смещений или концентраций.
- Предложение 2. Определите присущие группировки среди фондов на основе широкого набора из восьми числовых показателей (операционных и финансовых), связанных с характеристиками активов. Затем проверьте группировки на наличие доказательств неожиданных смещений или концентраций.
- Предложение 3. Регрессируйте доходность фонда по набору индексов рынка акций страны и индексов сектора, основанных на эталонном индексе фонда. Затем проверьте коэффициенты регрессии на наличие доказательств неожиданных смещений или концентраций.
У Лунд есть несколько вопросов к аналитику Грегу Кейну об использовании одного или нескольких алгоритмов кластеризационного машинного обучения для выполнения запроса Переньи.
Лунд спрашивает, нужно ли определить какую-либо параметры для алгоритмов кластеризации, независимо от того, какой из них используется.
Кейн отвечает, что требуется только мера расстояния, которую будет использовать алгоритм, а также гиперпараметр \(k\) для кластеризации k-средних.
Далее Лунд спрашивает, будет ли преимущество при использовании кластеризации k-средних, а не иерархической кластеризации. Кейн отвечает, что, по его мнению, иерархическая кластеризация является более подходящим алгоритмом.
1. Какое предложение аналитика, скорее всего, будет реализовано с использованием машинного обучения?
- A. Предложение 1
- B. Предложение 2
- C. Предложение 3
2. Ответ Кейна на первый вопрос Лунд о необходимых параметрах для моделей кластеризации ML:
- A. Правильный.
- B. Не правильный, потому что также требуется указать другие гиперпараметры.
- C. Не правильный, потому что также требуется указать набор признаков для описания меры расстояния, используемой для группировки активов.
3. Лучшее обоснование для выбора Кейном иерархической кластеризации в его ответе на второй вопрос Лунд, состоит в том, что Кейн, скорее всего, учитывает:
- A. Скорость вычисления алгоритмов.
- B. Размерность набора данных.
- C. Необходимо указать гиперпараметр \(k\) для использования алгоритма k-средних.
Решение для части 1:
Ответ B верен. Алгоритм кластеризации машинного обучения можно использовать для реализации Предложения 2.
Ответы A и C неверны, потому что Предложения 1 и 3, соответственно, можно легко рассмотреть с использованием традиционного регрессионного анализа.
Решение для части 2:
Ответ C верен. Помимо меры расстояния и гиперпараметра \(k\) для метода k-средних, в зависимости от того, какой алгоритм кластеризации будет выбран, также необходимо указать набор признаков, который будет использоваться для группировки активов по сходным характеристикам.
Операционные и финансовые характеристики компаний, представленных в портфеле фонда, являются примерами таких признаков.
Решение для части 3:
Ответ C верен. Значение гиперпараметра \(k\), отражающего количество отдельных групп, на которые может быть сегментирован индекс STOXX Europe 600, неизвестно. Аналитик должен указать его заранее.
При использовании иерархического алгоритма, сортировка наблюдений в кластерах будет происходить без какого-либо предварительного ввода параметров аналитиком.
