CFA - Нейронные сети

Революция искусственного интеллекта была в значительной степени обусловлена ​​достижениями в нейронных сетях, алгоритмах глубокого обучения и обучения с подкреплением.

Эти сложные алгоритмы могут решать очень сложные задачи машинного обучения, такие как классификация изображений, распознавание лиц, распознавание речи и обработка естественного языка.

Эти сложные задачи характеризуются нелинейностью и взаимодействием между большим количеством входных признаков. Здесь мы предоставляем обзор этих алгоритмов и их инвестиционных применений.

---

Нейронные сети или просто нейросети (англ. 'neural networks') (которые также называют искусственными нейронными сетями - ANN, artificial neural networks) представляют собой очень гибкий тип алгоритмов машинного обучения, который успешно применяется для решения различных задач, характеризующихся нелинейностью и сложным взаимодействием между признаками.

Нейронные сети обычно используются для классификации и регрессии при контролируемом обучении, но также важны для обучения с подкреплением, что не требует разметки обучающих данных человеком.

В Иллюстрации 28 показана связь между множественной регрессией и нейронными сетями. Панель A представляет собой гипотетическую регрессию для данных с использованием четырех входов (inputs), признаков от \(x_1\) до \(x_4\), и одного выхода (output) - прогнозируемого значения целевой переменной \(y\).

Панель B показывает схематическое представление базовой нейронной сети, которая состоит из узлов (nodes) (кругов), соединенных связями (links) (стрелки, соединяющие узлы).

Нейронные сети имеют три типа слоев:

• входной слой (input layer) - здесь он представлен узлом для каждого из четырех признаков;
• скрытые слои (hidden layer) - здесь происходит обучение сети, и входные данные обрабатываются в обученных сетях; и
• выходной уровень (ouput layer) - здесь он состоит из одного узла для целевой переменной \(y\)), который выводит информацию за пределы сети.

Помимо структуры сети, еще одно важное различие между множественной регрессией и нейронными сетями заключается в том, что узлы в скрытом уровне нейронной сети превращают входные данные нелинейным образом в новые значения, которые затем объединяются в целевое значение.

Например, рассмотрим популярную функцию линейного выпрямителя (ReLU, rectified linear unit), \( f(x) = \max(0, x) \), которая возвращает 0, если входное значение отрицательно; или возвращает входное значение, если входное значение положительно.

В этом случае переменная \(y\) будет равна \(\beta_1\), умноженной на \(z_1\), где \(z_1\) - это максимум \((x_1 + x_2 + x_3)\) или 0, плюс \(\beta_2\), умноженной на \(z_2\), максимум \((x_2 + x_4)\) или 0, плюс \(\beta_3\), умноженной на \(z_3\), максимум \((x_2 + x_3 + x_4)\) или 0, плюс член ошибки.

Иллюстрация 28. Регрессия и нейронные сети (регрессия с трансформированными признаками).

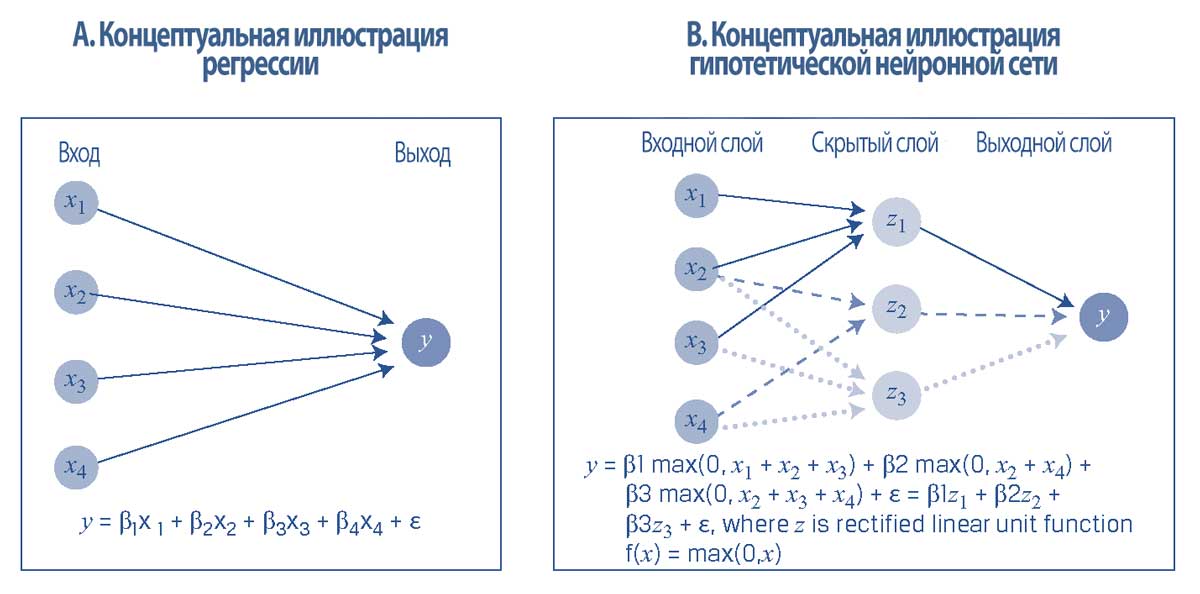
Регрессия и нейронные сети (регрессия с трансформированными признаками).

Обратите внимание, что для нейронных сетей входные признаки будут масштабированы (то есть, стандартизированы) так, чтобы учесть различия в единицах измерения данных.

Например, если входные данные являются положительными числами, то каждую переменную входных данных можно масштабировать по ее максимальному значению так, чтобы трансформированное значение составляло от 0 до 1.

В Иллюстрации 29 показана более сложная нейронная сеть с входным слоем, состоящим из 4 узлов (то есть четырех признаков), одного скрытого слоя, состоящего из 5 скрытых узлов, и 1 выходного узла.

Эти три числа - 4, 5 и 1 - являются для нейронной сети гиперпараметрами, которые определяют структуру нейронной сети.

Иллюстрация 29. Более сложная нейронная сеть с одним скрытым слоем.

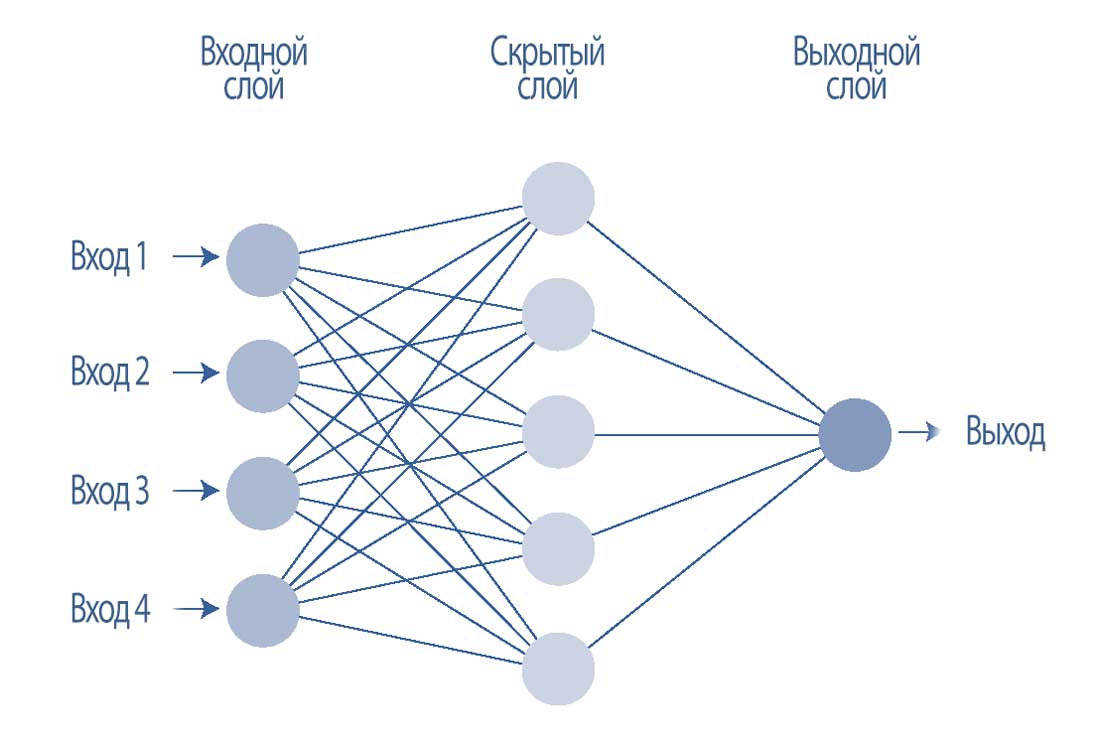
Более сложная нейронная сеть с одним скрытым слоем.

Теперь рассмотрим узлы справа от входного слоя. Эти узлы иногда называют «нейронами» (neurons), потому что они обрабатывают полученную информацию.

Возьмем самый верхний скрытый узел. Четыре связи соединяют этот узел со входами, поэтому этот узел получает четыре значения, передаваемые связями. Каждая связь имеет вес, позволяющий учитывать ее важность (изначально эти веса могут быть назначены случайным образом).

Концептуально, каждый узел имеет две функциональные части: оператор суммирования и функция активации.

 

Как только узел получает четыре входных значения, оператор суммирования (англ. 'summation operator') умножает каждое значение на соответствующий вес, а затем суммирует взвешенные значения, чтобы сформировать общий чистый вход.

Затем общий чистый вход передается в функцию активации (англ. 'activation function'), которая преобразует этот вход в конечный выход узла.

Если описывать образно, функция активации работает как диммерный переключатель света, который уменьшает или увеличивает силу входа.

Функция активации, которая выбирается аналитиком (то есть она является гиперпараметром), нелинейна по своему характеру. Например, это может быть S-образная (сигмоидальная) функция (с выходным диапазоном от 0 до 1) или функция линейного выпрямителя, показанная в Панели B Иллюстрации 28.

Нелинейность подразумевает, что темп изменения выхода отличается на разных уровнях входа.

Эта функция активации показана в Иллюстрации 30, где на левом графике отрицательный общий чистый вход преобразуется с помощью S-образной функции в выход, близкий к 0.

Такое низкое значение выхода подразумевает, что узел не активируется, поэтому в следующий узел ничего не передается. И наоборот, на правом графике положительный общий чистый вход преобразуется в выход, близкий к 1, поэтому узел активируется.

Затем выход из функции активации передается в следующий набор узлов, если есть второй скрытый слой или, как в нашем случае, в узел выходного уровня в качестве прогнозируемого значения.

Только что описанный процесс передачи входов через нейросеть (см. направленные вперед стрелки в Иллюстрации 29), называется прямым распространением (forward propagation).

Иллюстрация 30. Функция активации работает как «диммерный переключатель света» в каждом узле в нейронной сети.

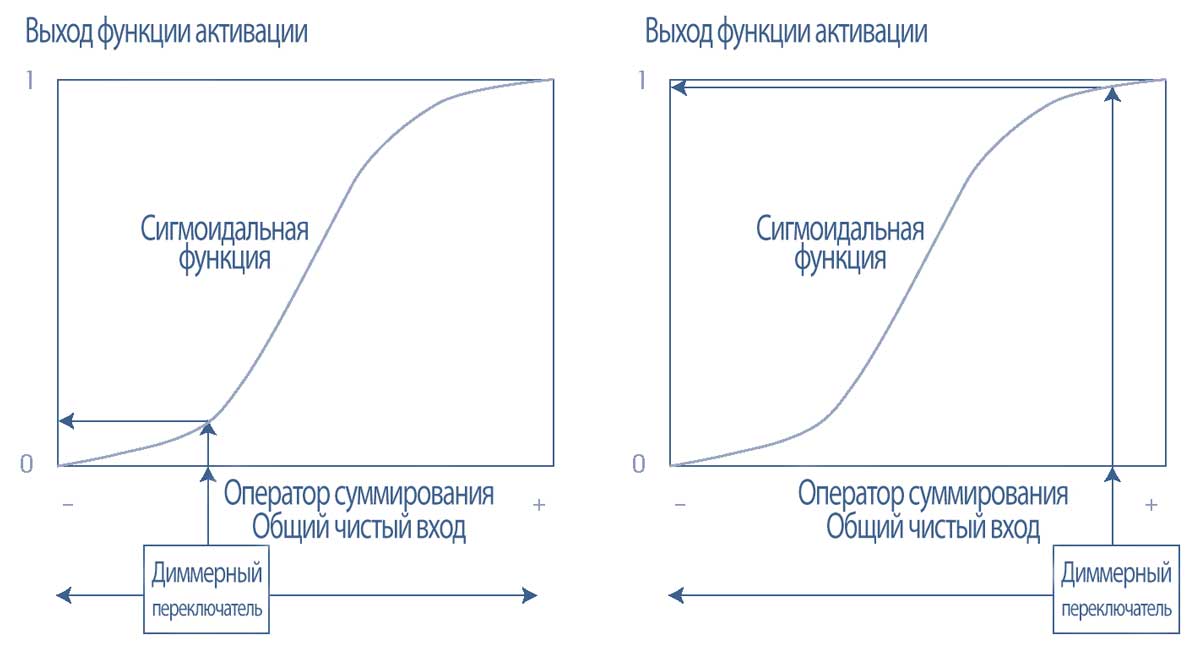
Функция активации работает как «диммерный переключатель света» в каждом узле в нейронной сети.

После ввода набора случайных весов (то есть весов, присвоенных каждой связи), начинается обучение нейронной сети в контролируемом контексте. Это обучение - итеративный процесс, в котором прогнозы сравниваются с фактическими значениями размеченных данных, а эффективность прогноза оценивается в соответствии с выбранным показателем (например, в соответствии со среднеквадратической ошибкой).

 

Затем веса сети корректируется, чтобы уменьшить общую ошибку сети. Если процесс корректировки работает в обратном направлении через слои сети, этот процесс называется обратным распространением (backward propagation).

Обучение выполняется в рамках этого процесса корректировки весов сети с целью снижения общей ошибки.

Без учета направления распространения, суть обновления весов можно неформально выразить как:

Новый вес = (Старый вес) - (Скорость обучения) \(\times\) (Частная производная общей ошибки относительно старого веса),

где частная производная является градиентом или коэффициентом изменения общей ошибки с учетом изменения старого веса и скорости обучения (learning rate). Частная производная является гиперпараметром, который влияет на величину корректировок.

Когда обучение завершается, всем весам сети присваиваются итоговые значения; это параметры сети.

Структура сети, в которой все признаки взаимосвязаны с нелинейными функциями активации, позволяет нейронным сетям раскрывать и аппроксимировать сложные нелинейные связи между признаками.

Вообще говоря, когда указывается больше узлов и больше скрытых слоев, способность нейронной сети справляться со сложностью имеет тенденцию увеличиваться (но при этом также растет риск переобучения).

Ценообразование активов - это шумный, стохастический процесс с потенциально нестабильными связями, который бросает вызов процессам моделирования, поэтому исследователи задаются вопросом, может ли машинное обучение улучшить наше понимание того, как работают рынки.

Исследования, сравнивающие способность статистических методов и методов машинного обучения объяснять и прогнозировать цены на акции до сих пор указывали на то, что простые нейронные сети производят модели доходности акций (на уровне отдельных акций и портфелей), которые превосходят модели, созданные с использованием традиционных статистических методов из-за их способности использовать динамические и взаимодействующие переменные.

Это говорит о том, что модели на основе машинного обучения, такие как нейронные сети, могут просто лучше справляться с нелинейными связями, присущими ценам на ценные бумаги.

Тем не менее, компромиссы при использовании нейронных сетей - это невозможность их интерпретации (то есть, это «черный ящик»), а также большие объемы данных и высокая интенсивность вычислений, необходимые для обучения таких моделей.

Таким образом, нейронные сети могут не подойти для многих инвестиционных применений.