CFA - Этап исследования данных в проектах больших данных

Исследование данных (data exploration) является важной частью проектов больших данных. Подготовленные данные исследуются с целью изучить и понять распределения и взаимосвязи данных.

Знание данных, полученное на этом этапе, используются на протяжении всего проекта больших данных. Результат и качество изучения данных сильно влияют на результаты обучения модели машинного обучения.

Область знаний (domain knowledge) играет жизненно важную роль в исследовательском анализе, поскольку эта стадия требует сотрудничества между аналитиками, дизайнерами моделей и экспертами в конкретной области данных.

Исследование данных без знания области может привести к определению ложных связей между переменными в данных, что в свою очередь может привести к вводящему в заблуждение анализу.

Этап исследования данных следует за этапом подготовки данных и приводит к этапу обучения модели.

Исследование данных включает в себя три важные задачи:

Эти три задачи показаны в Иллюстрации 13. Далее мы подробно рассмотрим эти задачи, а также их особенности и методы при работе со структурированными и неструктурированными данными.

Иллюстрация 13. Стадия исследования данных в проекте больших данных.

Стадия исследования данных в проекте больших данных.

Исследовательский анализ данных (EDA, exploratory data analysis) является предварительным шагом в исследовании данных. Исследовательские графики, диаграммы и другие способы визуализации, такие как тепловые карты и облака слов, предназначены для обобщения и изучения данных.

На практике многие исследовательские графики можно быстро построить с помощью статистических программ и инструментов электронных таблиц.

Данные также можно обобщить и изучить с использованием количественных методов, таких как описательная статистика и меры центральной тенденции.

Важная цель EDA заключается в том, что она служит коммуникационной средой между заинтересованными сторонами проекта, включая бизнес-пользователей, экспертов в данной области знаний и аналитиков.

Относительно быстрые и простые способы исследовательской визуализации помогают заинтересованным сторонам подключаться к проекту и обеспечивать обоснованность подготовленных данных.

Другие цели EDA включают:

• понимание свойств данных,
• поиск закономерностей и взаимосвязей в данных,
• проверку основных вопросов и гипотез,
• документирование распределений данных и других характеристик, а также
• планирование стратегий моделирования для следующих этапов проекта.

Выбор признаков (feature selection) - это процесс, при котором выбираются только нужные признаки из набора данных, предназначенного для обучения модели машинного обучения. Выбор меньшего количества признаков уменьшает сложность модели и время обучения.

Разработка признаков (feature engineering) - это процесс создания новых признаков путем изменения или преобразования существующих признаков. Эффективность модели сильно зависит от выбора и разработки признаков.

Исследование структурированных данных.

Исследовательский анализ данных (EDA).

Для структурированных данных каждая строка таблицы данных содержит наблюдение, а каждый столбец содержит признак. EDA может быть выполнен для одного признака (одномерный) или нескольких признаков (многомерный).

Для сильно многомерных данных со множеством признаков, EDA можно облегчить с помощью метода уменьшения размерности, такого как анализ главных компонентов (PCA).

В зависимости от количества измерений, исследовательские методы будут варьироваться.

Для одномерных данных можно рассчитать сводные статистические показатели, такие как среднее арифметическое, ​​медиана, квартили, размах (интервал изменения), стандартное отклонение, асимметрия и эксцесс.

Одномерная визуализация обобщает каждый признак в наборе данных. Основные способы одномерной исследовательской визуализации следующие:

Гистограммы (histograms) представляют равные интервалы данных и их соответствующие частоты (т.е. количество значений в интервале). Гистограммы можно использовать, чтобы понять распределения данных высокого уровня.

Столбчатые диаграммы (bar charts) суммируют частоты категориальных переменных.

Диаграмма размаха (box plot), известная также как коробчатая диаграмма, усиковая диаграмма или ящик с усами, показывает распределение непрерывных данных, отмечая медиану, квартили и выбросы признака, который соответствует нормальному распределению.

Графики плотности (density plots) являются еще одним эффективным способом понять распределение непрерывных данных. Графики плотности представляют собой сглаженные гистограммы и их обычно помещают поверх гистограмм, как показано в Иллюстрации 14.

Эта гистограмма показывает гипотетическое годовое распределение заработной платы (в £) аналитиков начального уровня в британских банках. Данные представляют собой нормальное распределение с приблизительным средним значением £68,500.

 

Иллюстрация 14. Гистограмма с наложением графика плотности.

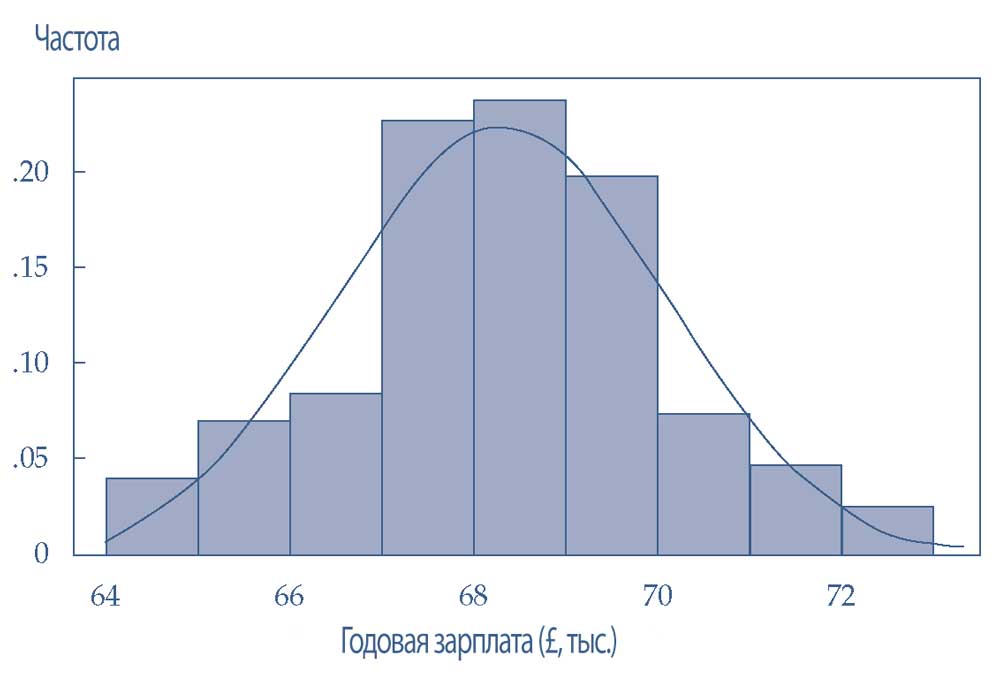
Гистограмма с наложением графика плотности.

Для данных с двумя или более измерениями можно рассчитать сводную статистику взаимосвязей, такую как корреляционная матрица.

Визуализация двух и большего числа измерений исследует взаимодействие между различными признаками в наборе данных.

Общие методы включают в себя графики рассеивания (разброса) и линейные графики. На графики многомерной визуализации накладываются одномерные графики, обобщающие каждый признак, что позволяет сравнить признаки между собой.

Кроме того, можно творчески использовать атрибуты (например, цвет, форма и размер) и подписи, чтобы показать на графиках больше информации о данных.

При исследовании данных обычно используют определенные конструкции из графиков многомерной визуализации. Например, штабельные диаграммы (stacked bar charts) и линейные графики, диаграммы размаха и диаграммы рассеяния, на которых каждый признак выделяется определенным цветом или формой.

Несколько диаграмм размаха можно расположить на одном графике, где каждая диаграмма размаха представляет собой признак. Такой график оценивает взаимосвязь между каждым признаком (ось X) в наборе данных и представляющей интерес целевой переменной (ось Y).

В Иллюстрации 15 график размаха показывает количество приобретенных акций по сравнению с ценой акции (для гипотетической акции). Ось X показывает цену акций с шагом $0.125, а ось Y показывает количество купленных акций.

Отдельные диаграммы (коробки) на графике размаха указывают на распределение акций, приобретенных по различным ценам.

 

Иллюстрация 15. Множественная диаграмма размаха.

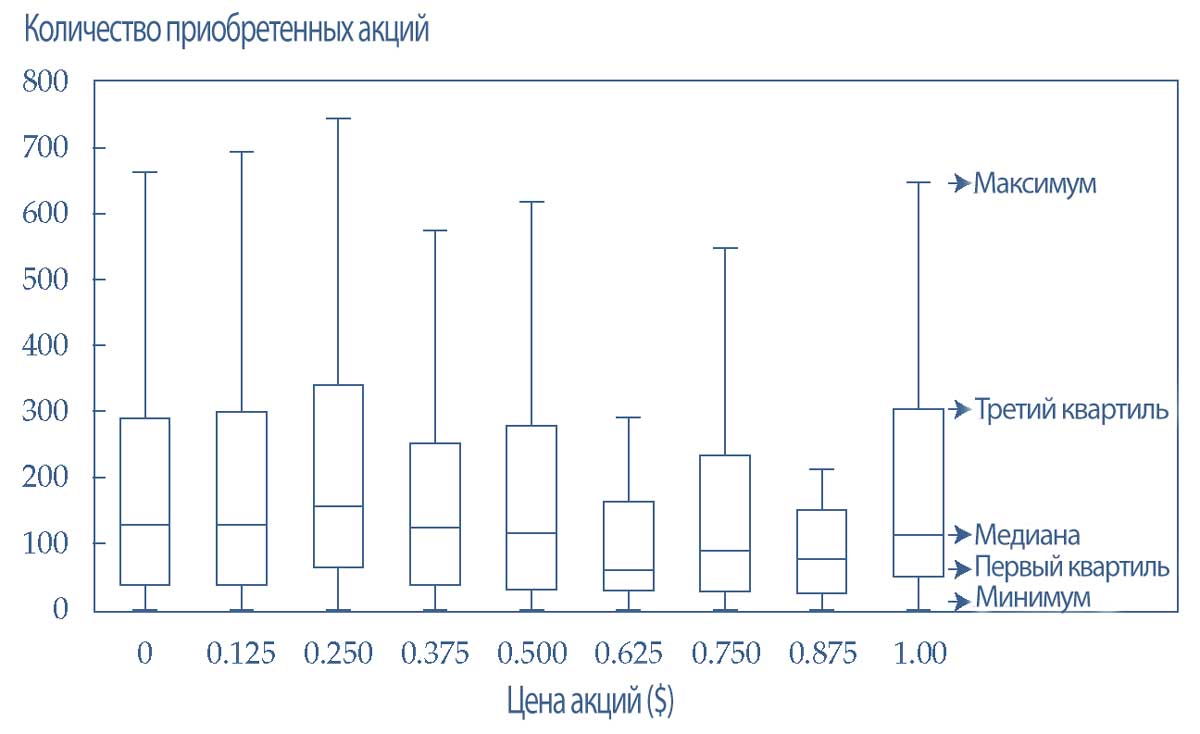
Множественная диаграмма размаха

Двумерные диаграммы могут суммировать и приблизительно измерять взаимосвязь между двумя или более признаками.

На примере графика рассеяния в Иллюстрации 16 показано взаимодействие двух гипотетических признаков: возраст (ось X) и годовая зарплата (ось Y).

Признак на оси Y имеет тенденцию увеличиваться по мере увеличения признака на оси X. Визуально эта закономерность выглядит правильно; однако она может не быть статистически значимой связью.

Диаграмма рассеяния обеспечивает отправную точку для визуального изучения взаимосвязей. Эти потенциальные взаимосвязи необходимо проверять дальше с использованием статистических тестов.

Общие параметрические статистические тесты включают дисперсионный анализ ANOVA, t-критерий и корреляцию Пирсона.

Общие непараметрические статистические тесты включают критерий хи-квадрат и ранговую корреляцию Спирмена.

Иллюстрация 16. Диаграмма рассеяния, показывающая линейную взаимосвязь между двумя признаками.

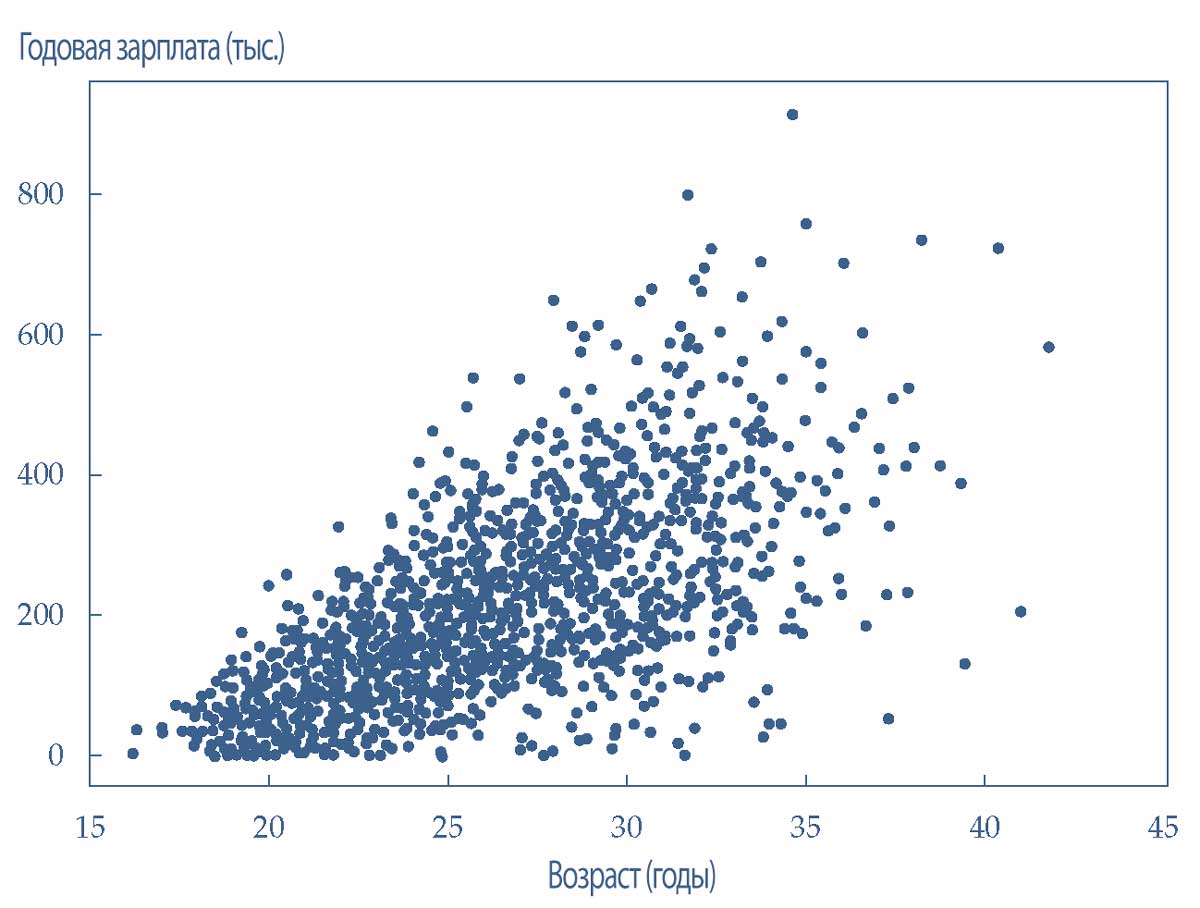
Диаграмма рассеяния, показывающая линейную взаимосвязь между двумя признаками.

В дополнение к визуализации, описательная статистика является хорошим средством обобщения данных. Полезно использовать меры центральной тенденции, а также минимальные и максимальные значения для непрерывных данных.

Чтобы получить представление о распределении возможных значений в категориальных данных обычно используют подсчеты и частоты значений.

Анализ EDA полезен не только для выявления возможных связей между признаками или общих тенденций в данных; он также полезен на этапах выбора и разработки признаков.

Эти возможные связи и тенденции в данных можно использовать, чтобы предложить новые признаки, которые при включении в модель могут улучшить обучение модели.

 

Выбор признаков.

Структурированные данные состоят из признаков, представленных различными столбцами данных в таблице или матрице. После использования EDA для обнаружения соответствующих закономерностей в данных важно идентифицировать и удалить ненужные, необоснованные и избыточные признаки.

Также нужно выполнить базовое диагностическое тестирование признаков, чтобы выявить их избыточность, гетероскедастичность и мультиколлинеарность.

Цель процесса выбора признаков (feature selection) состоит в том, чтобы помочь в определении важных признаков, которые при использовании в модели отражают важные закономерности и сложности более крупного набора данных, в то же время требуя меньше данных в целом.

Эта последняя особенность важна, поскольку вычислительная мощность не является бесплатной (то есть, требуются явные затраты и время обработки).

Как правило, структурированные данные даже после этапа подготовки данных могут содержать признаки, которые не способствуют точности модели машинного обучения или которые негативно влияют на качество обучения модели.

Наиболее желанным результатом является экономная модель с наименьшим количеством признаков, которая при этом обеспечивает максимальную прогностическую силу вне выборки.

Выбор признаков не следует путать с этапами предварительной обработки данных. Хороший выбор признаков требует понимания данных и статистических показателей, а также всеобъемлющего анализа EDA.

Предварительная обработка данных требует разъяснений от администраторов данных и базовой интуиции во время подготовки данных.

Выбор признаков для структурированных данных является методичным и итеративным процессом. Можно использовать статистические показатели, чтобы присвоить балл важности (вес) каждому признаку.

Затем признаки можно ранжировать с использованием этого балла, и затем либо оставить, либо исключить из набора данных. Статистические методы, используемые для этой задачи, обычно являются одномерными и рассматривают каждый признак в отдельности или по отношению к целевой переменной.

Эти методы включают критерий хи-квадрат, коэффициенты корреляции и показатели сбора информации (т.е. коэффициенты детерминации \(R^2\) из регрессионного анализа).

Все эти статистические методы можно объединить таким образом, чтобы каждый метод индивидуально применялся к каждому признаку.

В популярных языках программирования, используемых для создания и обучения моделей машинного обучения, имеются встроенные функции выбора признаков.

Уменьшение размерности помогает определить признаки, которые учитывают наибольшую дисперсию в наблюдениях и позволяют обрабатывать уменьшенный объем данных.

Уменьшение размерности можно применить для уменьшения большого количества признаков, что помогает уменьшить требуемую для вычислений компьютерную память и ускорить выполнение алгоритмов обучения.

Выбор признаков отличается от уменьшения размерности, но оба метода нацелены на уменьшение количества признаков в наборе данных.

Метод уменьшения размерности создает новые некоррелирующие комбинации признаков, тогда как выбор функций включает и исключает признаки, не изменяя их.

 

Разработка признаков.

После выбора подходящих признаков, можно разработать дополнительные признаки - оптимизированные и улучшенные.

Успех обучения модели машинного обучения зависит от того, насколько хорошо данные подготовлены к использованию в модели.

Процесс разработки признаков (feature engineering) пытается создать хорошие признаки, которые описывают структуры, присущие набору данных.

Этот процесс зависит от контекста проекта, области знаний данных и характера задачи.

Структурированные данные, вероятно, будут содержать числовые показатели, разработанные с целью лучшего представления закономерностей в наборе данных. Это действие включает в себя преобразование существующего признака в новый признак или разложение его на несколько признаков.

Для непрерывных данных можно создать новый признак, например, путем получения логарифма из произведения двух или более признаков.

В качестве другого примера, при использовании зарплаты или дохода в качестве признака важно учитывать, что к различным уровням зарплаты применяется разная ставка налогообложения.

Чтобы учесть эту особенность, можно разложить признак дохода на два различных уровня налогообложения путем создания нового признака: «income_above_100k», с возможными значениями 0 и 1.

Значение 1 отражает тот факт, что субъект имеет годовую зарплату более $100,000.

С помощью группировки субъектов по категориям дохода, можно делать допущения о подоходном налоге и использовать их в модели, которая делает финансовые прогнозы с учетом обложения подоходным налогом.

Для категориальных данных новым признаком может быть комбинация (например, сумма или произведение) двух признаков или разложение одного признака на множество других.

Если один категориальный признак представляет уровень образования человека с пятью возможными значениями (высшая школа, ассистент, бакалавр, магистр и докторская степень), тогда эти значения можно разложить на пять новых бинарных признаков, по одному для каждое возможное значение (например, is_highSchool, is_doctorate), которые приобретают значение 0 (false) или 1 (true).

Процесс, при котором категориальные переменные преобразуются в двоичную форму (0 или 1), называется быстрым кодированием в бинарный код (англ. 'one hot encoding'). Это один из наиболее распространенных методов обработки категориальных признаков в текстовых данных.

Когда в данных присутствуют элементы даты и времени, можно разработать такие признаки, как «second of the hour», «hour of the day» и «day of the date», чтобы получить важную информацию об атрибутах временных данных - это важно, например, при моделировании алгоритмов биржевой торговли.

Методы разработки признаков модифицируют, разлагают или объединяют существующие признаки для создания более значимых признаков. Более значимые признаки позволяют модели машинного обучения более быстро и легко обучаться.

Различные стратегии разработки признаков могут привести к получению совершенно разных результатов при использовании одной и той же модели машинного обучения. Влияние выбора и разработки признаков на обучение модели обсуждается в следующем разделе.