CFA - Графическое представление финансовых данных

Графическое отображение данных позволяет нам быстро визуализировать важные характеристики. Например, мы можем увидеть, что частотное распределение имеет симметричную форму, и этот результат может повлиять на то, какое распределение вероятностей мы используем для описания данных.

В этом разделе мы рассмотрим гистограмму, многоугольник частот и накопленное частотное распределение как методы графического отображения данных.

Мы строим все эти графические представления на основе информации, содержащейся в частотном распределении S&P 500 из Таблицы 3 или Таблицы 4 (см. CFA - Обобщение финансовых данных с использованием частотных распределений).

Гистограмма частотного распределения.

Гистограмма является графическим эквивалентом частотного распределения.

Определение гистограммы.

Гистограмма (англ. 'histogram') - это столбиковый график данных, которые были сгруппированы в частотное распределение.

Преимущество визуального отображения заключается в том, что мы можем быстро увидеть, где находится большинство наблюдений. Чтобы увидеть, как строится гистограмма, посмотрите на интервал доходности \(18\% \leq R_t < 20\%\) в Таблице 3. Этот интервал имеет абсолютную частоту 6.

Поэтому мы строим столбец или прямоугольник с высотой 6 для этого интервала доходности на горизонтальной оси графика. Если выполнить тот же процесс для всех остальных интервалов доходности, мы получим гистограмму.

На Рисунке 1 представлена ​​гистограмма годовых ставок доходности S&P 500 с 1926 по 2012 год.

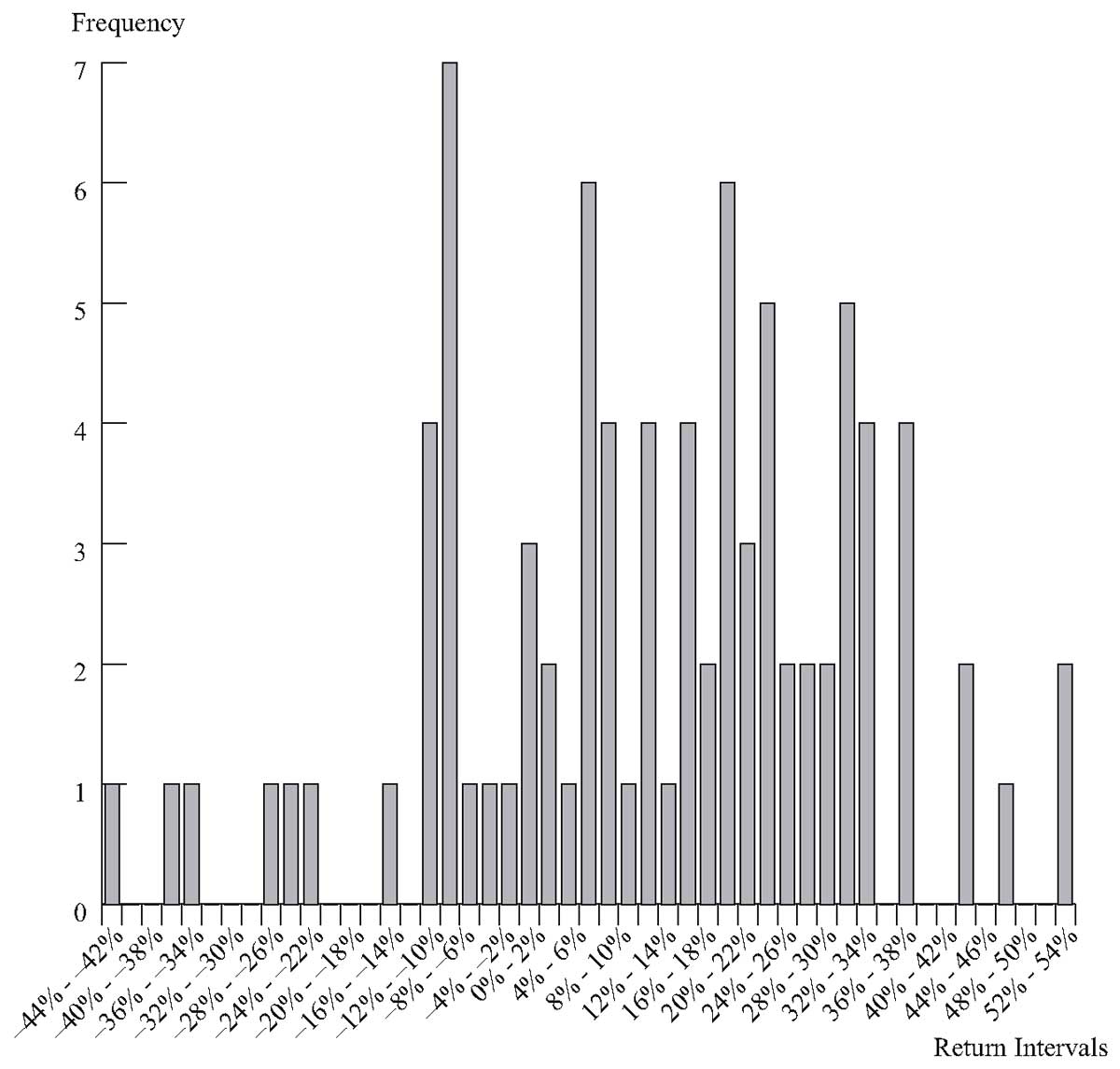Рисунок 1. Гистограмма годовой доходности S&P 500 с 1926 по 2012 год.

Источник: Ibbotson Associates.

Примечание. Из-за ограниченного пространства только каждый второй интервал доходности подписан ниже горизонтальной оси.

На гистограмме на Рисунке 1 высота каждого столбца отражает абсолютную частоту для каждого интервала доходности. Интервал доходности  \(-10\% \leq R_t < -8\%\) имеет частоту 7 и представлен самой высокой полосой на гистограмме.

Поскольку между интервалами нет пропусков, между столбцами гистограммы также нет пропусков. Многие из интервалов доходности имеют нулевую частоту; следовательно, они не имеют высоты в гистограмме.

---

На Рисунке 2 представлена ​​гистограмма для частотного распределения месячной доходности по S&P 500. Она несколько более симметрична, чем гистограмма годовой доходности, показанная на Рисунке 1. Эта гистограмма также выглядит более колоколообразной, чем частотное распределение годовой доходности.

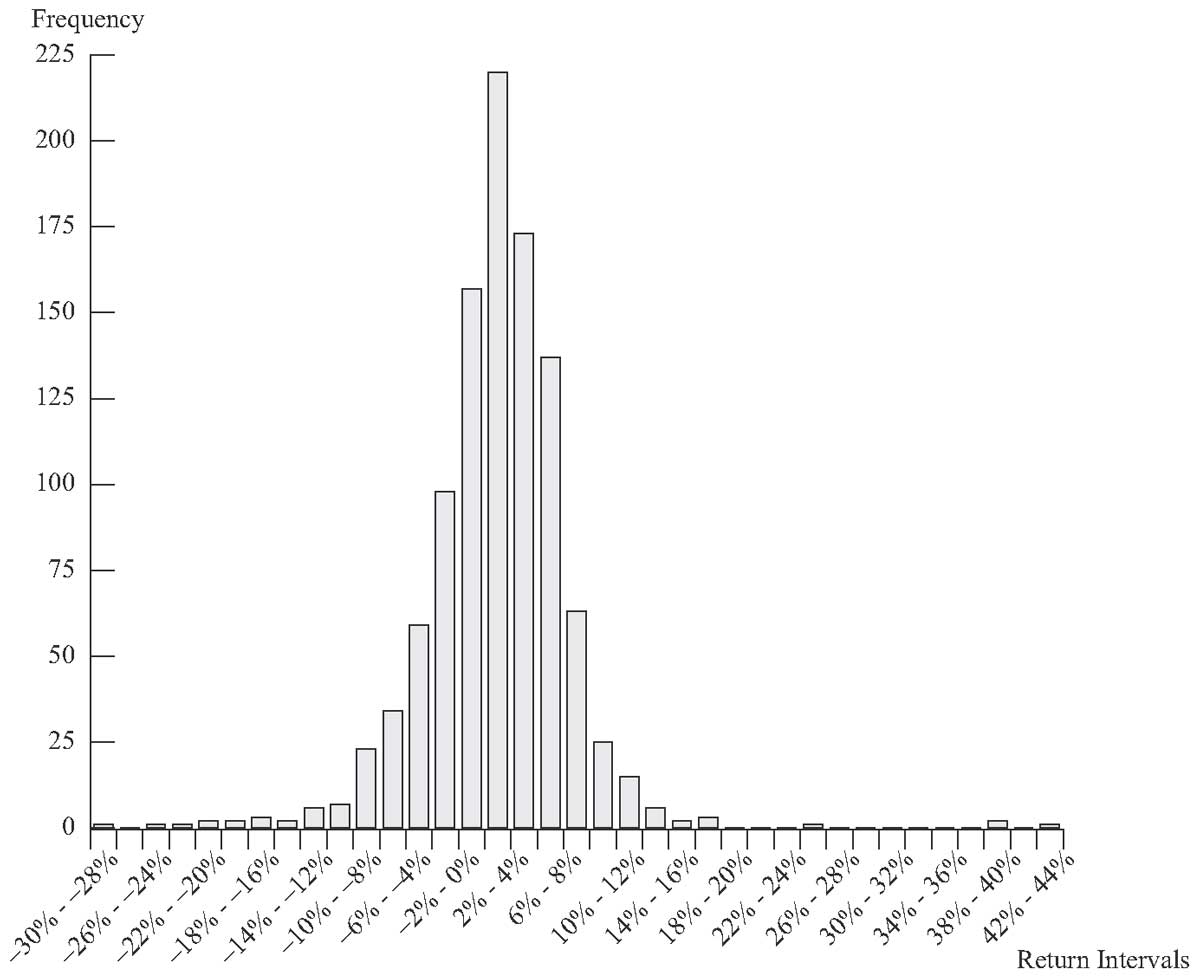Рисунок 2. Гистограмма ежемесячной доходности S&P 500 с января 1926 по декабрь 2012 года.

Источник: Ibbotson Associates.

Многоугольник частот и накопленное распределение частот.

Два других графических инструмента для отображения данных - это многоугольник частот (или полигон частот, от англ. 'frequency polygon') и накопленное распределение частот (англ. 'cumulative frequency distribution').

Чтобы построить многоугольник частот, мы строим среднюю точку каждого интервала на оси \(X\) и абсолютную частоту для этого интервала на оси \(Y\). Затем мы соединяем соседние точки прямой линией.

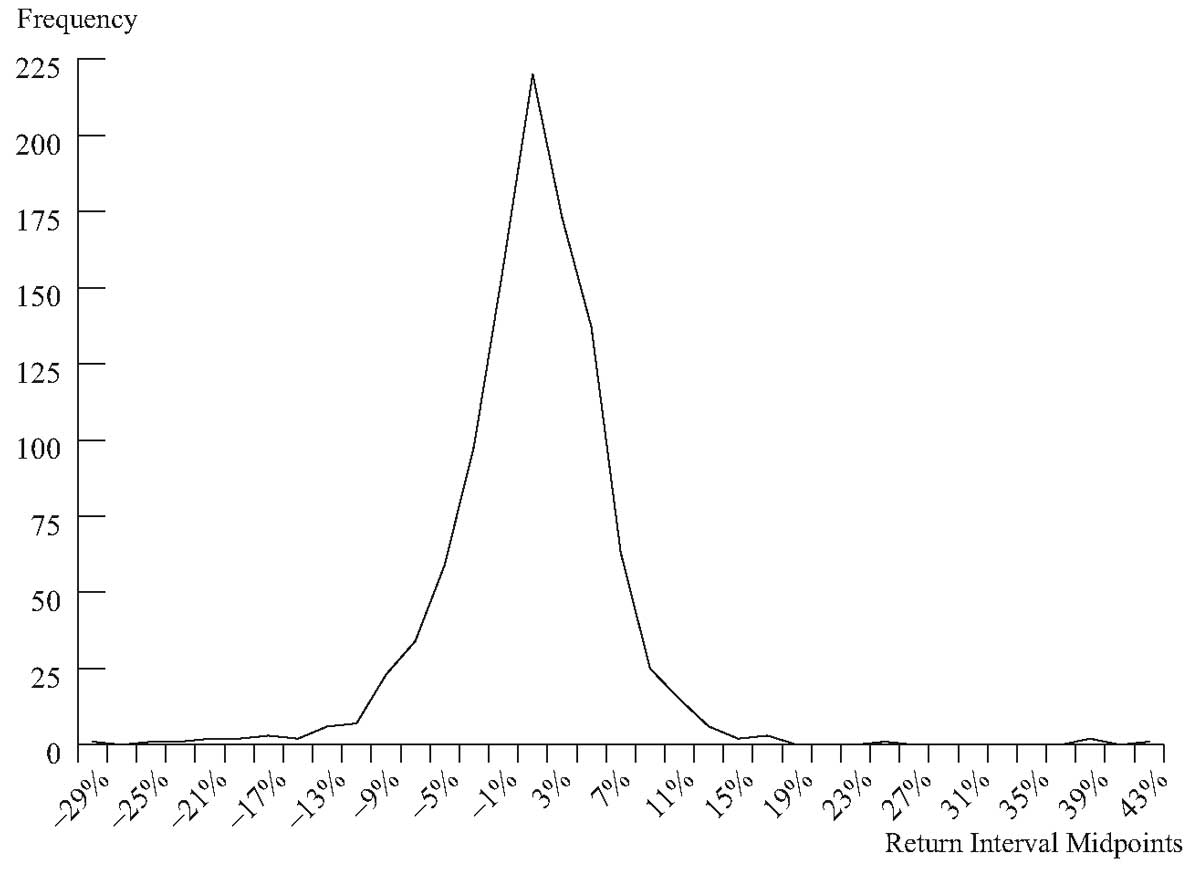
На Рисунке 3 показан многоугольник частот для 1044 месячных ставок доходности S&P 500 с января 1926 года по декабрь 2012 года.

Рисунок 3. Многоугольник частот для ежемесячной доходности S&P 500 с января 1926 по декабрь 2012 года.

Источник: Ibbotson Associates.

На Рисунке 3 мы заменили столбцы гистограммы точками, связанными прямыми линиями. Например, интервал доходности от 0 до 2% имеет абсолютную частоту 220. В многоугольнике частот мы строим среднюю точку интервала доходности в 1% и частоту 220.

Все остальные точки мы строим аналогичным образом. Несмотря на то, что верхний предел интервала не является доходностью, попадающей в интервал, мы по-прежнему усредняем его с нижним пределом, чтобы определить среднюю точку.

Эта форма визуального отображения добавляет степень непрерывности к представлению частотного распределения.

Другой формой линейного графика является накопленное распределение частот. Этот график может отображать либо накопленную абсолютную, либо накопленную относительную частоту в зависимости от верхнего предела интервала.

Накопленное распределение частот позволяет нам увидеть, сколько или какой процент наблюдений лежат ниже определенного значения. Чтобы построить накопленное распределение частот, мы строим график показателей доходности из 4-го или 5-го столбца Таблицы 4 относительно верхнего предела каждого интервала доходности.

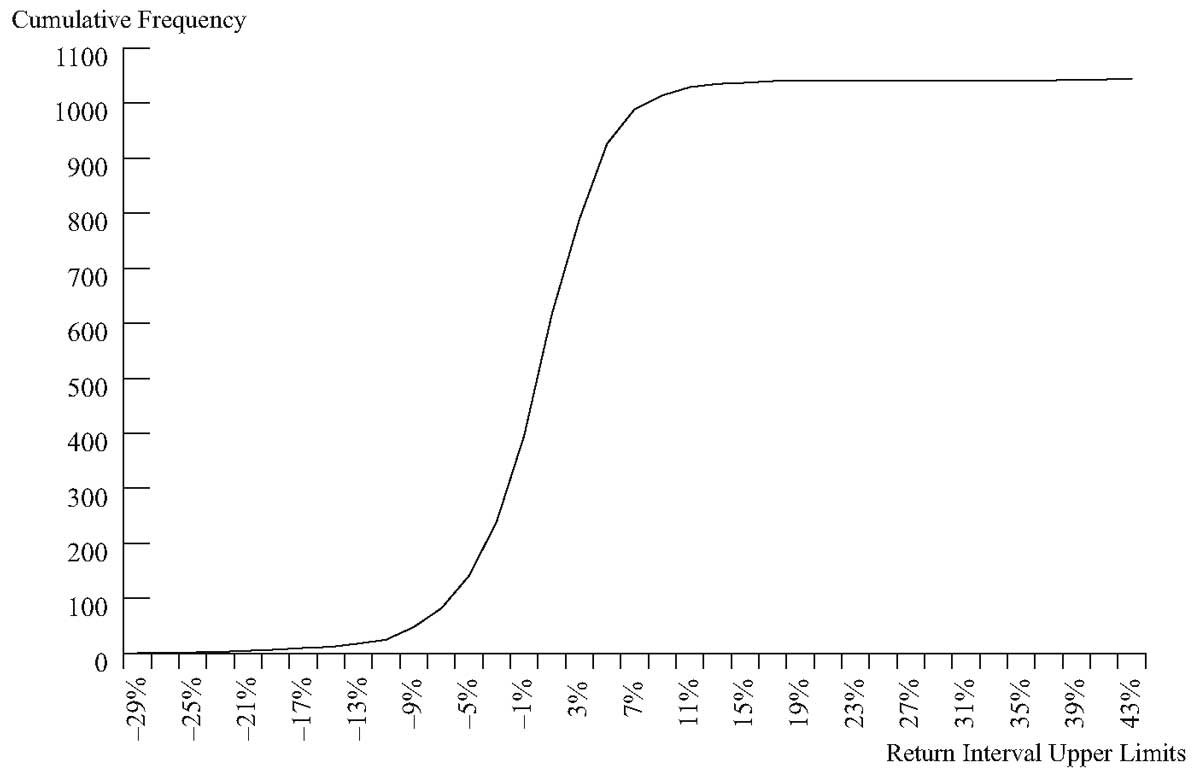
На Рисунке 4 представлен график накопленного абсолютного распределения для ежемесячной доходности S&P 500.

Рисунок 4. Накопленное распределение абсолютной частоты ежемесячной доходности S&P 500 с января 1926 по декабрь 2012 года.

Источник: Ibbotson Associates.

Обратите внимание, что накопленное распределение имеет тенденцию к выравниванию, когда доходность становится чрезвычайно отрицательной или чрезвычайно положительной. Крутой склон в середине графика отражает тот факт, что большинство наблюдений находятся в пределах от -2 до 6%.

Далее мы можем изучить взаимосвязь между относительной частотой и накопленной относительной частотой, взглянув на два интервала доходности, приведенные в Таблице 7.

Таблица 7. Частоты выбранных интервалов
для ежемесячной доходности S&P 500.

Интервал доходности (%)	Абсолют- ная частота	Относи- тельная частота  (%)	Накоп- ленная абсолют- ная частота	Накоп- ленная относи- тельная частота (%)
0.0 до 2.0	220	21.07	616	59.00
2.0 до 4.0	173	16.57	789	75.57

Первый интервал доходности (от 0 до 2%) имеет накопленную относительную частоту 59%. Следующий интервал доходности (от 2 до 4%) имеет накопленную относительную частоту 75,57%.

Изменение накопленной относительной частоты при переходе от одного интервала к следующему является относительной частотой следующего интервала. Например, при переходе от 1-го интервала доходности (от 0 до 2%) к следующему интервалу доходности (от 2 до 4%) изменение накопленной относительной частоты составляет 75,57% - 59,00% = 16,57%. (Значения в таблице округлены до двух десятичных разрядов.)

Тот факт, что наклон крутой, указывает на то, что эти частоты большие.

Как вы можете видеть на графике накопленного распределения, наклон кривой изменяется при переходе от первого интервала доходности к последнему. Довольно маленький наклон накопленного распределения для первых нескольких интервалов доходности говорит нам о том, что эти интервалы доходности не содержат много наблюдений.

Вы можете вернуться к частотному распределению в Таблице 4 и убедиться, что накопленная абсолютная частота составляет всего 25 наблюдений (накопленная относительная частота составляет 2,39%) вплоть до 10-го интервала доходности (от -12 до -10%).

По сути, наклон накопленного абсолютного распределения на любом конкретном интервале пропорционален количеству наблюдений в этом интервале.